espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > actions nationales 2011-2012
une progression autour de l'algèbre en classe de 4ème
mis à jour le 15/05/2013
Dans le cadre des TraAM 2012-2013, une proposition de progression pour aborder l'algèbre en quatrième.
mots clés : TraAM, progression, algebre, gamme, équation, calcul littéral
Ce document, fruit de la réflexion d'un groupe de travail de quatre enseignants de collège n'ambitionne que de proposer un exemple de progression pour l'année de 4ème avec les compétences de calcul littéral et les compétences de résolution de problème comme fil conducteur.
Plusieurs principes ont guidé nos choix et nos propositions :
a) Nous souhaitons que les pratiques pédagogiques, qui peuvent être adoptées pour renforcer la maîtrise calculatoire des élèves, ne soient pas mises en œuvre au détriment des activités de recherche de problèmes. En particulier, l'activité mathématique d'un élève fragile ne doit absolument pas se résumer à l'acquisition de technique calculatoire. Tout élève, y compris le plus fragile, doit prioritairement apprendre à résoudre des problèmes (ouverts).
b) Dans le cadre de la construction de ces nouvelles techniques calculatoires, il est nécessaire de différencier les attendus. Les élèves qui ont du potentiel peuvent avoir un entraînement technique supplémentaire. Ils auront besoin durablement d'une solide maîtrise calculatoire. Par leurs capacités à automatiser certains calculs, à proposer des stratégies de résolution de problèmes nouvelles, les outils numériques sont un bon moyen de différencier la pédagogie.
c) Pour construire des automatismes il faut s'entraîner régulièrement, suffisamment, par petites touches et de façon récurrente, de manière à donner à chaque élève toutes les chances de se les approprier. On peut donc s'autoriser à travailler la technique même si nous limitons le plus possible le nombre des règles calculatoires données.
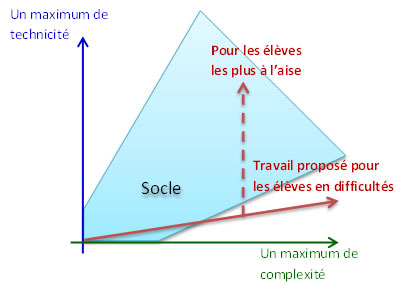 Le schéma ci-contre résume la philosophie de nos travaux avec les élèves :
Le schéma ci-contre résume la philosophie de nos travaux avec les élèves :- Il y a ce que nous considérons comme INCONTOURNABLE : que chaque élève, y compris le plus fragile, soit en activité de résolution de problème.
- Et il y a ce qui nous parait SOUHAITABLE : qu'un élève puisse résoudre un problème pleinement, en utilisant une stratégie experte, et donc souvent algébrique.
Ainsi, les travaux à privilégier pour les élèves fragiles vont vers moins de technicité opératoire et algébrique mais font la part belle à la complexité des problèmes à résoudre (problèmes concrets, problèmes ouverts, taches complexes). Cependant, à aucun moment nous n'oublions que toute situation de recherche est une bonne occasion pour travailler aussi la technique. Et nous ne manquons pas les occasions permettant aux élèves les plus rapides de monter en compétence technique.
Pour la suite, nous avons choisi de décomposer notre document en une progression en 5 temps, qui peuvent correspondre aux 5 périodes de l'année (découpées par les vacances scolaires), mais qui peuvent aussi s'adapter aux progressions spiralées permettant car la construction des compétences et des techniques algébriques méritent un enseignement « par petites touches et de façon récurrente ».
Au sujet du programme et des travaux algébriques de la classe de quatrième
Le programme - Le socle Pratiques et remarques Enjeux pour plus tard
| Le programme - le scocle | Pratiques et remarques | Enjeux pour plus tard | |
| Calcul littéral Manipulations d'écritures littérales | Sur des exemples littéraux, utiliser les égalités k(a + b)= ka + kb et k(a b)= ka kb dans les deux sens. (voir temps 1) Calculer la valeur d'une expression littérale. Tester une égalité. (voir temps 1) Connaître le sens des mots « développer », « réduire », « factoriser » (voir temps 2) Réduire une expression littérale (voir temps 2) Développement de (a+b)(c+d) (voir temps 4) | Veiller à ce que les élèves puissent justifier oralement leurs explications. Etudier pourquoi 2 + 3x ne se réduit pas au contraire de 2x+3x. (voir temps 1) Multiplier les approches de la double distributivité (voir temps 4) | Le calcul littéral sera utilisé dans toutes les classes suivantes mais on veillera à ne pas travailler la technique au détriment de la richesse et de la complexité des situations mathématiques étudiées. On pourra aller plus loin dans les exigences techniques avec les élèves les plus à l'aise. |
| Autour des équations | Mettre en équation et résoudre un problème conduisant à une équation du premier degré à une inconnue. (voir temps 3) Savoir dire si un nombre est solution d'une équation. (voir temps 3) Savoir résoudre une équation du type ax+b = c (voir temps 3), une équation du type ax+b = cx+d (voir temps 5) | Mise en place très progressive, de la cinquième à la seconde de la différence pour l'élève entre égalité et équation. Savoir verbaliser sa démarche. Autoriser tout type de démarche de résolution de ces équations sans s'interdire de travailler des techniques précises (voir temps 3 et 5). | Les équations sont un des moyens très utilisés pour résoudre toutes sortes de problèmes, dans toutes les disciplines scientifiques. On s'attachera cependant à valoriser tout type de démarche de résolution de problème en montrant aux élèves que les méthodes algébriques sont parfois un bon moyen d'être efficace... |
Emmanuel Malgras, Enseignant au collège Pierre et Marie Curie (44 - Le Pellerin)Grégory Maupu, Enseignant au collège Charles Milcendeau (85 - Challans)Stéphane Percot, Enseignant au collège Nicolas Haxo (85 - La Roche-sur-Yon)Yannick Danard, Enseignant au collège Clément Janequin (49 - Avrillé)
information(s) pédagogique(s)
niveau : tous niveaux, 4ème
type pédagogique : non précisé
public visé : enseignant, élève
contexte d'usage : non précisé
référence aux programmes :
ressources associées

|
algebre 4eme temps 1 | 15/05/2013 |
| Dans le cadre des TraAM 2012-2013, une proposition de progression pour aborder l'algèbre en quatrième. | ||
| TraAM, progression, algebre, gamme, équation, calcul littéral | Yannick Danard; Gregory Maupu; Stéphane Percot; Emmanuel Malgras | |

|
algebre 4eme temps 2 | 15/05/2013 |
| Dans le cadre des TraAM 2012-2013, une proposition de progression pour aborder l'algèbre en quatrième. | ||
| TraAM, progression, algebre, gamme, équation, calcul littéral | Stéphane Percot; Grégory Maupu; Emmanuel Malgras; Yannick Danard | |

|
algebre 4eme temps 3 | 15/05/2013 |
| Dans le cadre des TraAM 2012-2013, une proposition de progression pour aborder l'algèbre en quatrième. | ||
| TraAM, progression, algebre, gamme, équation, calcul littéral | Emmanuel Malgras; Yannick Danard; Grégory Maupu; Stéphane Percot | |

|
algebre 4eme temps 4 | 15/05/2013 |
| Dans le cadre des TraAM 2012-2013, une proposition de progression pour aborder l'algèbre en quatrième. | ||
| TraAM, progression, algebre, gamme, équation, calcul littéral | Grégory Maupu; Yannick Danard; Emmanuel Malgras; Stéphane Percot | |

|
algebre 4eme temps 5 | 15/05/2013 |
| Dans le cadre des TraAM 2012-2013, une proposition de progression pour aborder l'algèbre en quatrième. | ||
| TraAM, progression, algebre, gamme, équation, calcul littéral | Grégory Maupu; Emmanuel Malgras; Stéphane Percot; Yannick Danard | |
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA
