espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > actions nationales 2015-2017
marche aléatoire
mis à jour le 26/03/2016
mots clés : algorithmique, TraAM, déplacement, aléatoire
Premiers contacts avec l’algorithmique
Les élèves de 4ème et de 3ème ont déjà eu l’occasion de se confronter à de petites activités mathématiques avec des outils algorithmiques :
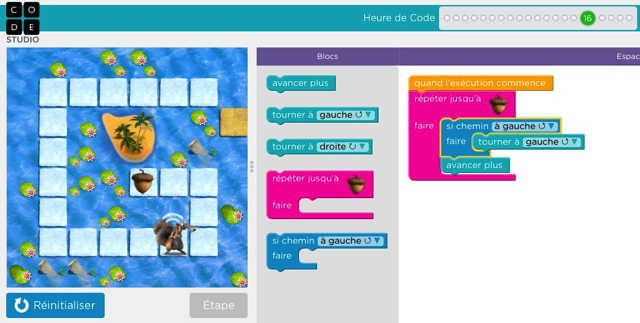
- Dans un premier temps d’initiation, ils avaient utilisé le site « hour of code » (heure de code) : https://studio.code.org/hoc/1 qui propose de résoudre 20 « puzzles » (des labyrinthes) à l’aide de bloc de programmations de déplacements, exactement comme avec l’outil Scratch.
Cet outil en ligne à l’avantage d’introduire de façon très ludique et adaptée à tout âge les éléments nécessaires à la réalisation d’algorithme (déplacements simples, boucles « pour », boucles « jusqu’à », test « si alors sinon… »).
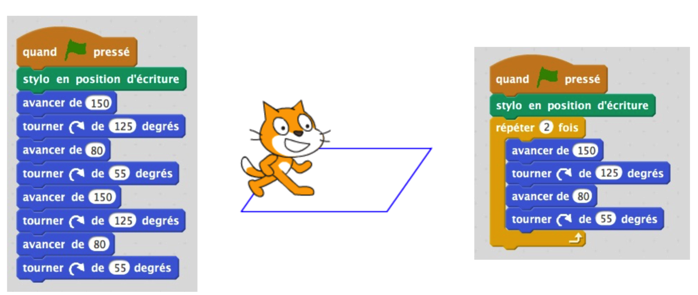
Première marche aléatoire : de bas en haut
Nous sommes en salle multimédia. Deux élèves par poste (je ne peux pas faire autrement… : 15 postes pour 28 élèves). L’interface Scratch qu’ils ont déjà découverte une fois et le fonctionnement des blocs (par glisser-déposer) ne posent pas de souci.
Je propose aux élèves de programmer une marche aléatoire du lutin du bas de l’écran vers le haut de l’écran avec comme consigne qu’à chaque déplacement, que l’on va répéter un grand nombre de fois, le lutin avance « aléatoirement » soit « en diagonale vers la gauche » (orientation à - 45°) soit en « diagonale vers la droite » (orientation à 45°).
Je précise aux élèves que l’opérateur
 pourra être utile et que je les invite à faire fonctionner plusieurs fois leur programme pour en observer les résultats.
pourra être utile et que je les invite à faire fonctionner plusieurs fois leur programme pour en observer les résultats.Suite à des demandes de précisions des élèves sur la position de départ, nous convenons de placer le lutin en position (0 ; -150) au début du programme… et je laisse ensuite, volontairement, les élèves « bidouiller » un peu et programmer en fonction de leurs envies…
Nous obtenons rapidement des programmes variés mais parfois un peu différent de l’attendu :
Exemple 1 : une marche aléatoire sans utilisation de variable mais avec 3 déplacements possibles :

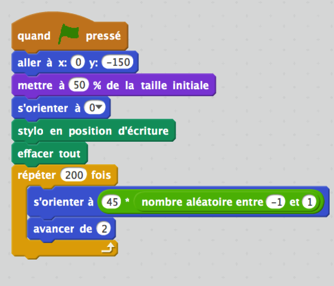
On apprécie ici la simplicité du programme mais on constate qu’il ne correspond pas tout à fait à la consigne : il y a 3 déplacements possibles. Et en rejouant plusieurs fois le programme, on remarque que le lutin ne s’écarte pas beaucoup de l’axe vertical central.
Exemple 2 : une marche aléatoire avec utilisation d’une variable et 2 déplacements possibles :
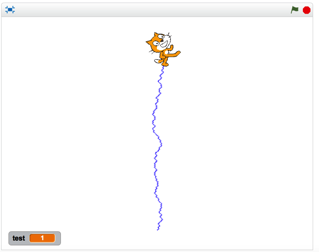
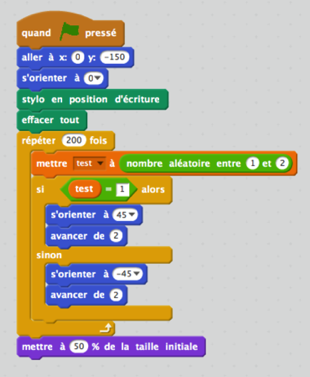
Ce programme n°2 correspond tout à fait à la consigne et l’utilisation de la variable « test » est évoquée lors d’un point collectif.
En rejouant le programme, on remarque des parcours variés de la part du lutin.
Y compris sans effacer les parcours précédents (1ère évolution du programme proposé) :

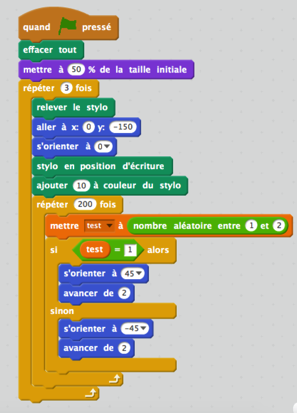
Ici, un groupe d’élève a modifié son programme avec un changement de couleur entre chacun des parcours.
Prolongement : vers un jeu de pari
Je propose aux élèves de compléter leur programme pour en faire un jeu de pari : parier sur le fait que le lutin finira plutôt à gauche ou plutôt à droite de l’écran.
Pour cela, on peur tracer un trait verticale et observer le résultat.
On peut aussi demander à l’utilisateur de parier au départ et tester à la fin du parcours du lutin si le pari est gagnant ou perdant…
Voici quelques programmes obtenus
Jeu 1 : « le trait juste pour voir »
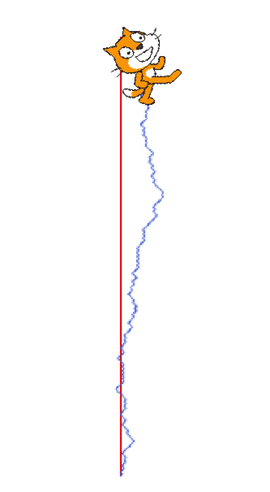
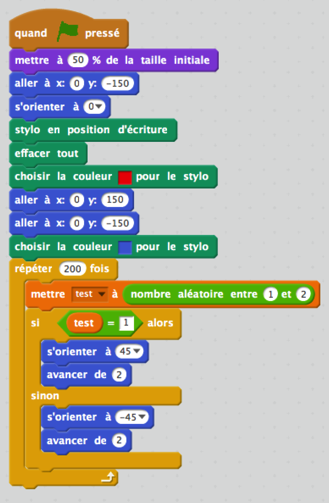
Jeu 2 : « le pari »
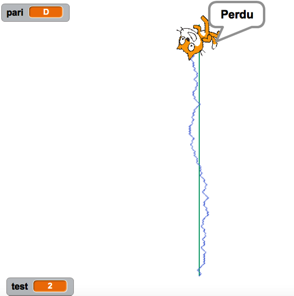
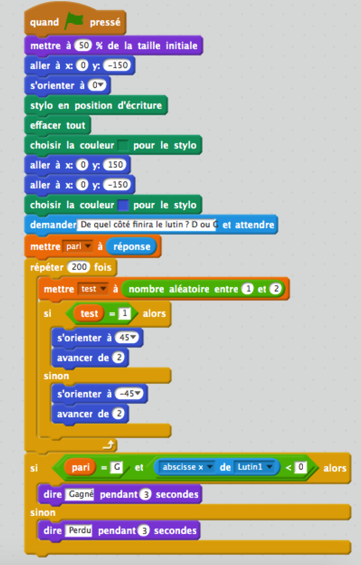
Deuxième marche aléatoire : dans les quatre directions…
Pour conclure cette séance sur les déplacements aléatoires, je propose aux élèves de programmer, en autonomie (et de m’envoyer via e-lyco leur programme), une marche aléatoire du lutin dans les quatre direction.
C’est à dire, en partant du milieu de l’écran, faire déplacement aléatoirement soit vers la droite (orientation à 90°), soit vers la haut (orientation à 0°), soit vers la gauche (orientation à -45°), soit vers le bas (orientation à -90°).
Voici deux exemples de programmes reçus :
Programme 1 :
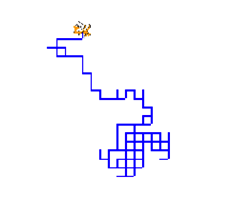
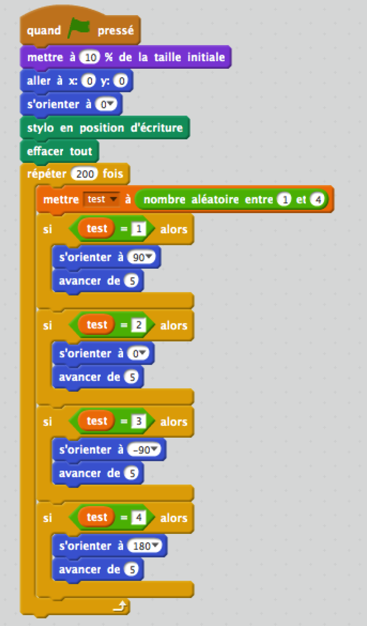
Programme 2 :
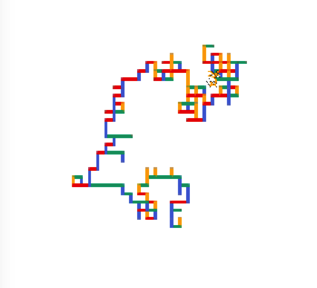
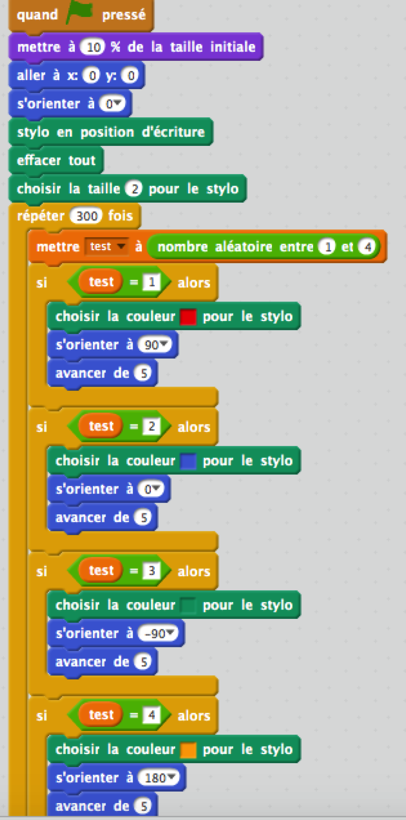
Conclusion
Je suis toujours assez surpris (positivement) de la capacité des élèves à produire des programmes variés (plus ou moins rapidement) sur Scratch, source d’une véritable différenciation pédagogique.
Les élèves ont pris un réel plaisir à programmer ces déplacements et ils ont pris des initiatives intéressantes pour améliorer leurs programmes (couleurs, interactions avec l’utilisateur…).
J’ai trouvé qu’en une heure de travail, le contenu de production fourni par élèves était très positif et que le nombre d’élèves qui ont souhaité poursuivre leurs programmations hors du temps de classe était supérieur à certaines de mes activités habituelles.
Il me semble donc qu’il y a là un levier à exploiter pour les emmener différemment vers les notions mathématiques que nous souhaitons étudier avec eux.
Pour le thème étudiée ici :
Cette approche des phénomènes aléatoires me semble avoir a été intéressante et positive pour plusieurs raisons :
- d’abord parce qu’elle résulte d’une programmation par les élèves eux – mêmes ;
- ensuite parce que la possibilité offerte par Scratch de jouer et rejouer de multiples fois la démarche du lutin permet de bien percevoir que les résultats produits par les programmes dans le cadre de ces déplacements liés au hasard sont très nombreux.
« Il y a une infinité de trajets » a lancé un élève….
Une infinité ?
Vraiment ?
Une porte ouverte vers un dénombrement sympathique…
Stéphane Percot, Enseignant au collège Haxo à La Roche sur Yon (85)
information(s) pédagogique(s)
niveau : tous niveaux, Collèges tous niveaux, 4ème, 3ème
type pédagogique :
public visé : non précisé, élève, enseignant
contexte d'usage : salle multimedia
référence aux programmes :
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA

