espace pédagogique > disciplines du second degré > enseignements informatiques > enseignement > snt
Modéliser les Réseaux Sociaux
mis à jour le 10/06/2020
mots clés : snt, réseaux sociaux, graphes
Résumé : Activités sur papier pour nommer les notions clés autour des graphes et identifier leur traduction dans le cadre des réseaux sociaux. Quelques algorithmes en Python sont inclus et peuvent être présentés par l’enseignant en classes
Point du programme traité
- Contenus : Rayon, diamètre et centre d’un graphe et Notion de « petit monde » Expérience de Milgram
- Capacités attendues : Déterminer ces caractéristiques sur des graphes simples et Décrire comment l’information présentée par les réseaux sociaux est conditionnée par le choix préalable de ses amis.
Lieu de l’activité : En salle simple avec vidéoprojecteur
Matériels / logiciels utilisés : Feuille et crayon / utilisation possible de Python
Durée de l’activité : de 1h30 à 2h00
1) Un réseau du type " Facebook "
Un réseau social est avant tout constituer de personnes qui désirent partager des choses entre elles (médias, information, avis, …) et donc se lier les unes aux autres. Pour comprendre comment se propage les informations, on a cherché un moyen de représenter visuellement l'organisation du réseau social. Et de là est arrivé l'utilisation des graphes
Dans un réseau du genre de " Facebook ", être ami avec quelqu'un nécessite que les deux personnes soient d'accord. On est donc ami de manière symétrique. On va donc représenter chaque personne par une bulle (les sommets du graphe) et chaque relation par un lien entre deux bulles (les arêtes du graphes).
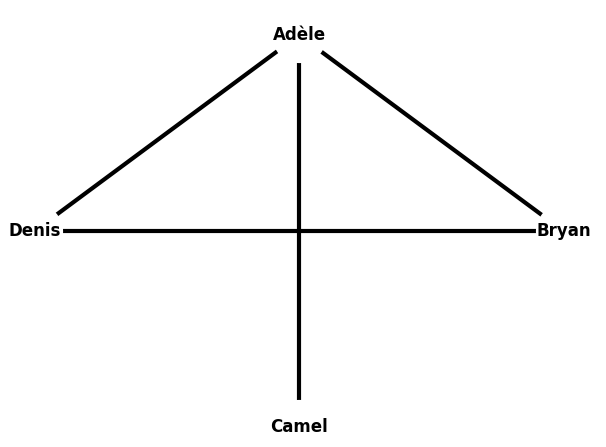 Par exemples, prenons le graphe ci-contre :
Par exemples, prenons le graphe ci-contre :
A faire soi-même :
Construire le graphe de relations amicales du petit groupe suivant :
Corrections : 3 visualisations de la même situation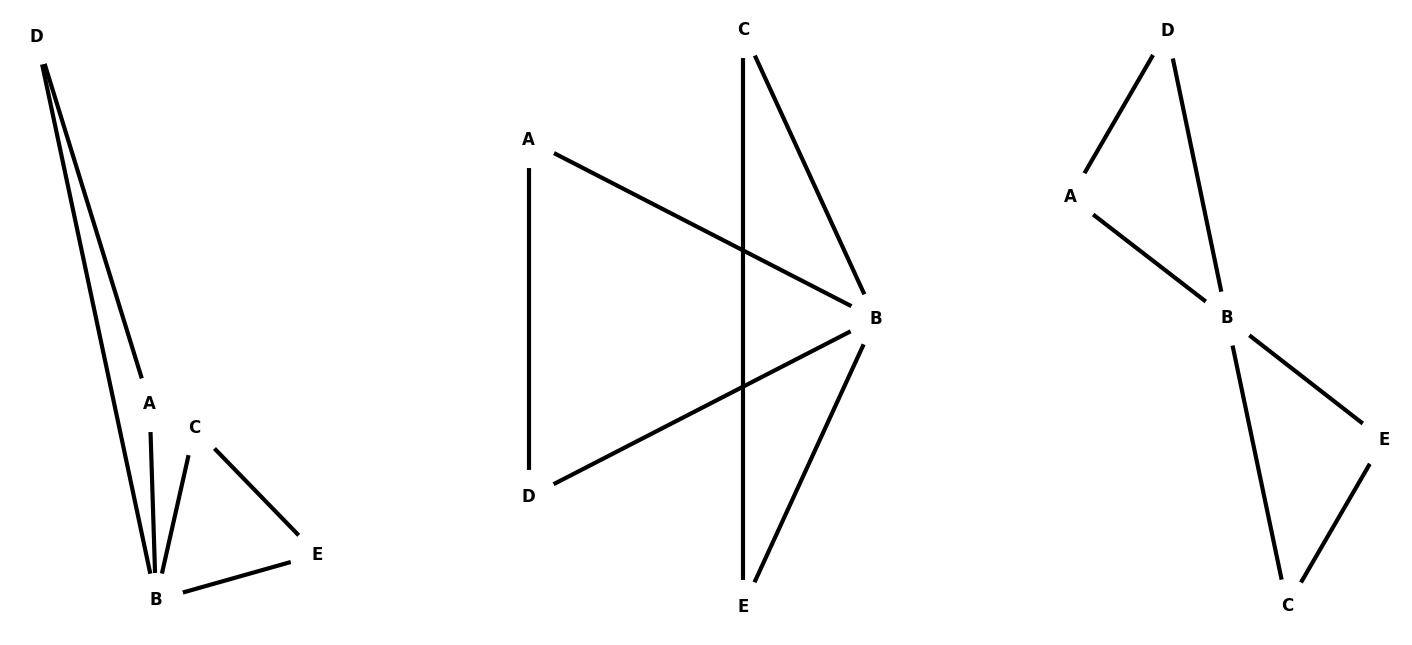
On peut voir apparaitre des informations pertinentes lorsque le graphe est correctement organisé. Dans l'exemple précédent, on voit bien que Benoit est l'élément central du groupe dans la troisième version présentée.
Sur un graphe avec peu de sommets, on peut tester différentes configurations, mais dans la réalité les graphes possèdent des millions de sommets. Il faut donc manipuler des graphes à travers des concepts clairs et des algorithmes.
Dans un réseau du genre de " Facebook ", être ami avec quelqu'un nécessite que les deux personnes soient d'accord. On est donc ami de manière symétrique. On va donc représenter chaque personne par une bulle (les sommets du graphe) et chaque relation par un lien entre deux bulles (les arêtes du graphes).
 Par exemples, prenons le graphe ci-contre :
Par exemples, prenons le graphe ci-contre :- Quels sont les amis de Bryan ?
……………………………………………….. - Denis et Camel sont-ils amis ?
…………. - Combien de sommets le graphe contient-il ? ……………………….
- Combien d'arête contient-il ? ……………………
A faire soi-même :
Construire le graphe de relations amicales du petit groupe suivant :
- Ashley est amie avec Benoit, Dido et Ela
- Benoit est ami avec tout le monde
- Cédric est ami avec Benoit et Ela
- Dido est ami avec Ashley et Benoit
- Ela est amie avec Ashley, Benoit et Cédric
Corrections : 3 visualisations de la même situation

On peut voir apparaitre des informations pertinentes lorsque le graphe est correctement organisé. Dans l'exemple précédent, on voit bien que Benoit est l'élément central du groupe dans la troisième version présentée.
Sur un graphe avec peu de sommets, on peut tester différentes configurations, mais dans la réalité les graphes possèdent des millions de sommets. Il faut donc manipuler des graphes à travers des concepts clairs et des algorithmes.
| Concepts | Définitions | Dans les réseaux sociaux |
|---|---|---|
| Sommet | Point du graphe | Personne inscrite |
| Arête | Lien dans le graphe | Relation entre deux personnes |
| Degrés | Nombre de sommets connectés à un sommet donné | Nombre d' "amis" |
| Distance entre deux sommets | Nombre minimal d'arêtes pour relier deux sommets | Nombre de contact séparant deux personnes |
| Excentricité d'un sommet | Distance maximale entre un sommet et l'ensemble des autres sommets du graphe | Nombre de contacts séparant une personne du reste du réseau |
| Rayon d'un graphe | Valeur minimale de l'excentricité | Identifie les personnes influentes dans le réseau |
| Centre(s) d'un graphe | Sommet(s) ayant l'excentricité minimal | |
| Diamètre d'un graphe | Distance maximale entre deux sommets d'un graphe | Degré de séparation dans le réseau (voir l'expérience de Milgram) |
Etudier chacun des ces concepts dans le graphe suivant :
| 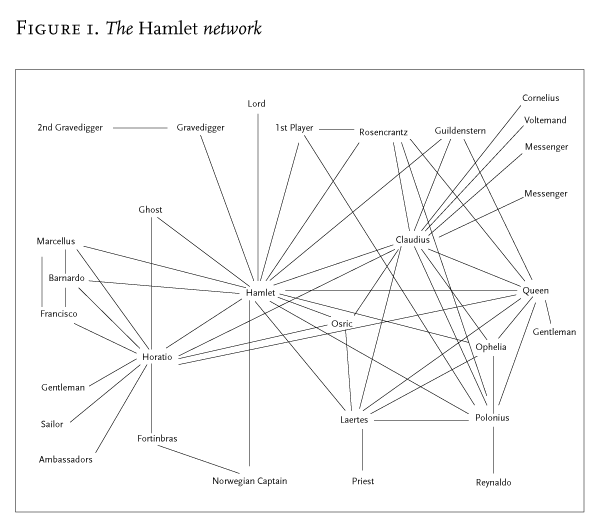 Source : Franco Moretti |
2) Ou de type « Twitter »
Dans un réseau social comme « Twitter », il s’agit de s’abonner à quelqu’un pour suivre ses publications. La relation est à sens unique, si vous suivez quelqu’un cette personne ne vous suit pas forcement.
La représentation de ce type de situation est toujours un graphe mais ses arêtes sont des flèches pour symboliser le sens de la relation : celui qui crée le contenu au début de la flèche, celui qui le récupère à la pointe.
Par exemple :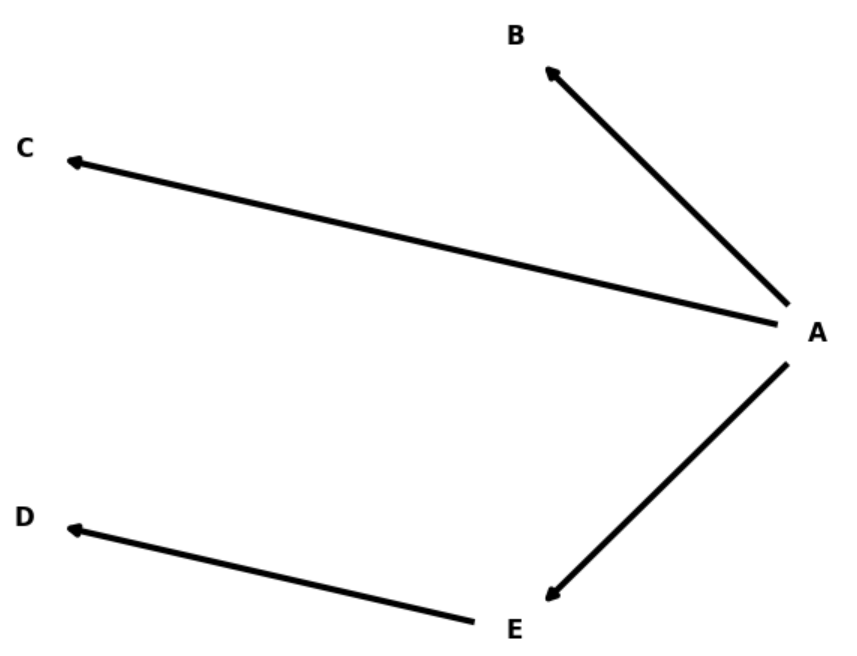
On peut alors définir les mêmes notions qu’avant, attention cependant les relations ne sont plus symétriques. Dans le graphe précédent, les médias publiés par D ne seront pas visibles par B.
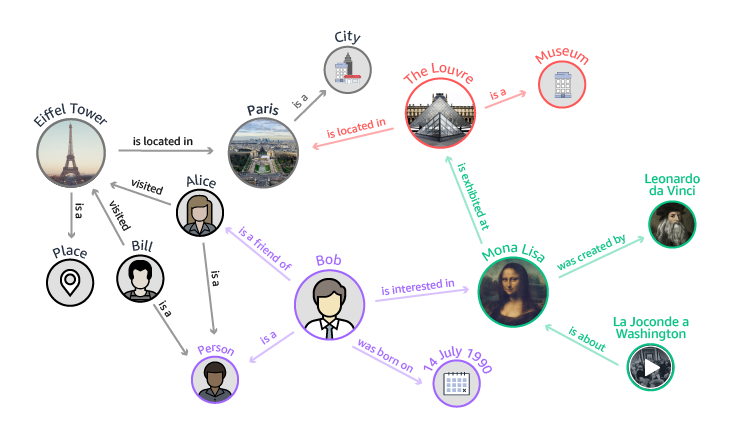
De tels graphes permettent ainsi aux sites de réseaux sociaux de vous proposer de nouveaux contacts en fonction de vos envies et de vos connaissances.
D’après le diagramme précédent, quelle visite pourrait-on conseiller à Bob ?
La représentation de ce type de situation est toujours un graphe mais ses arêtes sont des flèches pour symboliser le sens de la relation : celui qui crée le contenu au début de la flèche, celui qui le récupère à la pointe.
Par exemple :

On peut alors définir les mêmes notions qu’avant, attention cependant les relations ne sont plus symétriques. Dans le graphe précédent, les médias publiés par D ne seront pas visibles par B.

Source : Amazone Neptune
De tels graphes permettent ainsi aux sites de réseaux sociaux de vous proposer de nouveaux contacts en fonction de vos envies et de vos connaissances.
D’après le diagramme précédent, quelle visite pourrait-on conseiller à Bob ?
3) Analyse graphique d’un réseau
a. Les communautés
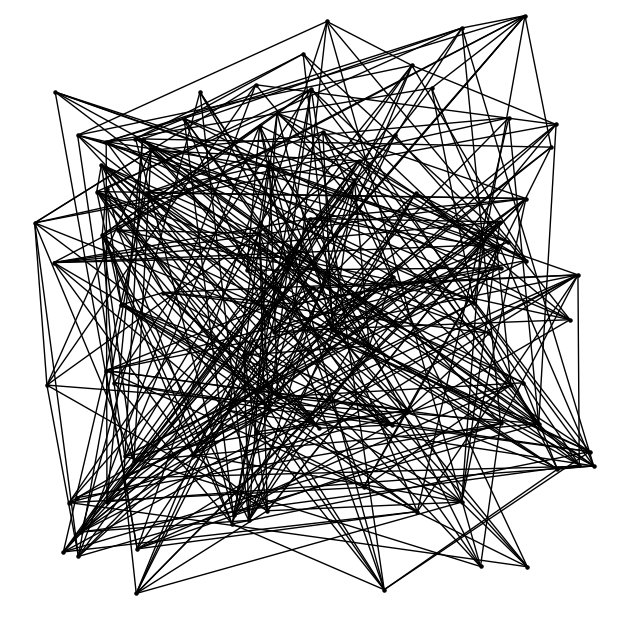 Une fois le réseau modélisé, il est intéressant de l’analyser. Le plus simple est de regarder sa forme graphique même si l’utilisation d’algorithme reste la seule solution lorsque le nombre de sommets devient trop important.
Une fois le réseau modélisé, il est intéressant de l’analyser. Le plus simple est de regarder sa forme graphique même si l’utilisation d’algorithme reste la seule solution lorsque le nombre de sommets devient trop important.
Voici ci-contre, un réseau de 100 personnes avec leurs liens.
Ci-dessous nous les avons arrangés de manière différente.
Cet effet est nommé « clustering », en effet les utilisateurs des réseaux se regroupe autour de quelques points communs et forment des bulles avec peu de liens avec les autres bulles.
b) Les influenceurs
Un autre effet peut aussi être visible une fois le graphe réorganisé. Voici le même réseau sous deux formes différentes :
Que peut-on observer dans cet exemple : …………………………………………………………………………………
……………………………………………………………………………………………………………………………………………
C’est le principe des influenceurs qui peuvent toucher plus de monde, plus rapidement.
 Une fois le réseau modélisé, il est intéressant de l’analyser. Le plus simple est de regarder sa forme graphique même si l’utilisation d’algorithme reste la seule solution lorsque le nombre de sommets devient trop important.
Une fois le réseau modélisé, il est intéressant de l’analyser. Le plus simple est de regarder sa forme graphique même si l’utilisation d’algorithme reste la seule solution lorsque le nombre de sommets devient trop important.Voici ci-contre, un réseau de 100 personnes avec leurs liens.
Ci-dessous nous les avons arrangés de manière différente.
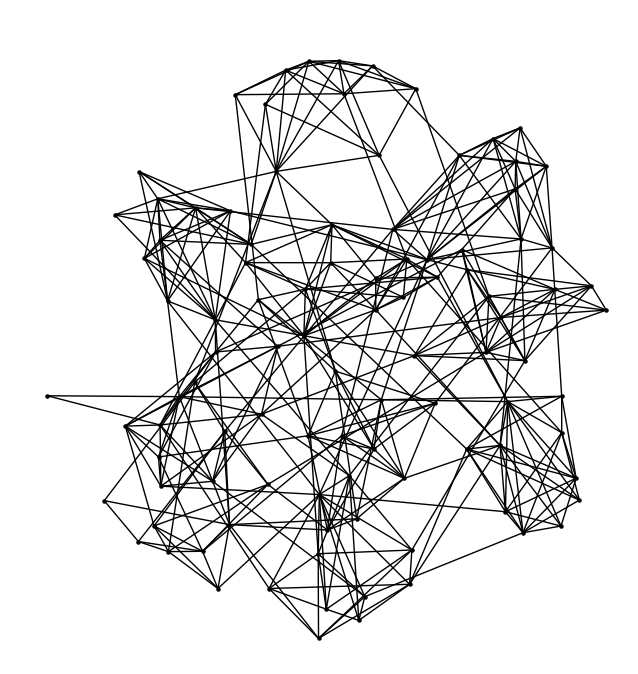 | Que fait apparaitre cette organisation des sommets ? ……………………………………………………………………………………… Quelle peut être la conséquence de cela sur les réseaux sociaux ? ……………………………………………………………………………………… |
Cet effet est nommé « clustering », en effet les utilisateurs des réseaux se regroupe autour de quelques points communs et forment des bulles avec peu de liens avec les autres bulles.
b) Les influenceurs
Un autre effet peut aussi être visible une fois le graphe réorganisé. Voici le même réseau sous deux formes différentes :
| 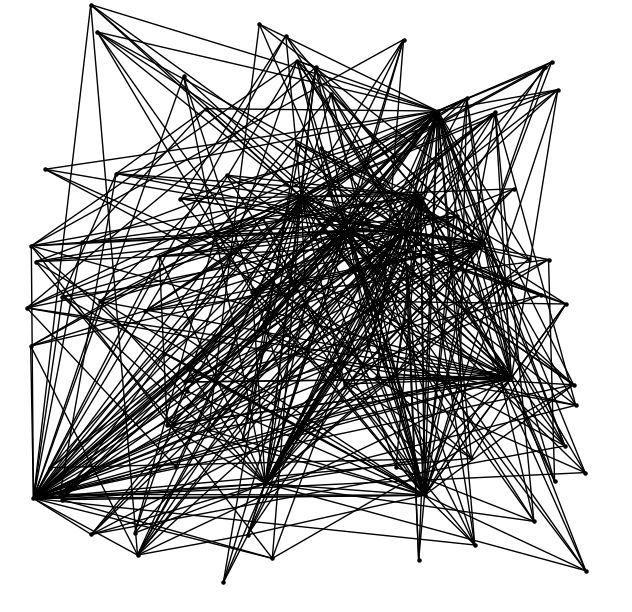 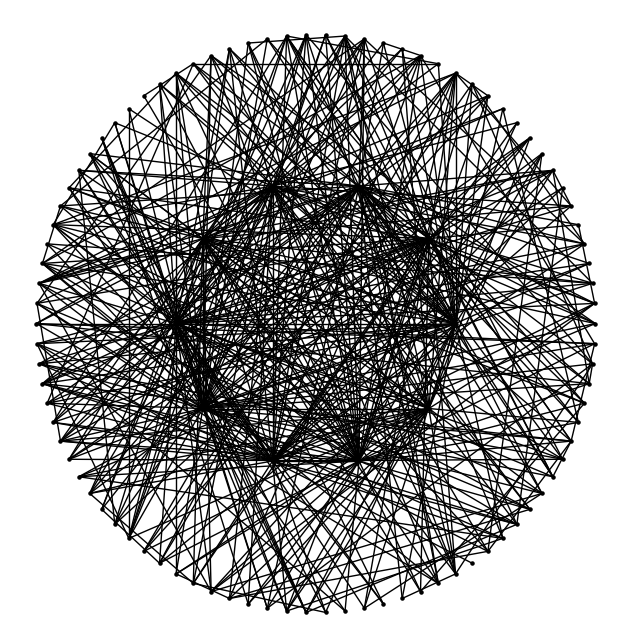 |
……………………………………………………………………………………………………………………………………………
C’est le principe des influenceurs qui peuvent toucher plus de monde, plus rapidement.
Hervé Diet, enseignant au lycée Touchard-Washington (72)
information(s) pédagogique(s)
niveau : tous niveaux, 2nde
type pédagogique : démarche pédagogique
public visé : non précisé, élève, enseignant
contexte d'usage : classe
référence aux programmes :
documents complémentaires
enseignements informatiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA



