mathématiques
s'identifier
portail personnel ETNA
espace pédagogique > disciplines du second degré > mathématiques > mutualisation > vos activités
Recherche d'un lieu géométrique avec barycentre
mis à jour le 09/09/2008
A partir d'une figure réalisée sur un logiciel de géométrie dynamique, caractériser un lieu lorsqu'un point évolue sur un cercle.
mots clés : lieu, justifier, caractériser, barycentre, symétrie
Fiche élève
Enoncé
Dans le plan P, on donne quatre points O, A, B et C et un cercle (
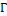) de centre O.Le point M est un point quelconque variable sur le cercle (
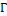). On associe au point M l'unique point M du plan P défini par l'égalité : 
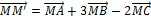.Il s'agit de déterminer le lieu géométrique L du point M lorsque le lieu géométrique du point M est le cercle (
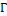).1. A l'aide d'un logiciel de géométrie plane :
(a) construire les points O, A, B et C, le cercle () et un point libre M sur ce cercle.
(b) construire le point M associé à M.
) et un point libre M sur ce cercle.(b) construire le point M associé à M.
Appeler l'examinateur pour une vérification de la construction faite.
(c) En observant plusieurs positions du point M faire une conjecture sur la nature de la transformation du plan qui transforme M en M ainsi que la nature du lieu géométrique du point M.
Appeler l'examinateur pour une vérification de la figure réalisée et de la conjecture faite.
2.
(a) Déterminer la nature de la transformation du plan qui transforme le point M en le point M.
(b) Déterminer le lieu géométrique L du point M.
Production demandée
- La figure réalisée avec le logiciel de géométrie dynamique.
- La justification de la nature de la transformation.
- La caractérisation du lieu géométrique de M et sa justification.
- La justification de la nature de la transformation.
- La caractérisation du lieu géométrique de M et sa justification.
Correction
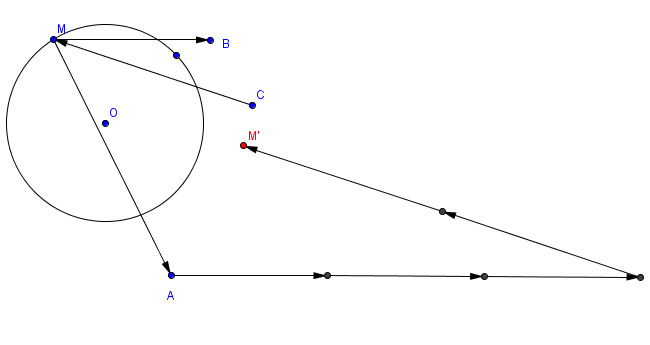
Corrigé du 1)
Vérifier que le point M est bien lié au point M.
Difficulté pour les élèves : construire la somme de vecteurs avec geogebra.
Corrigé du 2) :
a) Soit G barycentre de (A,1), (B,3) et (C,2), 1+32=20
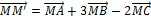équivaut à 
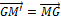donc G est le milieu de [MM]La transformation du plan qui transforme le point M en M est la symétrie centrale de centre G.
b) L'image d'un cercle par une symétrie centrale est un cercle de même rayon
L'image du cercle par la symétrie de centre G est le cercle de même rayon et dont le centre est l'image de O.
L'exercice pourra être redemandé avec d'autres coefficients pour une homothétie de centre G et rapport ...
information(s) pédagogique(s)
niveau : 1ère S
type pédagogique : non précisé
public visé : enseignant, élève
contexte d'usage : non précisé
référence aux programmes :
documents complémentaires
DOC
PDF
geogebramathématiques - Rectorat de l'Académie de Nantes