mathématiques
s'identifier
portail personnel ETNA
espace pédagogique > disciplines du second degré > mathématiques > des maths > olympiades
Exercices d'entraînement
Exercice 1 : les deux nageurs
Deux nageurs ayant l'habitude de nager à la même vitesse font un parcours de même longueur en partant à la même heure mais l'un nage en eau calme pendant que l'autre fait un aller et retour dans une rivière en subissant l'influence du courant (le courant de la rivière est constant).
Lequel arrivera le premier ?
(l'aller est aussi long que le retour et les nageurs ne perdent pas de temps dans les virages).
Lequel arrivera le premier ?
(l'aller est aussi long que le retour et les nageurs ne perdent pas de temps dans les virages).
Exercice 2 : entiers naturels
16 + 17 + 18 + 19 + 20 = 21 + 22 + 23 + 24
Y a-t-il d'autres entiers naturels consécutifs tels que la somme des n + 1 premiers soit égale à la somme des n suivants ?
Et pour la somme des carrés ?
(10² + 11² + 12² = 13² + 14² et 21² + 22² + 23² + 24² = 25² + 26² + 27² sont des solutions, y en a-t-il d'autres ?).
Y a-t-il d'autres entiers naturels consécutifs tels que la somme des n + 1 premiers soit égale à la somme des n suivants ?
Et pour la somme des carrés ?
(10² + 11² + 12² = 13² + 14² et 21² + 22² + 23² + 24² = 25² + 26² + 27² sont des solutions, y en a-t-il d'autres ?).
Exercice 3 : la course de chevaux
Terracher, 1 S Analyse, Hachette 2001.
Les n chevaux d'une course sont numérotés 1 ; 2 ; ....... ; n.
Un des chevaux, blessé ne part pas. La somme des numéros des partants est 260.
Combien y a-t-il eu de partants ? Quel est le numéro du cheval blessé ?
Exercice 4 : point de vue
Terracher, 1 S Analyse, Hachette 2001.
Un mobile M décrit la parabole d'équation y = - x2 + 17x - 66 dans le sens des « x croissants ».Un observateur est placé en P(2 ; 0).
Déterminer les valeurs de l'abscisse de M pour lesquelles M est « visible » depuis P.
Exercice 5 : le plus grand cône
Terracher, 1 S Analyse, Hachette 2001.
Dans un disque de rayon R, on découpe un secteur circulaire de 
radian. En joignant les deux bords droits du secteur restant, on fabrique un cône.
Pour quelle valeur de le volume du cône est-il maximal ?
Exercice 6 : drapeau
Hyperbole 1 S 108 p. 54 (d'après Challenge australien)
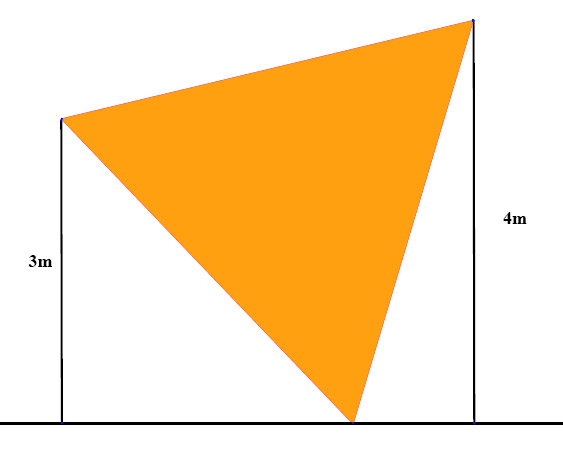
Le drapeau ci-contre a la forme d'un triangle équilatéral.
Il est suspendu par deux de ses coins au sommet de mâts verticaux de 3m et 4m de
haut. Le troisième coin affleure exactement au sol.
Quelle est la longueur du côté de ce drapeau?
Il est suspendu par deux de ses coins au sommet de mâts verticaux de 3m et 4m de
haut. Le troisième coin affleure exactement au sol.
Quelle est la longueur du côté de ce drapeau?
Exercice 7 : un nageur
source : Revue Logimath N° 3(Janvier 2006)
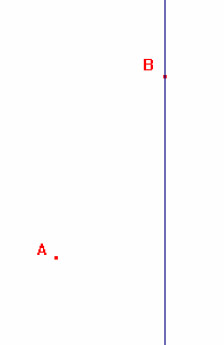
Un nageur se trouve dans l'eau au point A. Il veut rejoindre un point B situé sur le rivage.
Sa vitesse dans l'eau est deux fois moins élevée que sa vitesse sur terre.
En quel point doit-il accoster pour atteindre B le plus vite possible ?
Sa vitesse dans l'eau est deux fois moins élevée que sa vitesse sur terre.
En quel point doit-il accoster pour atteindre B le plus vite possible ?
Exercice 8 : Ecriture décimale illimitée périodique
Rappels :
Un nombre
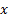est dit décimal lorsqu'il existe 
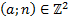tel que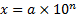 
Un nombre
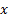est dit rationnel lorsqu'il existe 
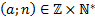tel que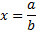 
Un nombre x est dit irrationnel lorsqu'il n'est pas rationnel.
Enoncé
Quand on divise 1 par 11, on obtient 0,090909090909... On dira que cette écriture décimale est l'écriture décimale illimitée de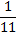 
.
Les chiffres 0 et 9 se succèdent indéfiniment. On dira que cette écriture décimale est périodique et on écrira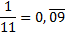
. Ainsi
.
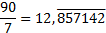On remarquera que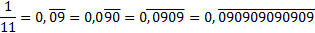
.
On appellera longueur de la période le nombre de chiffres minimum de la période et on désignera dans la suite par période, la plus petite des périodes.
Le but de l'exercice est de prouver qu'un nombre est rationnel si et seulement si il admet une écriture décimale illimitée périodique.
Partie I
a. Déterminer l'écriture décimale illimitée périodique de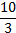
; 
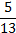puis de 
.
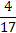b. Quelle est la longueur maximale de la période de l'écriture décimale de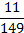
?
c. Justifier que tout nombre rationnel est ou un nombre décimal ou admet une écriture décimale illimitée périodique.
d. A quel nombre correspond l'écriture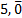
? A quoi est égal 
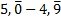? Que peut-on en conclure ?
Partie II
Nous venons d'établir que tout nombre rationnel avait au moins une écriture décimale illimitée périodique. On s'intéresse maintenant au problème réciproque. On va tenter de démontrer que toute écriture décimale illimitée périodique est l'écriture d'un nombre rationnel
a. Etude d'un exemple.
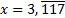. Calculer 
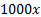puis montrer que 
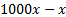est un nombre entier. Déterminer une fraction irréductible égale à .
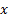b. Appliquer la méthode précédente à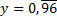
.
c. Déterminer une fraction irréductible égale à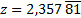
.
d. Justifier que si un nombre admet une écriture décimale illimitée périodique, alors ce nombre est rationnel. Conclure.
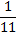.Les chiffres 0 et 9 se succèdent indéfiniment. On dira que cette écriture décimale est périodique et on écrira
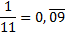. Ainsi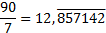.On remarquera que
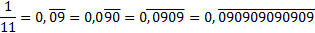.On appellera longueur de la période le nombre de chiffres minimum de la période et on désignera dans la suite par période, la plus petite des périodes.
Le but de l'exercice est de prouver qu'un nombre est rationnel si et seulement si il admet une écriture décimale illimitée périodique.
Partie I
a. Déterminer l'écriture décimale illimitée périodique de
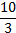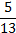; puis de 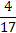.b. Quelle est la longueur maximale de la période de l'écriture décimale de
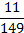?c. Justifier que tout nombre rationnel est ou un nombre décimal ou admet une écriture décimale illimitée périodique.
d. A quel nombre correspond l'écriture
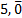? A quoi est égal 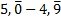? Que peut-on en conclure ?Partie II
Nous venons d'établir que tout nombre rationnel avait au moins une écriture décimale illimitée périodique. On s'intéresse maintenant au problème réciproque. On va tenter de démontrer que toute écriture décimale illimitée périodique est l'écriture d'un nombre rationnel
a. Etude d'un exemple.
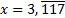. Calculer 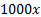puis montrer que 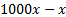est un nombre entier. Déterminer une fraction irréductible égale à 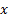.b. Appliquer la méthode précédente à
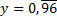.c. Déterminer une fraction irréductible égale à
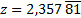.d. Justifier que si un nombre admet une écriture décimale illimitée périodique, alors ce nombre est rationnel. Conclure.
mathématiques - Rectorat de l'Académie de Nantes