espace pédagogique > disciplines du second degré > mathématiques > enseignement > activités pédagogiques
caméléon et araignée
mis à jour le 06/01/2014
Cette activité revisite le problème de distance minimale entre deux objets. Un caméléon souhaite attraper une araignée avec sa langue et doit se rapprocher suffisamment pour cela.
mots clés : distance, calculatrice, algorithmique, Halloween
Les objectifs
- Utiliser le travail effectué sur les distances dans un repère orthonormé.
- Réactiver la notion de fonction vue au collège.
- Utiliser un algorithme pour automatiser le calcul.
- Première utilisation de la calculatrice.
Eléments de mise en œuvre
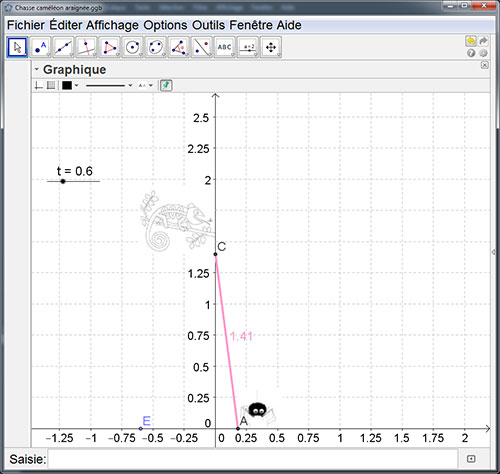
Les élèves étaient placés en groupe de 3 (10 groupes en tout). Ils ont eu une demi-heure de recherche.
L'heure suivante a été consacrée à la mise en commun et à la recherche de solutions.
Comment faire pour obtenir tous les cas ? A cette occasion a été présentée l'animation Geogebra.
Deux heures en 1/2 classe, avec ordinateurs et calculatrices, ont ensuite été nécessaires pour traiter la construction point par point de la courbe (Partie A) et l'utilisation de l'algorithme (Partie B) et enfin utiliser cette fonction pour une première approche de la calculatrice.
Informations complémentaires sur la mise en œuvre :
- En groupe : assez rapidement, les élèves ont eu l'idée de faire un dessin. Ils prouvent qu'au bout de deux secondes le caméléon peut attraper l'araignée. Le problème est : peut-il le faire avant ? Les élèves commencent à traiter le cas de 0s et de 1s. Beaucoup de groupe ont du mal à envisager d'autres cas...Ils éprouvent aussi des difficultés à s'organiser correctement pour traiter plusieurs cas en même temps, chaque élève ne faisant pas le même calcul. (repris dans le bilan effectué ensuite en classe entière).
- En classe entière : les élèves acceptent, en voyant les différents bilans que d'autres cas peuvent et doivent être envisagés. Je leur propose alors l'animation sous geogebra avec un pas de 0,1. Les élèves visualisent que le caméléon peut attraper l'araignée avant les deux secondes. La modélisation par l'intermédiaire d'une lettre n'est cependant pas donnée spontanément. Je leur souffle que l'on peut envisager une variable. Ils trouvent difficilement les coordonnées du caméléon et de l'araignée, pensent aux calculs de distance mais les lettres leur posent un gros problème et je décide de ne pas insister (ce cas de calcul de distance sera revu en questions rapides un peu plus tard...et dans la séance en demi groupe)
- En 1/2 groupe. Je leur propose la construction point par point de la courbe d'une fonction relativement difficile (en fait la distance entre les deux animaux - cette remarque viendra au cours de la séance par certains élèves qui s'étonnent de la présence de la racine carrée et font le lien avec le problème traité dans la semaine...). Les calculs d'images et les premiers placements de points sont difficiles pour beaucoup d'élèves ( là, je suis surpris - ce calcul a déjà été fait par la plupart des élèves - beaucoup d'élèves m'ont fait part en début d'année de leurs difficultés en maths - option Littérature et société?). En allant les voir un à un, je leur demande comment peut-on automatiser les calculs ? La plupart voit alors l'intérêt d'utiliser un algorithme ( outil introduit quelques semaines auparavant lors des séances de 1/2 groupe).
- Un algorithme possible est alors donné au rythme des demandes - pour certains ils ont calculé une dizaine d'images avant d'y penser. ( A mon sens, il est encore trop tôt pour leur demander de le construire entièrement). Les élèves doivent le lire, le comprendre puis aller le modifier sous algobox pour augmenter le nombre de points de la courbe.
- Je reste sur cette fonction pour introduire l'utilisation de la calculatrice : rentrer une fonction - visualiser la table - visualiser la courbe dans une fenêtre donnée (avec un travail sur les parenthèses et sur les signes « - » de la machine). L'outil calculatrice devient alors un outil qu'ils doivent avoir avec eux pour conjecturer les propriétés des fonctions (dans la semaine suivante, chaque fonction étudiée sera injectée dans la calculatrice pour proposer différentes conjectures...). Ce travail est effectué en autonomie par groupe de 2 en s'appuyant sur la fiche adaptée du site IREM de Lyon : « 36 élèves , 36 calculatrices ». D'autres fonctions sont ensuite proposées au fur et à mesure que les élèves terminent la fiche.
Bilan
Cela a permis au professeur de voir où ils en étaient sur la notions de fonctions, de se rendre compte de la difficulté d'introduire une variable (les problèmes suivants en tiendront compte), de continuer à travailler les calculs d'images simples « à la main » et par l'intermédiaire d'une machine....
Fabriche Foucher, enseignant au lycée lycée Jacques Prévert à Savenay (44)
information(s) pédagogique(s)
niveau : tous niveaux, Lycée tous niveaux, 2nde
type pédagogique :
public visé : enseignant, élève
contexte d'usage : classe
référence aux programmes :
documents complémentaires
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA



