espace pédagogique > disciplines du second degré > mathématiques > enseignement > activités pédagogiques
Equations différentielles et tableur
mis à jour le 26/09/2007
mots clés : équation différentielle, tableur
Considérons l'équation différentielle y ' = 0,4y
Cherchons une éventuelle solution vérifiant la condition initiale f(0) = 5
La fonction f est une solution de l'équation posée donc f ' (0) = 0,4 f(0) .
On peut déduire f ' (0) = 2.
Or f ' (0) est peu différent de (f (0 + h ) - f (0)) / h pour h "petit" (non nul)
Il suffit dont de choisir h "petit" ce qui permet d'obtenir une valeur approchée de f ( h ) qui est f (0) + h f ' (0)
Je choisis par exemple h = 0,1 et je trouve f (0,1) peu différent de 5,2
La fonction f est une solution de l'équation posée donc f ' (0,1) = 0,4 f(0,1) .
On peut déduire f ' (0,1) peu différent de 2,08
et ainsi de suite.
On calcule successivement f(0,2) puis f ' (0,2) puis f(0,3) puis f ' (0,3) etc...
Les valeurs obtenues figurent dans le tableau ci-dessous.
Ce principe est généralisable à n'importe quelle équation différentielle et permet donc d'explorer des situations variées. Cette approche permet de "comprendre expérimentalement" l'existence et l'unicité de solution vérifiant une condition initiale donnée. (dans le cas de l'exemple la condition initiale est la donnée d'une valeur de la fonction en un point).
Dans le cas des équations diférentielles qui font l'objet d'une étude théorique dans le cadre du programme, on peut comparer avec intérêt le résultat théorique et le résultat "expérimental". Le choix de h= 0,1 dans le cas de l'exemple parait alors trop grand.
Le tableur va permettre de choisir h ( le pas). Dans le cas de l'exemple précédent,on peut par exemple rapidement calculer f(1) à partir de f(0) avec 10000 séries de calculs ( f '(0) , f(0,0001) puis f ' (0,0001) puis f(0,0002) puis f ' (0,0002) etc...
Le tableur va permettre également de tracer la courbe représentative de la fonction trouvée ce qui permet de "voir" la fonction, de comprendre que l'existence et l'unicité de solution correspond à l'existence et à l'unicité de courbe passant par un point donné (pour le cas de l'exemple précédent). Cette visualisation de courbe représentative de fonction définie sur un intervalle donné permettra plus tard d'y voir plus clair dans les problèmes de "raccordement" fréquemment rencontrés avec les équations différentielles.
Valeurs obtenues avec l'exemple traité:
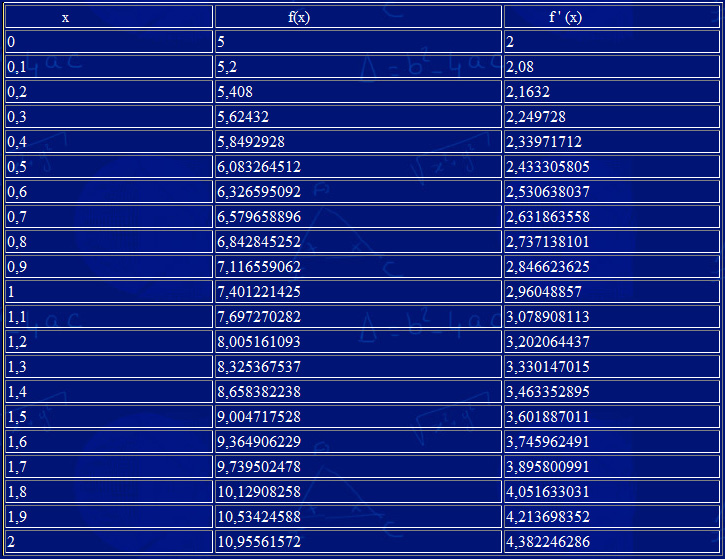
Le même principe peut être retenu pour l'étude des mouvements de corps célestes et en particulier pour le problème des deux corps
Cherchons une éventuelle solution vérifiant la condition initiale f(0) = 5
La fonction f est une solution de l'équation posée donc f ' (0) = 0,4 f(0) .
On peut déduire f ' (0) = 2.
Or f ' (0) est peu différent de (f (0 + h ) - f (0)) / h pour h "petit" (non nul)
Il suffit dont de choisir h "petit" ce qui permet d'obtenir une valeur approchée de f ( h ) qui est f (0) + h f ' (0)
Je choisis par exemple h = 0,1 et je trouve f (0,1) peu différent de 5,2
La fonction f est une solution de l'équation posée donc f ' (0,1) = 0,4 f(0,1) .
On peut déduire f ' (0,1) peu différent de 2,08
et ainsi de suite.
On calcule successivement f(0,2) puis f ' (0,2) puis f(0,3) puis f ' (0,3) etc...
Les valeurs obtenues figurent dans le tableau ci-dessous.
Ce principe est généralisable à n'importe quelle équation différentielle et permet donc d'explorer des situations variées. Cette approche permet de "comprendre expérimentalement" l'existence et l'unicité de solution vérifiant une condition initiale donnée. (dans le cas de l'exemple la condition initiale est la donnée d'une valeur de la fonction en un point).
Dans le cas des équations diférentielles qui font l'objet d'une étude théorique dans le cadre du programme, on peut comparer avec intérêt le résultat théorique et le résultat "expérimental". Le choix de h= 0,1 dans le cas de l'exemple parait alors trop grand.
Le tableur va permettre de choisir h ( le pas). Dans le cas de l'exemple précédent,on peut par exemple rapidement calculer f(1) à partir de f(0) avec 10000 séries de calculs ( f '(0) , f(0,0001) puis f ' (0,0001) puis f(0,0002) puis f ' (0,0002) etc...
Le tableur va permettre également de tracer la courbe représentative de la fonction trouvée ce qui permet de "voir" la fonction, de comprendre que l'existence et l'unicité de solution correspond à l'existence et à l'unicité de courbe passant par un point donné (pour le cas de l'exemple précédent). Cette visualisation de courbe représentative de fonction définie sur un intervalle donné permettra plus tard d'y voir plus clair dans les problèmes de "raccordement" fréquemment rencontrés avec les équations différentielles.
Valeurs obtenues avec l'exemple traité:

Le même principe peut être retenu pour l'étude des mouvements de corps célestes et en particulier pour le problème des deux corps
Youri Gautier
information(s) pédagogique(s)
niveau : Terminale S
type pédagogique : exercice
public visé : enseignant, élève
contexte d'usage : non précisé
référence aux programmes :
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA
