espace pédagogique > disciplines du second degré > mathématiques > enseignement > activités pédagogiques
matrice associée à une transformation du plan et sa réciproque
mis à jour le 19/06/2017
Plusieurs motivations : correspondance équation matricielle et système d'équations linéaires ; produit matriciel comme une action géométrique ; interprétation matricielle d'un problème géométrique pour donner du sens à l'inversion d'une matrice.
mots clés : matrice, transformation, spé maths, enseignement spécifique
- travailler la correspondance équation matricielle et système d'équations linéaires (question 5) ;
- penser le produit matriciel comme une action géométrique (ensemble de l'activité) ;
- utiliser l'interprétation matricielle d'un problème géométrique pour donner du sens à l'inversion d'une matrice (questions 6bc).
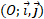
On considère la transformation géométrique du plan qui à tout point M de coordonnées
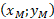 associe le point N de coordonnées :
associe le point N de coordonnées : 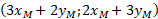 .
.2. Recopier le programme en Python ci-contre .
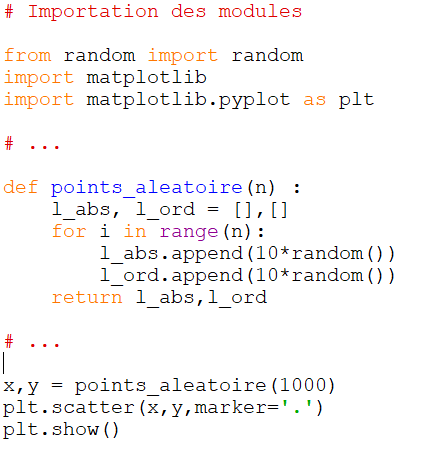
Que permet-il de faire ? (Vous pouvez compléter les commentaires)
3. On souhaite maintenant observer l'image d'un carré par cette application.
Modifier le programme ci-contre pour qu'il choisisse au hasard 10000 fois un point dans un carré de côté 10 unités, et affiche son point image par cette application.
Que constate-t-on ?
Peut-on obtenir n'importe quel point du plan par cette application ?
4. A l'aide d'un système d'équations linéaires, montrer qu'il existe un unique point M dont l'image par cette application est N(4 ; 5). Donner ses coordonnées.
Remarque : D'une façon générale, pour un point quelconque N
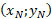 du plan, on peut montrer qu'il existe un unique point M dont l'image par cette application est N. Les coordonnées du point M sont alors données par les formules :
du plan, on peut montrer qu'il existe un unique point M dont l'image par cette application est N. Les coordonnées du point M sont alors données par les formules :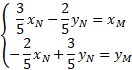
5. Déterminer la matrice A telle que le système d'équations
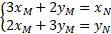 soit équivalent à l'égalité :
soit équivalent à l'égalité : 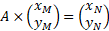
De même, déterminer la matrice B telle que le système
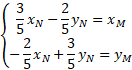 soit équivalent à l'égalité :
soit équivalent à l'égalité : 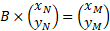
6.
| Casio | TI | Numworks |
| - accéder au menu RUN-MAT - appuyer sur F3 (>MAT) - sélectionner une matrice (Mat A, Mat B, …) et entrer ses dimensions, puis ses coefficients. La matrice est mémorisée ; lors des calculs, appeler la matrice A par SHIFT 2 ALPHA A | - appuyer sur la touche Matrice - grâce à la flèche droite, accéder au menu EDIT - sélectionner une matrice ([A], [B], …) et entrer ses coefficients. La matrice est mémorisée ; lors des calculs, appeler la matrice A par la touche Matrice et choisir [A] | - Appuyer sur la touche "Boîte à outils" - Sélectionner le menu "Matrice" - Sélectionner le premier choix obtenu [[1, 2] [3,4]] |
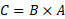
c. Calculer alors la produit matriciel
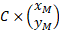
Le résultat obtenu est-il normal compte tenu de ce qu'il représente géométriquement ?
Des éléments de réponses à lire dans la fiche associée, en téléchargement ci-dessous.
les petites fabriques du Maine et Loire
information(s) pédagogique(s)
niveau : tous niveaux
type pédagogique :
public visé : non précisé
contexte d'usage :
référence aux programmes :
documents complémentaires
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA


