espace pédagogique > disciplines du second degré > mathématiques > enseignement > activités pédagogiques
modélisation des quatre opérations à l'aide du schéma en barre - saison 1
mis à jour le 06/07/2023
Une expérimentation sur la mobilisation des opérations à l'aide des schémas en barres, en résolution de problèmes, dans 4 classes de sixième.
mots clés : automatisme, schéma en barres, opération, représenter, modéliser, labo maths
Mise en oeuvre
Ce document a pour objectif d'expliciter la mise en œuvre de notre expérimentation sur la mobilisation des opérations à l'aide des schémas en barres. Pour plus de détail, on pourra se référer au document « Présentation et analyse ». En effet, l'objectif d'automatisation recherché à travers l'utilisation de ces ressources vient en complément d'un indispensable travail sur le sens des opérations, détaillé dans le deuxième document.
On n’exige jamais le résultat final (mais l’élève peut l’indiquer), seulement l’opération mobilisée.
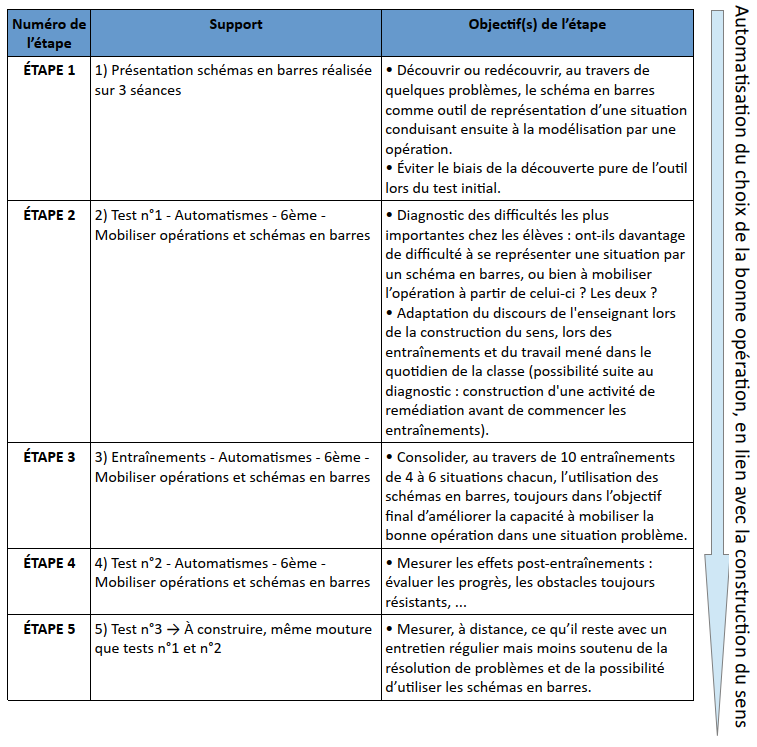
ÉTAPE 1
Nous avons expliqué le principe des schémas en barres (cf document 1 »Présentation Schémas en
barres »).
Certains élèves (peu, moins d’un tiers) connaissent déjà les schémas en barres. Nous nous
appuyons pour cette étape sur 6 problèmes, abordés sur 3 séances successives, en début d’heure à
chaque fois.
- Séance n°1 : les élèves résolvent deux problèmes simples (les opérations à mobiliser sont l’addition et la soustraction), et lors de la correction collective on présente un schéma en barres correspondant au problème.
- Séance n°2 : les élèves résolvent deux problèmes simples (les opérations à mobiliser sont la multiplication et la division), et lors de la correction collective on présente un schéma en barres correspondant au problème.
- Séance n°3 : les élèves ont deux problèmes pour lesquels ils doivent choisir un schéma en barres parmi les trois proposés à chaque fois ; ils doivent ensuite indiquer l’opération correspondante.
ÉTAPE 2
Cette étape a été menée entre les vacances de Noël et les vacances d’hiver.
Nous avons fait passer, en classe, aux élèves de 4 classes de sixième le test n°1 (voir document « Test n°1 -Automatismes - 6ème - Mobiliser opérations et schémas en barres »), qui donne lieu à trois indicateurs de réussite.
- Un premier indicateur pour passer du schéma en barres vers l’opération.
- Un deuxième qui mesure l’aptitude à passer du problème vers le schéma en barres.
- Un dernier du problème vers l’opération, indépendamment de la maîtrise du schéma en barres.
ÉTAPE 3
Cette étape a été menée du mois de janvier au mois d’avril.
Elle consiste en 10 entraînements, construits dans une idée de progressivité de la difficulté et de distinction des objectifs.
- Dans les premiers entraînements on donne la schématisation et on attend l’opération. (l’élève doit donc modéliser avec la bonne opération).
- Dans les entraînements suivants, l’élève doit, à partir d’énoncés de problèmes, choisir la bonne schématisation, et modéliser par la bonne opération.
- Enfin, les élèves doivent produire eux-mêmes la schématisation à partir des énoncés.
Les entraînements sont faits en début de cours, à l’aide d’un livret individuel (cf
document « Entraînements - Automatismes - 6ème - Mobiliser opérations et schémas en barres »).
Les élèves notent leur temps chaque jour (un chronomètre est déclenché au début de l’activité),
puis leur « score » indicatif, rendent le livret qui leur sera re-distribué à la séance suivante.
Après ce temps individuel s’ensuit un temps collectif de correction, qui peut durer une dizaine de minutes en fonction des ambiguïtés à lever, ou des remarques que l’enseignant choisit de faire (cf document Analyse). Très concrètement, nos expérimentations nous ont conduits à élaborer une procédure type que nous avons mobilisée tout au long de ces entraînements.
- Connaît-on le total ou bien est-ce ce que l’on cherche ? (pour les problèmes où le total est connu ; il est explicitement indiqué « en tout » dans certains problèmes, dans d’autres il faut le comprendre avec le contexte).
- Quelle autre information puis-je porter dans le schéma en barres (on peut toujours indiquer deux informations, la troisième est ce que l’on cherche).
- Je place le point d’interrogation sur l’information manquante.
- Quelle opération fais-je pour que son résultat soit la valeur qui se cache derrière le point d’interrogation ?
Cette procédure-type, d’abord portée par l’enseignant.e, devient assez rapidement mobilisable et mobilisée par les élèves.
ÉTAPE 4
Cette étape a été menée entre les vacances d’hiver et les vacances de Pâques, avec comme document support un test n°2, qui avait la même mouture que le test n°1, et que les élèves ont donc passé après les 10 entraînements de l’étape 3. L’idée est de mesurer la progression entre les deux tests et les difficultés persistantes.
ÉTAPE 5
Cette étape sera menée en début de classe de cinquième avec comme document support un test n°3, qui aura la même mouture que les tests n°1 et n°2, « pour voir ce qu’il en reste » lors de la résolution de problèmes.
ÉTAPE TRANSVERSALE AUX AUTRES
Continuer de confronter en dehors de ces temps les élèves à des problèmes, à plusieurs étapes,
plus ou moins complexes, etc.
Exemple
laboratoire de mathématiques, collège Ernest Renan - Saint Herblain (44)
information(s) pédagogique(s)
niveau : tous niveaux
type pédagogique :
public visé : non précisé
contexte d'usage :
référence aux programmes :
ressources associées

|
modélisation des quatre opérations à l'aide du schéma en barre - saison 2 | 06/11/2024 |
| Une expérimentation sur la mobilisation des opérations à l'aide des schémas en barres, en résolution de problèmes, dans 4 classes de sixième. | ||
| automatisme, schéma en barres, opération, représenter, modéliser, labo maths | laboratoire de mathématiques | |
documents complémentaires
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA