mathématiques

espace pédagogique > disciplines du second degré > mathématiques > enseignement > activités pédagogiques

produit scalaire - une ligne de niveau

mis à jour le 06/06/2019

Un exemple de mise en oeuvre de la différenciation utilisant le produit scalaire.

mots clés : produit scalaire, spécialité, ligne niveau, ressource lycée

Il s’agit alors :

De permettre à chaque élève de consolider les acquis du collège.
D’assurer les bases mathématiques nécessaires à toutes les poursuites d’études au lycée.
Les activités rapides qui suivent donnent quelques exemples qui peuvent être proposés tout au long de l’année de seconde, et poursuivis (répétés) en enseignement de spécialité de première afin de prévenir les difficultés dues aux nombreux obstacles que peut augurer cette démonstration.

Les commentaires sont en orange dans le texte.

Dès la classe de seconde

S’appuyer sur des bases de géométrie de collège et les compléter

Combien mesure le diamètre du cercle circonscrit à un rectangle ?
Que peut-on dire des diagonales d’un rectangle ?
Que signifie « A et B sont deux points diamétralement opposés » ?
ABCD est un rectangle.
Le cercle tracé est le cercle circonscrit à ce rectangle.
Caractériser le centre du cercle circonscrit à ce rectangle.

- Ce verbe « caractériser » pourra ne pas être compris par des élèves entrant en seconde, la différenciation, vecteur de compréhension, passera par la reformulation :
Où est situé le point O, centre du cercle circonscrit ?
Quel est le centre du cercle circonscrit, qu’on nommera O ?
- Anticiper en réactivant les prérequis est une base essentielle de la différenciation : le programme de collège contient tous les éléments pour déterminer ce lieu des points (en dehors du langage des vecteurs).
ABCD est un rectangle de côtés 3 cm et 4 cm.
Quel est le rayon de son cercle circonscrit ?
ABCD est un rectangle de côtés a sur b.
Quel est le rayon de son cercle circonscrit ?
Dans un cercle de diamètre 13 cm, on trace un triangle rectangle dont l’un des côtés mesure 5 cm.
a. Faire la figure
b. Quelle est l’aire de ce triangle rectangle ?

Le théorème de Pythagore permet aussi d’entrer dans le calcul littéral.
Quelle est l’image du point B par la translation qui transforme A en D ?
Quelle est l’image du point B par la translation de vecteur \(\overrightarrow{AD}\) ?
Que peut-on dire lorsqu’on a \(\overrightarrow{GH}=\overrightarrow{HK}\) ?
Le point O est le milieu de [AC].
a. Caractériser vectoriellement : O est le milieu de [AC].
b. Quelle est l’image du point A par la translation de vecteur \(\overrightarrow{AO}\) ?
c. Quelle est l’image du point 0 par la translation de vecteur \(\overrightarrow{AO}\) ?
d. Que peut-on dire des vecteurs \(\overrightarrow{AO}\) et \(\overrightarrow{OC}\) ?

L’effet d’une translation aura été vue en cycle 4 de collège. L’utilisation de vecteurs est une nouveauté de seconde.
Remarque : dans les « Repères annuels de progression de Cycle 4 », en 4e : La définition ponctuelle d’une translation ne figure pas au programme. Toutefois, par commodité, la translation transformant le point A en le point B pourra être nommée « translation de vecteur \(\overrightarrow{AB}\) », mais aucune connaissance n’est attendue sur l’objet « vecteur ».
On a un point A fixe et on définit un point M tel que MA = 2.
Où sont situés les points M possibles ?
On a un point A fixe et on définit un point M tel que MA = k, où k est un nombre positif.
Où sont situés les points M possibles ?
Que peut-on dire du vecteur \(\overrightarrow{AA}\) .

Retour à la définition d’un cercle dans le plan.
Compréhension de ce que représente un vecteur nul.
Factoriser x×2+3×x
Factoriser (x+3)(3x-7)+(2x+5)(x+3)
Factoriser A×(5x+2)+(6x+1)×A

- Par ailleurs, la démonstration avec les vecteurs demandera aussi des connaissances et compétences en factorisation. Il s’agira de transposer les connaissances du calcul littéral vers du calcul vectoriel.
- On peut aussi prévoir de compléter en seconde avec « le point de concours des médiatrices est le centre du cercle circonscrit ». A noter qu’écrit comme cela, il y a un implicite qui est que l’on travaille dans un triangle. C’est cependant un exercice intéressant réactualisant l’équidistance.

En classe de première

Dans le programme :
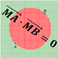
Ensemble des points M tels que \(\overrightarrow{MA}\cdot\overrightarrow{MB}=0\) (Démonstration avec le produit scalaire).

Le critère d’orthogonalité a été vu.

De même que \(\overrightarrow{0}\cdot\overrightarrow{u}=0\)

- S’assurer de quelques prérequis dans la progression
- Un travail de conjecture peut être mené avec un appui sur un logiciel de géométrie dynamique ou un programme en langage Python.
[fichiers produit_scalaire.py et produit_scalaire_lieu_auto.ggb]

Répertoire de votre page html.
Fait avant d’entamer ce travail, par exemple en Questions Flash (QF) :

Distance entre deux points dans un repère orthonormé, déterminer la longueur AB dans chacune des situations suivantes :
- A(0 ; 6) et B(0 ; 9)
- A(7 ; 0) et B(-10 ; 0)
- A(2 ; 7) et B(5 ; 3)
- A(1 ; 2) et B(6 ; 9)
l’équation d’un cercle : \(MI=rayon\) d’où \(MI^2 = rayon^2\) soit \(x^2+y^2=r^2\)
Ou \((x-x_i )^2+(y-y_i )^2=r^2\)
Calculs de coordonnées du milieu quand on dispose des coordonnées de deux points du plan.
A(2 ; 5) et B(8 ; 7) : déterminer les coordonnées de K milieu de [AB].
Détermination de la forme canonique :
- \(x^2-10x+16\)
- \(x^2-12x+35\)
- \((x-2)(x-8)\)

Le sens en lien avec ce qui a été vu précédemment (en cycle 4 et 2nde). [Pour tous les élèves]

M distinct de A et de B : MAB est un triangle rectangle en M, donc M est situé sur le cercle de diamètre [AB], sauf en A et en B.

Cas particulier : M est en A (ou en B) et le vecteur nul.

- Raisonnement par disjonction de cas.
- Caractérisation d’un triangle rectangle.
Objectif : Amener à partir de plusieurs exemples génériques (en groupe) afin de faire émerger le cas général.
La différenciation peut se faire en termes de démonstration de la méthode générale.

Dans un repère orthonormé, on a A(2 ; 5) et B(8 ; 7) et on note M(x ; y).
Puis on travaille sur \(\overrightarrow{MA}\cdot\overrightarrow{MB}=0\) afin d’obtenir une équation de cercle dont le centre est le milieu de [AB].

Cadre : repère orthonormé
- Travail sur le second degré (recherche de formes canoniques)
- La définition analytique du produit scalaire
- Identification des coordonnées du milieu ou retour à la distance entre deux points
Objectif : Construire des images mentales sur le lien entre produit scalaire et mesure d’angle en exploitant les diverses représentations du produit scalaire des élèves (projection, cosinus notamment).

Soit ABC un triangle tel que \( \widehat{ABC}=20°\) et \( \widehat{ACB}=120°\). Quel est le signe des produits scalaires suivants :
* \(\overrightarrow{AB}\cdot\overrightarrow{AC}\)
* \(\overrightarrow{BA}\cdot\overrightarrow{BC}=0\)
* \(\overrightarrow{CA}\cdot\overrightarrow{CB}=0\)

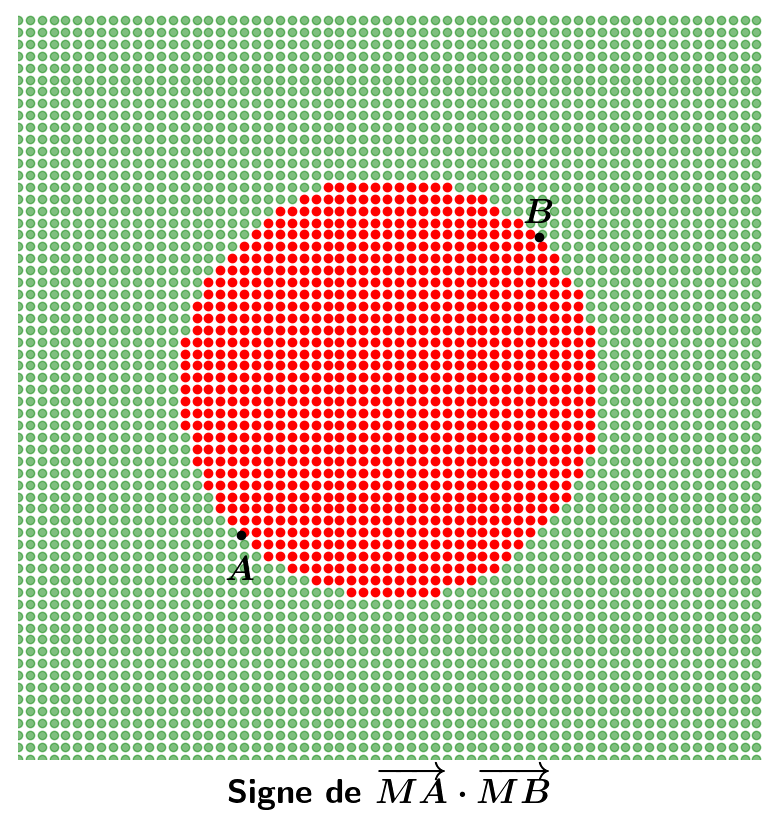
Possibilité de conjecturer avec Geogebra par exemple sur le problème suivant (version de la situation de Brousseau sur la caractérisation des triangles AMB rectangle en M mais avec les produits scalaires) :
« Soient A et B deux points fixés. Où sont situés les points M tels que \(\overrightarrow{MA}\cdot\overrightarrow{MB}<0\) . »
Le sens avec un travail sur les vecteurs : \(\overrightarrow{MA}\cdot\overrightarrow{MB}=0\) avec le produit scalaire (à aborder dans le cadre de la différenciation)
\(\overrightarrow{MA}\cdot\overrightarrow{MB}=0\)
\((\overrightarrow{MI} +\overrightarrow{IA}) \cdot(\overrightarrow{MI} +\overrightarrow{IB})=0\)
Puis travail sur \(\overrightarrow{MI} \cdot\overrightarrow{IB}+\overrightarrow{IA} \cdot\overrightarrow{MI}\) et sur\(\overrightarrow{IA} \cdot\overrightarrow{IB}\).

Travail sur la factorisation puis le vecteur nul : passe à \(– IA^2\) soit \(– rayon^2\).
Pour arriver à \(MI^2 = rayon^2\)

- Caractérisation vectorielle de I milieu de [AB]
- Calcul vectoriel (relation de Chasles)
- Utilisation des propriétés du produit scalaire (symétrie et bilinéarité)
- Factorisation
- Définition d’un cercle via la distance