espace pédagogique > disciplines du second degré > mathématiques > enseignement > activités pédagogiques
rentrée 2020 - Focus 2nde
mis à jour le 15/09/2020
Priorités pédagogiques et outils de positionnement pour la période septembre-octobre pour la classe de 2nde : probabilités.
mots clés : priorités pédagogiques, probabilité
Le document de rentrée 2020 pour la classe de 2nde en mathématiques précise :
« Statistiques et probabilités
- Travailler rapidement sur les proportions, en passant des contenus de troisième (quatrième proportionnelle) aux contenus de seconde (information chiffrée et statistique descriptive)
- En probabilités, aborder les contenus de seconde en travaillant sur des exemples simples et en explicitant la situation, le modèle et le vocabulaire. »
Concernant les probabilités en collège
Dans les attendus de fin d’années du cycle 4, il est indiqué « Ce que sait faire l’élève » :
- attendus de fin de 5e
- Il place un événement sur une échelle de probabilités.
- Il calcule des probabilités dans des situations simples d’équiprobabilité.
- attendus de fin de 4e
- Il utilise le vocabulaire des probabilités : expérience aléatoire, issues, événement, probabilité, événement certain, événement impossible, événement contraire.
- Il reconnaît des événements contraires et s’en sert pour calculer des probabilités.
- Il calcule des probabilités.
- Il sait que la probabilité d’un événement est un nombre compris entre 0 et 1.
- Il exprime des probabilités sous diverses formes.
- attendus de fin de 3e
- À partir de dénombrements, il calcule des probabilités pour des expériences aléatoires simples à une ou deux épreuves.
- Il fait le lien entre stabilisation des fréquences et probabilités.
Concernant les probabilités en classe de 2nde
 « Modéliser le hasard, calculer des probabilités »
« Modéliser le hasard, calculer des probabilités » Dans le programme de la classe de 2nde, les capacités attendues sont :
- Utiliser des modèles théoriques de référence (dé, pièce équilibrée, tirage au sort avec équiprobabilité dans une population) en comprenant que les probabilités sont définies a priori.
- Construire un modèle à partir de fréquences observées, en distinguant nettement modèle et réalité.
- Calculer des probabilités dans des cas simples : expérience aléatoire à deux ou trois épreuves.
Des questions possibles dans un rituel de type questions flash :
- Classer les probabilités suivantes de la plus improbable à la plus probable :
0,45 ; 0,8 ; 0,09 ; 0,65 ; 0,95 - L’expérience consiste à lancer un dé numéroté de 1 à 6. Le modèle d’équiprobabilité est-il valide ?
- L’expérience consiste à lancer deux dés numérotés chacun de 1 à 6 et on s’intéresse à la somme des deux valeurs obtenues. Le modèle d’équiprobabilité est-il valide ?
- L’expérience consiste à lancer deux dés numérotés chacun de 1 à 6, un dé bleu et un dé rouge.
- On s’intéresse au quotient
.
- Quelle est la probabilité d’obtenir un quotient entier ?
- Quelle est la probabilité d’obtenir un quotient décimal ?
- Quelle est la probabilité d’obtenir un quotient rationnel non décimal ?
- L’expérience consiste à lancer deux dés classiques numérotés chacun de 1 à 6 et on s’intéresse au produit des deux valeurs obtenues.
- Donner un événement certain associé à cette expérience.
- Donner un événement impossible associé à cette expérience.
- L’expérience consiste à lancer deux dés classiques numérotés chacun de 1 à 6 et on s’intéresse au produit des deux valeurs obtenues.
- Quelle est la probabilité d’obtenir 1 ?
- Quelle est la probabilité d’obtenir 6 ?
- Quelle est la probabilité d’obtenir 11 ?
- Il y a 8 filles et 17 garçons dans un groupe.
L’expérience consiste à choisir au hasard une personne de ce groupe. Parmi les affirmations suivantes, déterminer celles qui sont vraies, celles qui sont fausses et celles pour lesquelles on ne peut pas savoir.- Il est plus probable de choisir un garçon qu’une fille.
- La probabilité de choisir une fille est plus de 1/2 que de 1/3.
- La probabilité de choisir un garçon est 0,68.
- « Choisir une personne de 16 ans » est un événement certain.
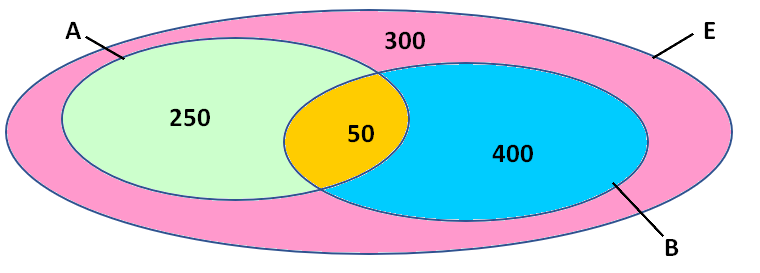
- Ce diagramme représente la répartition de 1 000 éléments d’un ensemble E.
L’expérience consiste à prendre au hasard un élément de E. Quelle est la probabilité que cet élément appartienne à
information(s) pédagogique(s)
niveau : 2nde
type pédagogique :
public visé : non précisé
contexte d'usage :
référence aux programmes :
ressource(s) principale(s)

|
rentrée 2020 | 15/09/2020 |
| Priorités pédagogiques et outils de positionnement pour la période septembre-octobre | ||
| priorités pédagogiques | ||
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA