Contenu

mathématiques

Recherche simple Vous recherchez ...

espace pédagogique > disciplines du second degré > mathématiques > enseignement > activités pédagogiques

rentrée 2020 - Focus 4e

mis à jour le 15/09/2020


2020-4.png

Priorités pédagogiques et outils de positionnement pour la période septembre-octobre pour la classe de 4e : comprendre et utiliser la notion de fonction.

mots clés : priorités pédagogiques, notion de fonction

Les ressources publiées sur ce site sont sous la licence CC BY-NC 4.0.
 

Le document « priorités maths 4e » précise :
  • L'élève reconnaît une situation de proportionnalité ou de non proportionnalité entre deux grandeurs.
  • Il résout des problèmes de proportionnalité, notamment en utilisant des pourcentages ou des échelles.
  • L'élève comprend et utilise la notion de fonction ; il traduit la dépendance entre deux grandeurs par un tableau de valeurs ; il produit une formule représentant la dépendance entre deux grandeurs.

Concernant la proportionnalité et les fonctions :
Les repères annuels de cycle 4 indiquent pour les classes de 5e, 4e et 3e (de gauche à droite dans le tableau) – en vert, ce qui est à réactiver ou à consolider– en rouge, ce qui est à construire durant l'année de 4e :

Point essentiel pour la formation des élèves :
Il ne s'agit pas de formaliser ou de traiter l'ensemble des éléments sur les fonctions mais bien de profiter de ce début d'année pour réactiver ou construire des représentations. Faire vivre en classe des situations mobilisant des changements de cadre (dépendance de grandeurs, tableau de valeurs, formules, graphiques) dès le début de l'année permet de construire sur un temps long la notion de fonction.

Par ailleurs, les « attendus de fin de 4e » indiquent « ce que sait faire l'élève » :
  • Il produit une formule littérale représentant la dépendance de deux grandeurs.
  • Il représente la dépendance de deux grandeurs par un graphique.
  • Il utilise un graphique représentant la dépendance de deux grandeurs pour lire et interpréter différentes valeurs sur l'axe des abscisses ou l'axe des ordonnées.

Un travail sur les graphiques a pu être mené dès la classe de 6e. Il est possible de le poursuivre, en rituels de type questions flash par exemple dès le début de l'année.
La notion de dépendance entre deux grandeurs ou la production de formules littérales auront été plus récemment abordées, en particulier en début de cycle 4.

Outre des questions flash (par exemple des questions du type questions 5 à 10 du focus 5e, ou encore des questions choisies parmi celles proposées dans « une progression autour de l'algèbre en classe de 4e »), les élèves peuvent travailler la fabrication d'expressions.

Les questions proposées dans ce document peuvent parfois être facilement abordées lors de questions flash, et seront signalées par le logo ci-contre.
Les autres peuvent faire l'objet d'un temps court sur une séance.
 
Petite fabrique d’expressions
Exercice 1
ABCD est un carré de côté 3 cm.
  1. Quel est le périmètre de ce carré ?
  2. Quelle est l’aire de ce carré ?
On dispose à côté de ce carré un deuxième carré identique. On obtient alors le rectangle ADEF.
  1. Quel est le périmètre de ce rectangle ?
  2. Quelle est l’aire de ce rectangle ?
On dispose à côté un certain nombre de carrés…On obtient alors un « long rectangle ».
  1. Exprimer le périmètre de ce rectangle.
  2. Exprimer l’aire de ce rectangle.
  3. Le périmètre peut-il être égal à 1 m ?




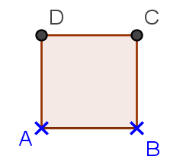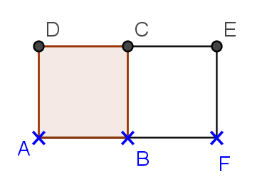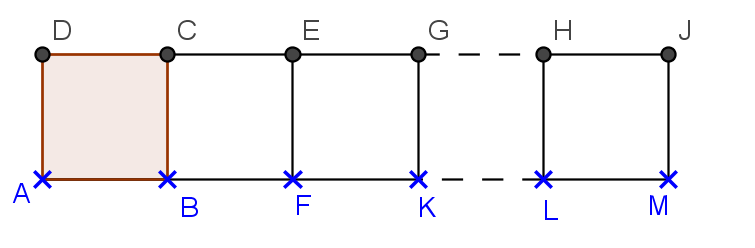Exemple d’un bilan en classe
  • L’introduction de la lettre est progressive.
  • Le passage de 9×n à 9n également.
  • La notation pn ou An nécessite quelques précautions, et là aussi s’introduit, si cela est adapté à la classe, peu à peu.
    Cela peut tout à fait rester sous la forme
    pn = …
    An = …
    ou encore
    périmètre = …
    Aire = …
  • Le fait d’écrire une phrase avec une formulation du type « varie en fonction de » n’oblige pas à utiliser la notation de type f(x), qui pourra est présentée uniquement en 3e.

Exercice 2
  1. Appliquer chacun des programmes de calculs aux nombres : 0 ; 1 et 2.
  2. Pour quelle(s) valeur(s) de départ ces deux programmes donnent-ils la même valeur à l’arrivée ?

Exercice 3
La figure de base ci-contre est constituée du rectangle ABCD et du carré CDFE.

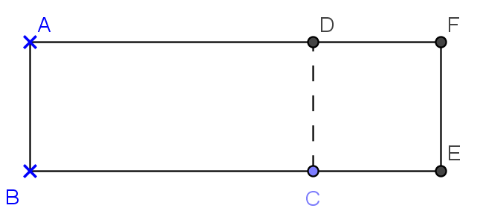
1ère partie : dans cette partie, AB = 5 cm et AD peut varier.
  1. Exprimer le périmètre du rectangle ABEF.
  2. Exprimer l’aire du rectangle ABEF.
  3. On construit un « long rectangle » en disposant côte à côte un certain nombre de figure de base.
    • Exprimer le périmètre de la figure ainsi obtenue.
    • Exprimer l’aire de la figure ainsi obtenue
  
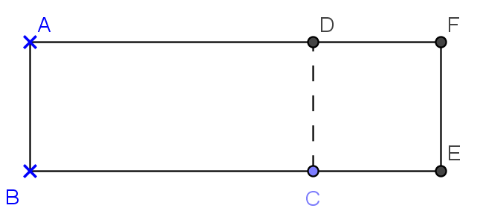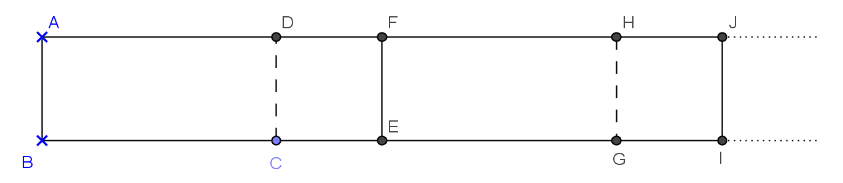2ère partie : dans cette partie, AD = 7 cm et AB peut varier.
  1. Exprimer le périmètre du rectangle ABEF.
  2. Exprimer l’aire du rectangle ABEF.
  3. On construit un « long rectangle » en disposant côte à côté un certain nombre de figure de base.
    • Exprimer le périmètre de la figure ainsi obtenue.
    • Exprimer l’aire de la figure ainsi obtenue.
  


 

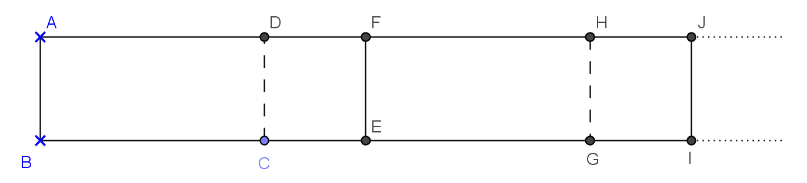information(s) pédagogique(s)

niveau : Cycle 4, 4ème

type pédagogique :

public visé : non précisé

contexte d'usage :

référence aux programmes :

ressource(s) principale(s)

2020.png rentrée 2020 15/09/2020
Priorités pédagogiques et outils de positionnement pour la période septembre-octobre
priorités pédagogiques

haut de page

mathématiques - Rectorat de l'Académie de Nantes