mathématiques

espace pédagogique > disciplines du second degré > mathématiques > enseignement > activités pédagogiques

Signe d'une expression

mis à jour le 15/05/2008

Il s'agit d'utiliser le signe d'une expression en laissant l'initiative aux élèves . Cela permet de différencier le travail car les prolongements possibles sont nombreux. Après, on pourra introduire les tableaux de signes pour les cas les plus compliqués.

mots clés : signe, produit, quotient, tableur, expérimentation, validation

Enoncé

On considère le nombre N = (2x + 3) (4 - x). On veut connaître son signe pour toute valeur de x dans IR.

A l'aide d'un brouillon et/ou de tout matériel mis à votre disposition, que pouvez-vous observer ou affirmer concernant le signe de N ?
Prendre des notes sur toute démarche que vous tentez, qu'elle aboutisse ou non.
Démontrer ce que vous avez conjecturé.

Objectifs

L'objectif essentiel est la détermination du signe d'un produit (puis d'un quotient dans une autre séance) et l'introduction de l'outil tableau de signe dans les cas les plus compliqués à gérer (par exemple pour le signe d'un produit de trois facteurs). Il s'agit aussi de mettre en place une interprétation graphique des résultats.
Les autres objectifs sont de reparler des fonctions affines (sens de variation), des droites (coefficient directeur), du signe d'une fonction (lecture graphique), de la résolution d'une inéquation du 1er degré à une inconnue et d'une équation-produit nulle.
Un dernier objectif est de se confronter à l'usage d'un logiciel ou du choix du menu de sa calculatrice adapté à sa démarche.

Scénario

En seconde, cette activité s'est déroulée, dans un premier temps, en demi-classe pendant un module. Chaque élève avait à sa disposition un poste informatique équipé d'un tableur (Excel), d'un grapheur (Archimède) et pouvait utiliser sa calculatrice graphique.
La synthèse des démarches a été faite en classe entière, à l'aide d'un vidéoprojecteur.

Le déroulement

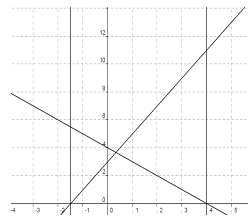
Les élèves, sans indication de ma part, ont pris individuellement différentes initiatives :

Utilisation d'un grapheur ou de la calculatrice, pour tracer la courbe représentative de la fonction f définie sur par
Utilisation d'un tableur pour fabriquer une table de valeurs puis un graphique.
Certains effectuent quelques calculs à la main puis réalisent une table de valeurs avec la calculatrice pour accéder à plus de tests.
Utilisation complémentaire ou simultanée d'un grapheur et d'un tableur
Résolution de l'équation-produit nulle pour rechercher les intervalles où le changement de signe de N pouvait s'opérer.
Recherche de la 2ème valeur (non entière) qui annule N, par balayage dans le tableur de la calculatrice.
Résolution des inéquations du 1er degré séparément (recherche du signe de chaque facteur)

Intervention auprès de quelques élèves

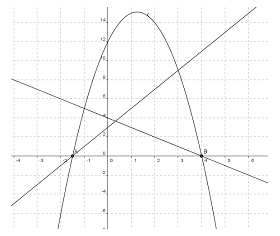
L'obtention du graphique a permis de se poser la question suivante : est-on sûr que la courbe ne franchit pas de nouveau l'axe des abscisses en changeant de variations plusieurs fois ?

C'est la résolution de l'équation-produit qui a permis d'affirmer que la courbe ne franchissait l'axe des abscisses en deux points seulement et que même si les variations changeaient, le signe de N lui ne changerait pas (sauf discontinuité de la fonction).
L'utilisation du grapheur Archimède, de sa fonction zoom et de l'ascenseur, ont permis de « voir » cette non-discontinuité et les variations.

Une initiative originale

Lors de l'année scolaire précédente, un élève a eu la bonne idée de tracer le graphique ci-contre représentant les deux fonctions affines associées à chaque facteur.
Il a alors commencé à décliner tous les cas en travaillant par intervalle et en partageant le plan du repère par les droites d'équation x = - 1,5 et x = 4, puis de construire dessous ce graphique un tableau de signes.
De plus la superposition avec la courbe représentant f a permis de contrôler sa démarche.

Remarques

Face à toutes ces initiatives, la mise en commun est plus que nécessaire après la recherche. Je n'ai pas souhaité interrompre leurs initiatives pour les orienter sur une stratégie plutôt qu'une autre. Mon objectif a été plutôt de valoriser leurs démarches et de les aider à progresser en les questionnant chaque fois que cela était possible pour les débloquer. Cela a permis à presque tous les élèves de déterminer le signe de N suivant les valeurs de x, le calcul algébrique étant plus rebutant pour les élèves que l'aspect graphique et l'utilisation des TICE.

L'élaboration du tableau de signe s'est faite à partir du graphique et son utilité « prouvée » en montrant les limites de la résolution algébrique s'il s'agissait d'un produit de 3 facteurs (nombre de cas multiplié par 2), cette problématique a été posée à un élève comme extension et généralisation de l'activité précédente.

Compétences expérimentales

Prendre l'initiative d'utiliser un tableur pour réaliser une feuille automatisée de calcul.
Réaliser des tests automatisés avec un tableur.
Prendre l'initiative de faire une analyse critique de l'outil utilisé (représentation graphique et changement du pas dans le tableur)
Faire une analyse comparative de plusieurs résultats (tableaux et graphiques)
Organiser une recherche (produit nul, recherche par intervalle)
Enoncer clairement une conjecture.
Choisir l'outil approprié pour sa démarche
Valider l'expérimentation en modifiant un paramètre (3 facteurs, facteur plus compliqué : zéro rationnel, voire irrationnel).
Prendre l'initiative de vérifier un résultat.
Etre capable de « rebondir », savoir débloquer une situation en utilisant une nouvelle idée.

Prolongements possibles

Quatre types de prolongements pourraient être envisagés (voir en annexe):

Généraliser le même type d'activité avec des expressions formées du produit d'au moins trois facteurs : l'organisation des résultats devient plus compliquée et l'outil « tableau de signe » devient pertinent.
Confronter l'élève à des cas où il n'y a pas alternance entre + et -
Proposer une étude du signe d'un produit à partir des représentations graphiques de chacun des facteurs (sans disposer de l'écriture algébrique).
Etudier le signe d'un quotient.

auteur(s) :

Pascal Bardaud