espace pédagogique > disciplines du second degré > physique chimie > enseigner > ressources documentaires
à la découverte des ondes
mis à jour le 13/04/2012
Cette activité a pour but d'initier la réflexion sur l'existence des ondes dans de nombreux domaines de notre vie quotidienne. Elle permet de réinvestir les connaissances de la classe de première sur les ondes électromagnétiques.
mots clés : propagation, oscillation, fréquence, mécanique, électromagnétique, sonore, sismique
D'après le magazine « Pour la Science », Numéro Spécial - Novembre 2011 - N°409
Extrait du texte de Claude Bardos, Mathématicien, professeur émérite à l'Université Paris 7.
Il est membre du Laboratoire Jacques-Louis Lions à l'Université Pierre et Marie Curie à Paris.
« Malgré leur diversité, les ondes constituent un phénomène physique universel. Leur description et leur compréhension sont liées aux grandes avancées de la physique et des mathématiques.
1.1 Diversité des ondes
Les ondes sont présentes partout autour de nous et ont été observées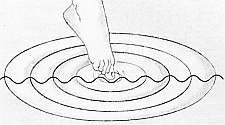 bien avant l'avènement de la science moderne. Sous leur forme probablement la plus évidente, ce sont les rides circulaires créées à la surface d'un étang par la chute d'un petit caillou, les vagues de l'océan créées par le vent, les marées dues à l'attraction du Soleil et de la Lune, les mascarets qui remontent les fleuves, etc.
bien avant l'avènement de la science moderne. Sous leur forme probablement la plus évidente, ce sont les rides circulaires créées à la surface d'un étang par la chute d'un petit caillou, les vagues de l'océan créées par le vent, les marées dues à l'attraction du Soleil et de la Lune, les mascarets qui remontent les fleuves, etc.
De fait, le mot onde provient du latin unda, qui signifie eau courante, ce qui souligne la proximité de la notion d'onde avec le phénomène constatée sur des étendues d'eau. La langue anglaise n'a d'ailleurs qu'un seul et même mot ( wave ) pour désigner une onde et une vague.

D'autres types d'ondes sont faciles à remarquer, comme celles qui parcourent une corde que l'on agite à l'une de ses extrémités (voir ci-contre). Mais les ondes prennent souvent des formes moins visibles : les sons, la lumière, les tremblements de terre, sont aussi des phénomènes ondulatoires. Les sons mettent en jeu des ondes de pression se propageant dans l'air, la lumière des ondes de vibrations du champ électromagnétique se propageant dans le vide, les tremblements de terre des ondes mécaniques se propageant dans le sol. Á un niveau plus fondamental encore, la physique quantique associe à la matière et à ses interactions des ondes de nature abstraite, mais indispensable à la description et à la compréhension des phénomènes.
Enfin, les ondes, qu'elles soient électromagnétiques ou autres, tiennent une place capitale dans les technologies modernes, comme en témoignent la télévision, les radars, la téléphonie mobile, la radiographie médicale ou industrielle, les fours à micro-ondes, l'échographie, etc.
L'histoire de l'étude des ondes se confond assez largement avec celle de la physique et des mathématiques. Si Pythagore et son école, vers le Ve siècle avant notre ère, ont mis en évidence des rapports numériques portant sur les cordes vibrantes et les sons musicaux, une véritable science des ondes n'est apparue qu'avec la naissance de la science moderne, à l'époque de Galilée et de Newton, aux XVIe et XVIIe siècles. Le premier domaine concerné fut l'acoustique, avec Galilée et le père Marin Mersenne. En particulier, Galilée a relié le « nombre de vibrations » d'une corde à sa longueur, à sa masse et à sa tension, ainsi qu'au son plus ou moins aigu qu'elle produit. Quant à Mersenne, pionnier de l'acoustique, il fut le premier à évaluer la vitesse du son, dont il avait une conception ondulatoire.
La nature de la lumière a donné davantage de soucis aux physiciens. Malgré certaines de ses expériences qui s'interprètent plus facilement en termes d'ondes, Newton considérait la lumière comme un ensemble de corpuscules. D'autres savants, comme le jésuite Francisco Maria Grimaldi (1618 - 1663), défendaient une conception ondulatoire. Le débat s'est prolongé jusqu'au début du XVIIIe siècle, lorsque la balance a penché du côté de l'onde grâce notamment à la théorie proposée en 1815 par le physicien français Augustin Fresnel. Et en 1864, l'ecossais James Clerk Maxwell unifia en un seul ensemble d'équations ( qui portent son nom ) l'électricité, le magnétisme, l'induction électromagnétique et la théorie ondulatoire de la lumière - ce fut une étape cruciale du développement de la physique théorique.
Dans les équations de Maxwell, la vitesse de la lumière apparaît comme une constante absolue, indépendante de l'observateur et de ce fait contradictoire avec le principe de la relativité de la physique galiléenne et newtonienne. C'est ce qui a conduit Einstein à sa théorie de la relativité restreinte, publié en 1905. Par un curieux retour des choses, Einstein est aussi celui qui a montré clairement que l'énergie lumineuse est transportée par quantités bien définies, des « quanta » qu'on appela plus tard photons, ce qui représentait un retour - partiel - de la conception corpusculaire de la lumière. Et Einstein a participé à l'émergence de la physique quantique, où la notion d'onde intervient au niveau le plus fondamental.
1.2 Oscillation et propagation
Ce rapide survol de plus de trois siècles ne rend pas justice aux efforts des physiciens, aux débats qui les ont agités, aux découvertes intrigantes ou surprenantes qu'ils ont faites. Toujours est-il que les ondes ont occupé dans cette histoire une place de choix. Elles ont aussi grandement stimulé les mathématiciens. L'étude des ondes a en effet nécessité l'élaboration d'outils de plus en plus puissants et complexes, ce qui a contribué au développement des mathématiques depuis Newton et Leibniz jusqu'à nos jours. Je vais présenter ici certains de ces développements en relation avec les ondes, car ils aident à comprendre ce qu'est une onde et ce que ce concept a de si universel.
1.3 Qu'est-ce qu'une onde ?
Il est difficile de donner une réponse univoque à cette question. On peut dire que le terme onde désigne la propagation, de proche en proche, d'une variation à laquelle est soumise une certaine grandeur physique. [...] . La variation qui se propage prend souvent la forme d'une oscillation, d'une vibration. De fait, l'oscillation et la propagation sont deux aspects complémentaires et pratiquement indissociables de la notion d'onde.
Pour comprendre ce qu'est une onde et comment on la décrit mathématiquement, commençons par la description d'une oscillation simple : l'oscillation de l'extrémité d'un ressort de part et d'autre de sa position d'équilibre ( voir figure ci-dessous ). On suppose pour simplifier que le ressort, de masse négligeable est posé sur un plan horizontal sans frottement, avec une masse m attachée à son extrémité.
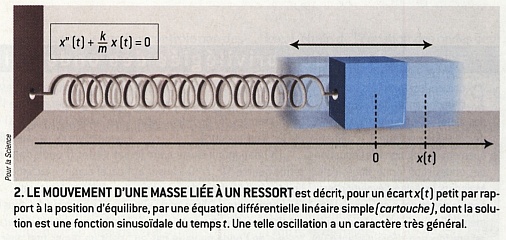
Désignons par x(t) la position, qui dépend du temps t, de cette masse par rapport à sa position d'équilibre. Si cet écart x(t) est petit, alors la force de rappel du ressort vers la position d'équilibre est, en première approximation, proportionnelle à l'écart. Autrement dit, sa valeur algébrique est -k.x(t), où k est une constante positive appelée la raideur du ressort.
D'après la deuxième loi de Newton, la force appliquée à un mobile est égale au produit de sa masse par son accélération. Dans notre cas, cela s'écrit : -k.x(t) = m.x''(t), où x''(t) est la dérivée seconde de x(t). En posant 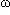 2 = k/m, on obtient que le mouvement de l'extrémité du ressort obéit à l'équation différentielle x''(t) +
2 = k/m, on obtient que le mouvement de l'extrémité du ressort obéit à l'équation différentielle x''(t) + 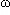 2.x(t) = 0.
2.x(t) = 0.
On montre que cette équation élémentaire a pour solution générale : x(t) = a.cos(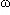 t) + b.sin(
t) + b.sin(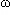 t), où a et b sont des constantes déterminées de façon unique par les conditions initiales, c'est-à-dire par la donnée de la position et de la vitesse du mobile à l'instant initial t = 0 s ( ou à tout autre instant fixé ). Cette solution est périodique, la période T étant égale à 2
t), où a et b sont des constantes déterminées de façon unique par les conditions initiales, c'est-à-dire par la donnée de la position et de la vitesse du mobile à l'instant initial t = 0 s ( ou à tout autre instant fixé ). Cette solution est périodique, la période T étant égale à 2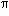 /
/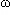 ; la fréquence f de l'oscillation est l'inverse de la période ( f = 1/T ), tandis que
; la fréquence f de l'oscillation est l'inverse de la période ( f = 1/T ), tandis que 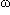 est la « pulsation » de l'oscillation, qui est proportionnelle à sa fréquence (
est la « pulsation » de l'oscillation, qui est proportionnelle à sa fréquence (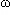 = 2
= 2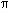 f ). Elle est même sinusoïdale, puisque a.cos(
f ). Elle est même sinusoïdale, puisque a.cos(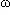 t) + b.sin(
t) + b.sin(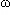 t) s'écrit aussi sous la forme A.cos(
t) s'écrit aussi sous la forme A.cos(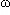 t +
t + 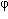 ), où les constantes A et
), où les constantes A et 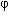 se calculent à partir de a et b.
se calculent à partir de a et b.
[...]
L'univers des ondes est un univers foisonnant. Les ondes interviennent sous une forme ou une autre dans presque tous les phénomènes physiques. Liant oscillation et propagation, avec des effets de dispersion et des non-linéarités qui augmentent d'autant leur complexité et leur richesse, elles sont fondamentales pour les physiciens et les ingénieurs. L'étude des ondes a aussi été un stimulant essentiel de plusieurs champs des mathématiques. Elle l'est toujours. »
Claude Bardos
2.1 Pistes d'exploitation possibles
- D'après l'auteur, une onde désigne : « la propagation, de proche en proche, d'une variation à laquelle est soumise une certaine grandeur physique ».
Quelle grandeur physique varie dans les 3 cas suivants ?
- Onde créée par la chute d'un caillou dans un étang.
- Onde sonore créée par une corde de guitare.
- Oscillation d'une masse attachée à un ressort. - L'échographie utilise-t-elle une onde électromagnétique ou une onde sonore ?
Même question pour la téléphonie mobile. - « Einstein a participé à l'émergence de la physique quantique, où la notion d'onde intervient au niveau le plus fondamental ».
Rappeler la relation vue en classe de première permettant de calculer l'énergie E d'un photon de fréquence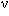 .
. - Utiliser cette relation pour calculer la fréquence du photon émis lorsqu'un atome passe de l'état d'énergie E1 = - 3,03 eV à l'état d'énergie E0 = - 5,14 eV. On donne : 1 eV = 1,60x10-19 J.
Cette onde électromagnétique est-elle visible ? - Recopier et compléter le tableau ci-dessous :
Savants ayant défendu une idée corpusculaire de la lumière Savants ayant défendu une idée ondulatoire de la lumière - En quelle unité s'exprime une force ? En déduire l'unité de k, constante de raideur d'un ressort.
- « la fréquence f de l'oscillation est l'inverse de la période ( f = 1/T ) » ; proposer une autre définition de la fréquence.
- Utiliser la relation
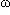 = 2
= 2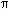 f pour en déduire l'unité de la pulsation.
f pour en déduire l'unité de la pulsation.
information(s) pédagogique(s)
niveau : Terminale S
type pédagogique : scénario, séquence, exercice
public visé : élève
contexte d'usage : classe, travail autonome
référence aux programmes :
Thème : OBSERVER, Ondes et matière : Ondes et particules
Compétences travaillées ou évaluées :
- Extraire et exploiter des informations sur les manifestations des ondes mécaniques dans la matière.
- Manifester sa compréhension d'un texte documentaire.
- Enrichir le vocabulaire.
- Dégager les idées essentielles d'un texte.
- Rechercher, extraire et organiser l'information utile.
- Répondre à une question par une phrase complète.
- Communiquer et travailler en équipe.
fichier joint
information(s) technique(s) : Fichier modifiable au format . docx
taille : 457 kio ;
ressource(s) principale(s)

|
ressources pour le programme 2012 de Terminale S - observer - ondes et matière | 11/07/2011 |
| les productions nouvelles pour le programme 2012 sur le thème « observer : ondes et matière » . | ||
| réforme, terminale,TS | ||
physique chimie - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA
