espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > actions nationales 2015-2017 > 2 séances ou 3
la fourmi de Langton
mis à jour le 17/05/2016
mots clés : algorithmique, TraAM
Objectif
L'objectif est de faire étudier aux élèves un algorithme simple à comprendre mais dont la mise en œuvre informatique peut être un peu complexe. Ce travail permettra également de retravailler la condition. C'est aussi l'occasion d'enrichir leur culture mathématique.
Pour les élèves les plus rapides, des variations de l'algorithme sont proposées.
Déroulement de la séance :
L'activité est proposée à une classe de 4e qui a déjà travaillé avec Scratch. C'est leur 4e séance. Le travail est conçu pour être fait en 2 heures avec des temps clairement identifiés.
Temps n°1
Le point de départ de l'activité est un extrait d'une vidéo issue du blog « Sciences étonnantes » qui présente l'algorithme de la fourmi de Langton. Les élèves sont seuls ou en binôme devant un ordinateur.
Une feuille de consigne leur est distribuée. Le but de ce premier temps est de comprendre l'algorithme et d'arriver à produire sur une feuille la figure obtenue à la 15e étape, l'objectif étant de s'approprier l'algorithme.
Dans l'ensemble, l'algorithme simple est facilement compris mais le mettre en œuvre sur le papier est clairement plus difficile. Peu de binôme arriveront finalement à la figure correcte au bout d'une vingtaine de minutes. Il a été difficile de gérer l'alternance des couleurs et des directions. Cela nécessite d'être très rigoureux.
Un bilan est fait en classe entière pour s'assurer que tout le monde a bien compris et proposer la figure.
Temps n°2
Il s'agit de préparer la mise en œuvre de l'algorithme dans Scratch en réfléchissant aux briques et aux lutins nécessaires.
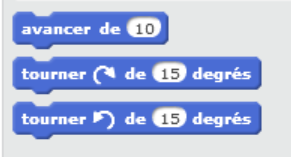
Cela a posé beaucoup de difficultés aux élèves qui se sont focaliser très rapidement sur quel lutin choisir pour faire la fourmi sans penser au reste. Après un rappel de la consigne et repréciser les attentes, certains binômes ont proposé la majorité des briques nécessaires, notamment celle sur la condition de couleur :
    |
Après un temps, la question de comment colorier une case s'est fait sentir et certains groupes ont pensé au stylo, un groupe a découvert la brique « estampiller ».
Certains groupes ont voulu avoir accès à un quadrillage mais aucun n'a pensé à ajouter de lutins qui auraient la forme de carré, ce qui est normal puisqu'ils ne connaissent que la brique stylo.
Un bilan est fait en classe entière afin de faire le point sur leur proposition. C'est aussi l'occasion pour moi de préparer la mise en place de l'algorithme dans Scratch et de leur fournir une aide sur la difficulté de la gestion de la couleur :
- Je leur présente le bloc estampiller et son rôle.
- Je leur indique donc qu'on peut créer deux lutins supplémentaires : un carré noir et un carré blanc et leur montre un exemple d'utilisation de la fonction « estampiller » avec ces deux lutins.
- Afin de lever certaines difficultés, je leur suggère l'utilisation des costumes et leur montre l'utilisation de la brique « basculer sur le costume »
- L'initialisation de l'algorithme leur est donné :
Temps n°3
Les élèves vont avoir à disposition dans leur espace de classe plusieurs images : un carré noir et un carré blanc de 10 × 10 pixels, un carré noir, un carré blanc et un carré rouge d'une taille de 6 × 6 pixels.
Les binômes sont laissés en autonomie pour programmer.
Deux binômes arrivent en une dizaine de minutes à programmer l'algorithme mais ils n'ont pas pensé à un détail : les carrés ne se touchent pas. Je leur indique et les laisse corriger.
Plusieurs binômes ont eu du mal à reproduire la situation de départ, notamment charger le lutin et son second costume.
La principal difficulté rencontrée est sur l'ordre dans lequel mettre les blocs à l'intérieur de la condition. En effet, l'algorithme a programmé est un peu différent de celui en langage naturelle, il faut colorier la case où on est avant de se déplacer. Cet aspect a posé quelques difficultés.
D'autres difficultés ont été rencontrées comme les changements de costumes, le pas duquel avancer.
Pour un élève en difficulté importante, le début du programme est fourni ainsi que tous les blocs à utiliser.
Quand les binômes ont terminé, plusieurs prolongements leur sont proposés :
Refaire la programmation avec des carrés de plus petite taille et d'observer la figure obtenue avec différents nombres d'itérations (300 puis 2000 et enfin 8500)
Refaire la programmation avec trois carrés suivant deux algorithmes différents comme proposés dans la consigne.
Quelques réalisations d'élèves
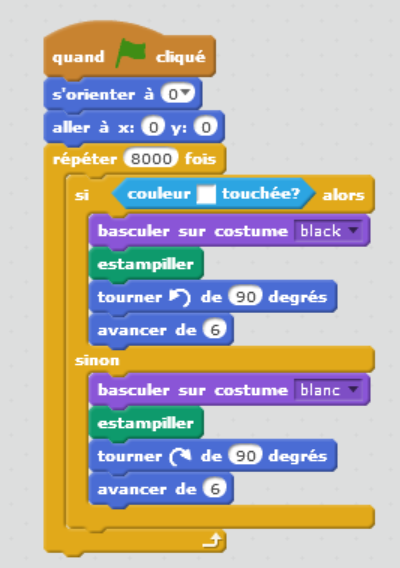 | 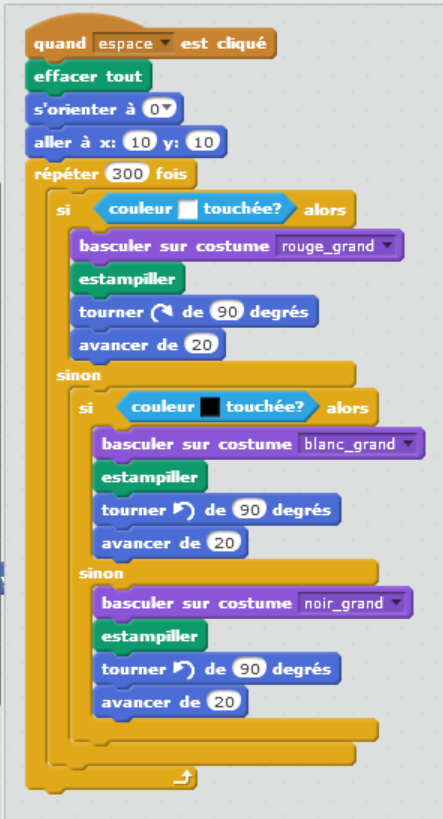 |
Conclusion et perspectives
Bien que la séance soit très guidée, notamment sur la mise en place de la programmation effective, plusieurs aspects intéressants ont émergé :
La difficulté pour de nombreux élèves a identifié de manière déconnecté les éléments nécessaires pour programmer l'algorithme. Il semble essentiel de proposer ce type d'activité, sur des algorithmes simples ou plus complexes, afin de mettre en place une vraie stratégie de raisonnement.
La prise de conscience de l'ordre des instructions et de la nécessité d'être rigoureux
Le travail sera prolongé en classe par la présentation du comportement de la fourmi avec un grand nombre d'itérations, de ce qui se passe avec 3 couleurs et la fin de la vidéo sera diffusée.
Grégory Maupu, Enseignant au Collège Charles Milcendeau - Challans (85)
information(s) pédagogique(s)
niveau : tous niveaux, Collèges tous niveaux, 4ème
type pédagogique :
public visé : non précisé, élève, enseignant
contexte d'usage : salle multimedia
référence aux programmes :
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA