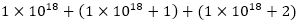espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > actions nationales 2015-2017 > 1 séance ou 2
somme de plusieurs entiers consécutifs
mis à jour le 11/05/2016
mots clés : algorithmique, TraAM, boucle, condition, modulo
Somme de 3 entiers consécutifs
| Sans consigne écrite les élèves doivent faire un programme qui permet de calculer la somme de 3 entiers consécutifs. Les élèves prennent connaissance des instructions qu’il est possible d’utiliser pour réaliser ce travail. D’autres sont possibles et toutes ne sont peut-être pas obligatoires. Les élèves savent comment décrire l’entier suivant : séance précédente. Assez rapidement on obtient quelques résultats. |  |

Groupe 1
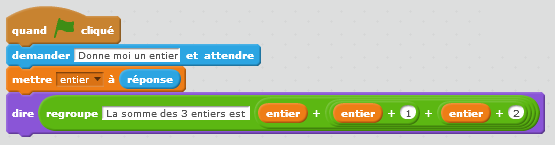
Groupe 2
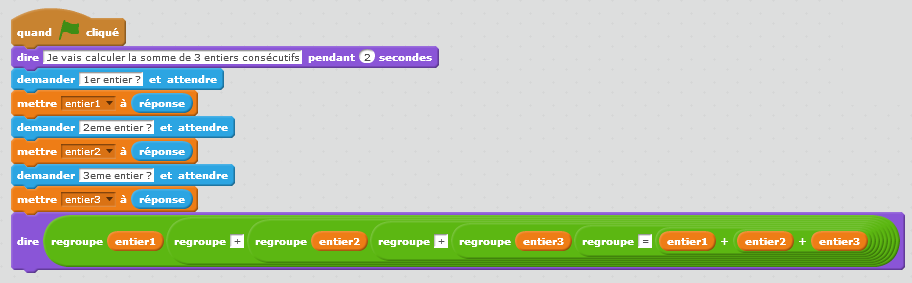
Groupe 3
Le groupe 3 a certainement mieux représenté ses résultats, mais rapidement leur algorithme est mis en défaut lorsqu’on ne rentre pas 3 entiers consécutifs.
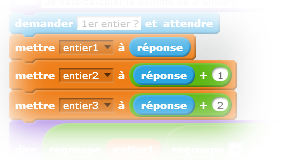
Ils pallient leur problème avec la proposition ci-contre.
L’utilisation de l’instruction « réponse » plusieurs fois de suite pour la même valeur est à déconseiller même si cela fonctionne ici (le problème intervient lorsqu’on programme avec d’autres langages).
La somme de 3 entiers consécutifs est-elle divisible par 3 ?
Cette première partie finie rapidement, je demande de modifier le programme pour tester si la somme obtenue est divisible par 3. Il convient d’introduire une nouvelle instruction auprès des élèves qui calcule le reste de la division euclidienne de 2 entiers (la division euclidienne a été revue en classe).


Deux autres instructions sont expliquées. Ces dernières permettent de faire un test et d’effectuer des instructions différentes selon le résultat de ce test.
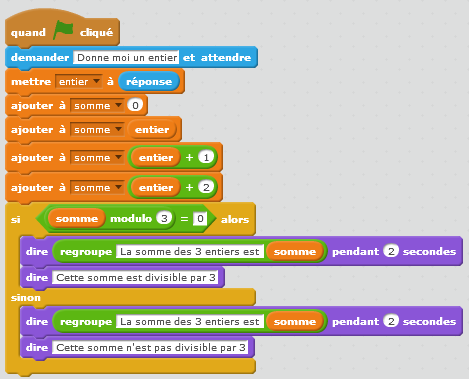
Les élèves sont en mesure maintenant de réaliser la tâche demandée.

La somme de 3 entiers consécutifs est-elle toujours divisible par 3 ?
Problème : une fois le test effectué peut-on dire que cela est toujours vrai. Les élèves se lance dans plusieurs essais et :
« OUI ! Monsieur cela marche toujours ! »
« Est-ce suffisant de faire quelques exemples ? »
« On pourrait tester avec 1 comme nombre de départ, puis avec 2 et ainsi de suite… »
« Sans s’arrêter ? »
« B’en si ! »
« Quand ? »
« … »
« Et 0, comme nombre de départ, on ne le teste pas ? »
« B’en si »
Je teste alors un programme avec comme premier entier 1 milliard de milliards (avant je pose la question aux élèves, « au fait cela s’écrit comment ? » « un 1 suivi de dix-huit 0 », le 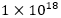
Je demande aux élèves de tester avec leur calculatrice…
Tout le monde n’est pas d’accord (compter des 0 c’est dur), je leur dis donc de taper
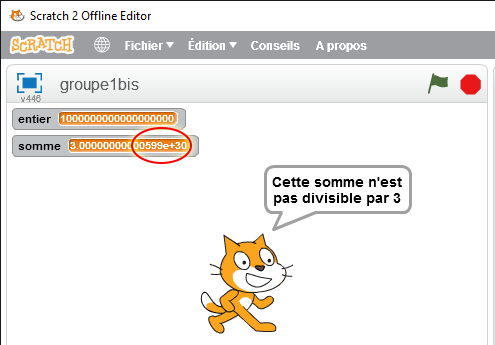
La réponse est, du coup, plus claire pour tout le monde cela fait 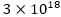
Le « 599 » pose problème aux élèves donc scratch ne sait pas calculer avec des grands nombres. Donc pourquoi lui faire confiance quand elle nous dit que c’est divisible par 3 !
Et pour la calculatrice ? Cela devrait finir par 3, non ? Réponse : « Il n’y a pas assez de place… ».
La conjecture sera donc à prouver lors de la prochaine séance.
La somme de n entiers consécutifs est-elle divisible par n ?
Les consignes sont de modifier le programme pour demander « n », le « 1er entier », puis de calculer la « somme ». L’instruction ci-contre peut s’avérer alors très utile.
Modifications rapides des programmes : « NON ! Monsieur, ça ne marche pas ! J’ai testé pour 4 ! ». Problème le groupe en question n’a pas respectée les consignes… Je leur demande pour n=5, puis 6, puis 7, etc. jusqu’à au moins 30. La remarque étant que cela va être pénible à modifier à chaque fois, ils comprennent finalement l’intérêt de modifier une fois pour toutes le programme.
Groupe 4
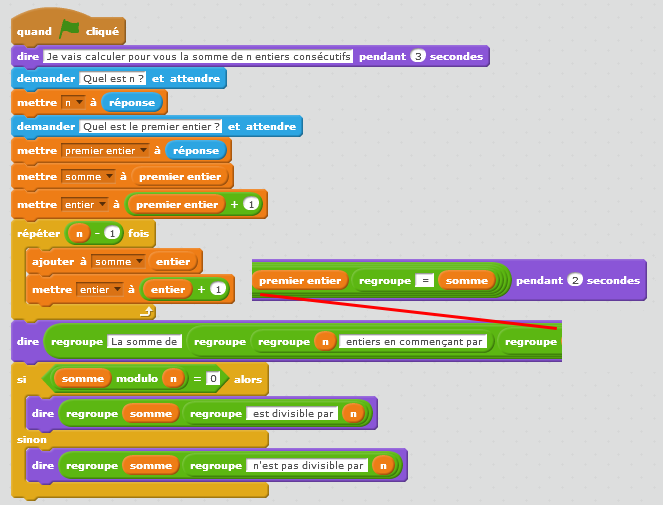
Une conjecture semble émerger de la part des élèves « la somme de n entiers consécutifs semble divisible par n, lorsque n est impair »
Emmanuel malgras, Enseignant au Collège Pierre et Marie Curie - le pellerin (44)
information(s) pédagogique(s)
niveau : tous niveaux, Collèges tous niveaux, 3ème
type pédagogique :
public visé : non précisé, élève, enseignant
contexte d'usage : salle multimedia
référence aux programmes :
documents complémentaires
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA