espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > actions nationales 2007-2009 > Projets de scénarii (lycée)
Aire dans un trapèze
mis à jour le 27/04/2009
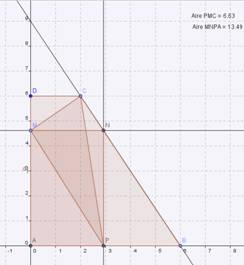
Dans cette figure plane dynamique, on cherche à placer le point M pour avoir deux aires égales : un logiciel de calcul formel est bien apprécié pour transformer l'écriture d'une expression du second degré .
mots clés : aire, équation, calcul formel, factorisation, trapèze
Enoncé de l'activté
L'unité graphique est le cm.
ABCD est un trapèze rectangle de bases [AB] et [CD] tel que :
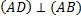 , AB=6, AD= 6 , DC=2.
, AB=6, AD= 6 , DC=2.M est un point mobile sur le côté [AD].
A partir de ce point M, on définit le rectangle AMNP avec N
 [CB] et P
[CB] et P 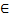 [AB]
[AB] le triangle PMC.
Où placer le point M pour que l'aire du triangle AMNP soit égale à l'aire du triangle PMC ?
Dans un deuxième temps, les élèves souhaitent utiliser un tableur ce qui va les contraindre à passer à l'algèbre : ils vont identifier les variables et mobiliser la notion de fonction. Le tableur ne permet pas de progresser beaucoup dans la conjecture. Il faudrait entreprendre un calcul « à la main » mais les expressions algébriques sont peu engageantes pour un élève de seconde. En effet :
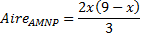 et
et 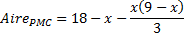 .
.Certains souhaitent écrire l'expression
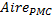 sous forme d'un quotient de dénominateur 3 : le logiciel de calcul formel accompagne le calcul et rassure les élèves. Ils continuent en faisant un produit en croix à la main et obtiennent l'équation :
sous forme d'un quotient de dénominateur 3 : le logiciel de calcul formel accompagne le calcul et rassure les élèves. Ils continuent en faisant un produit en croix à la main et obtiennent l'équation : 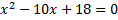 .
.D'autres travaillent avec l'écriture
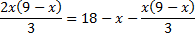 , ils multiplient chaque membre par 3, ajoutent
, ils multiplient chaque membre par 3, ajoutent 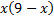 dans chaque membre, puis ajoutent 3x dans chaque membre, ils développent et obtiennent l'équation :
dans chaque membre, puis ajoutent 3x dans chaque membre, ils développent et obtiennent l'équation : 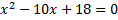 .
. Pour vérifier on peut demander à Xcas le calcul de la différence
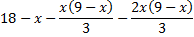 .
.Devant l'équation
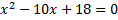 , les élèves souhaitent factoriser mais n'y arrivent pas. Ils vont donc confier cette tâche, un peu délicate pour un élève de seconde, au logiciel de calcul formel.
, les élèves souhaitent factoriser mais n'y arrivent pas. Ils vont donc confier cette tâche, un peu délicate pour un élève de seconde, au logiciel de calcul formel.L'écriture permet d'obtenir
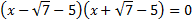 deux solutions dont une seule appartient à [0 ;6].
deux solutions dont une seule appartient à [0 ;6].On peut conclure que la valeur de x cherchée est
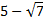 .
.On peut aussi inciter les élèves à demander au logiciel une écriture canonique du polynôme
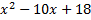 .
. La suite du raisonnement est intéressante à détailler.


Compétences expérimentales
- Prendre l'initiative de construire une figure de géométrie dynamique.
- Prendre l'initiative d'utiliser un tableur (ce qui nécessite d'identifier les variables et les fonctions).
- Prendre l'initiative de mobiliser le calcul formel pour accompagner des calculs compliqués.
- Piloter un logiciel de calcul formel pour obtenir différentes écritures d'une expression algébrique.
information(s) pédagogique(s)
niveau : 2nde
type pédagogique : non précisé
public visé : enseignant, élève
contexte d'usage : non précisé
référence aux programmes :
documents complémentaires
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA


![[legende-image]1239303165725[/legende-image] [legende-image]1239303165725[/legende-image]](https://www.pedagogie.ac-nantes.fr/medias/photo/odt_1449682742019-png)