espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > actions nationales 2007-2009 > Projets de scénarii (lycée)
Autour des identités remarquables
mis à jour le 13/05/2009
Cette activité est une situation à vivre en classe de seconde. Il s'agit de revisiter les identités remarquables en travaillant sur les quantificateurs et les différents sens du signe =. Le calcul formel, inutile pour la première question, pourra être mobilisé pour la suite.
mots clés : identité remarquable, égalité, équation, calcul formel, développer, factoriser
Enoncé de l'activité
Le plan est rapporté à un repère
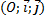 .
.Déterminer et représenter l'ensemble des points
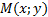
 tels que :
tels que : a)

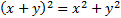
b)

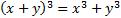
Question Défi pour stimuler les élèves les plus rapides.
Déterminer et représenter l'ensemble des points
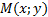
 tels que :
tels que : 
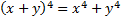
Objectif
Cette activité est une situation intéressante à faire vivre en classe de seconde.
Il s'agit de revisiter les identités remarquables en travaillant sur les quantifications (souvent implicites) et les différents sens du symbole = qui sont liés par ces
 quantifications.
quantifications. L'élève ne s'approprie bien l'énoncé qu'après avoir réfléchi à des phrases du type :
« quels que soient les réels a et b ,
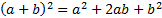
 »
»« il existe des réels a et b tels que
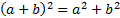 »
»« rechercher tous les réels a et b tels que
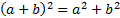
 »
»Déroulement du scénario
Dans un premier temps, les élèves sont choqués que l'on puisse écrire
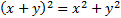 , c'est le début d'une discussion sur les différents sens du symbole = en liaison avec les quantificateurs.
, c'est le début d'une discussion sur les différents sens du symbole = en liaison avec les quantificateurs.Une élève fait observer à ses camarades que, si l'égalité est fausse en général, elle peut être vraie pour certaines valeurs de x et de y : elle propose x = 0 et y = 0.
Un élève propose de travailler sur l'équation
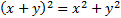 .
.Plusieurs élèves arrivent à l'équation 2xy = 0 puis le lien avec le produit nul est fait : mais il y a hésitation entre « x = 0 et y = 0 » et « x = 0 ou y = 0 ».
La représentation géométrique des points solutions se fait relativement sans problème et permet de (re)parler de la notion d'équation de droite.
A partir du b), on peut s'affranchir des difficultés de calcul en utilisant un logiciel de calcul formel ( par exemple Xcas ou Wiris).
Le calcul formel ne dispense aucunement l'élève de l'élaboration d'une stratégie. La transformation de la question posée en une autre question que l'on peut traiter reste à sa charge. Par exemple, traduire le problème en « rechercher tous les réels a et b tels que
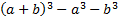 . L'intelligence des calculs des calculs à faire pour traiter cette question reste également à sa charge : développer, factoriser ?
. L'intelligence des calculs des calculs à faire pour traiter cette question reste également à sa charge : développer, factoriser ?Le calcul formel, inutile pour la première question, pourra aider certains élèves pour mener à bien les calculs du b) .
Il ne dispense que de la maîtrise technique quand la maîtrise du cas simple est avérée.

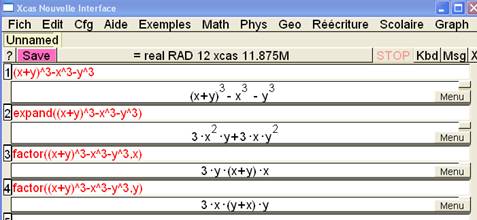
Il devient précieux pour les élèves qui abordent la question défi.


On produit différentes écritures d'une expression par développement ou factorisation. La résolution d'une équation poussera à opter pour la forme factorisée.
Dans le défi, l'écriture de
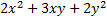 sous la forme canonique
sous la forme canonique 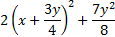 est intéressante à exploiter et donne lieu à une véritable réflexion sur les informations apportées par cette nouvelle écriture (une somme de deux carrés est nulle ssi les deux termes sont nuls...).
est intéressante à exploiter et donne lieu à une véritable réflexion sur les informations apportées par cette nouvelle écriture (une somme de deux carrés est nulle ssi les deux termes sont nuls...).Un élève a même obtenu
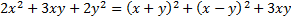 : joli mais pas très intéressant ici.
: joli mais pas très intéressant ici.Compétences mathématiques
- Revisiter les identités remarquables.
- Travailler sur le concept égalité/équation en liaison avec les quantifications.
- Modifier l'écriture d'une expression algébrique et choisir la forme la plus adéquate pour résoudre un problème donné.
- S'entraîner au raisonnement et à la logique : sens des mots ET et OU, CONTRE-EXEMPLE.
Compétences expérimentales ( pour le b) ou la question défi )
- Prendre l'initiative de déléguer à un logiciel de calcul formel une tâche calculatoire dont on connaît la nature mais dont on ne maîtrise pas la technicité.
- Piloter un logiciel de calcul formel après avoir identifié un besoin de calcul ou une stratégie à suivre.
information(s) pédagogique(s)
niveau : 2nde
type pédagogique : non précisé
public visé : enseignant, élève
contexte d'usage : non précisé
référence aux programmes :
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA

