mathématiques

On considère un triangle équilatéral ABC . On place sur un de ses côtés un point mobile M. On définit les points P et Q comme projetés orthogonaux de M sur chacun des deux autres côtés.

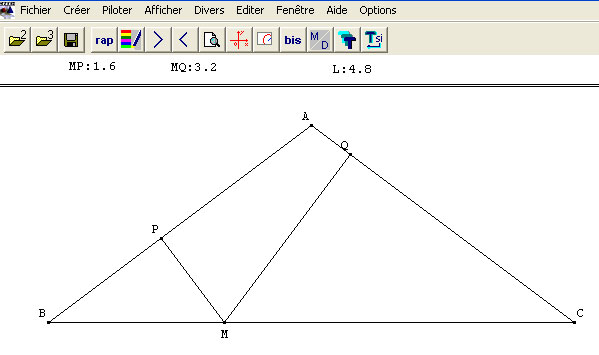
1. a)Réaliser à l'aide d'un logiciel de géométrie dynamique la figure respectant les contraintes ci-dessus.
   b)Afficher la longueur L = MP+MQ
   c)Émettre une conjecture quant à la longueur L.
2. Démontrer la conjecture émise.

Reprendre les questions précédentes dans le cas où ABC est un triangle isocèle le point M étant mobile sur l'un des côtés.

Tout d'abord, il est à noter que les élèves ne rencontrent pas de difficulté majeure de compréhension de l'énoncé. La notion de projeté orthogonal ne pose pas de problème.
Pour certains, les premières difficultés arrivent pour construire un triangle équilatéral, le logiciel utilisé demandant une réflexion préalable pour réaliser cette construction.
Les explications étant données, les élèves gèrent pour une très grande majorité avec succès le statut de « point libre » de M. Finalement, la figure dynamique est obtenue assez facilement (on peut penser que par habitude d'utilisation, les problèmes rencontrés pour construire les triangles n'apparaîtront plus dans d'autres exercices du même type)

La création des longueurs MP et MQ puis l'affichage de la longueur somme L ne pose pas de problème majeur, on peut bien sûr aider un élève ne se rappelant plus du menu concerné pour l'affichage, cela n'a rien de pénalisant.
Les élèves utilisent bien sûr le côté dynamique du point M pour émettre la conjecture : la longueur L est constante.

Cette activité se prête bien au découpage 3/4 - 1/4 tel qu'on peut le rencontrer dans les exercices proposés en terminale pour l'épreuve expérimentale.
En effet, la partie « construction de la figure + conjecture » réalisée précédemment prend entre 30 et 40 minutes au élèves, le temps restant étant consacré à la démonstration de cette conjecture.
Très peu (pour ne pas dire aucun) d'élèves savent comment « démarrer » cette démonstration : la première aide proposée peut consister juste à dire à l'élève de tracer le segment [AM] lui permettant de visualiser le découpage du triangle ABC en deux triangles AMP et AMQ.
Après un temps de réflexion, on peut indiquer à l'élève le recours aux calculs d'aires de triangles...pour la suite, c'est la qualité des calculs menés qui fait la différence.
Une mise au point s'impose au cours suivant mais tous les élèves auront été en réelle activité mathématique.

Elle demandera un réinvestissement de la partie A avec une analyse critique et une discussion suivant le côté sur lequel M est mobile.