espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > actions nationales 2007-2009 > Projets de scénarii (lycée)
Promenade sur un triangle
mis à jour le 15/05/2008
Une situation géométrique simple qui conduit à la notion de fonction. La représentation graphique est étonnante et mérite d'être exploitée à l'oral.
mots clés : Tice, fonction, conjecture, initiative, géométrie dynamique
Enoncé de l'activité
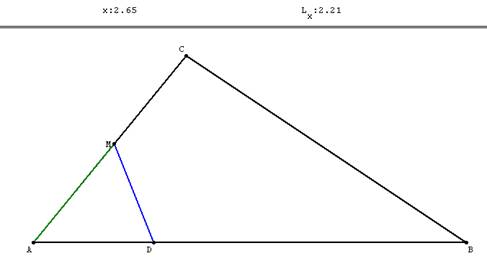
ABC est un triangle tel que AC = 5, CB = 7 et AB = 9, l'unité de mesure de longueur est le kilomètre. Sur le coté [AB] se trouve le point D à 2,5 km de A.
Un point M se déplace sur le triangle, il décrit le trajet ACB. On note x la longueur du trajet effectué par M et L(x) la longueur MD.
Conjecturer les variations de la fonction L
On peut utiliser le logiciel Géoplan:
Réaliser deux figures :la première lorsque M se déplace de A vers C, la deuxième lorsque M dépasse C et continue son trajet jusqu'à B, faire afficher les valeurs x et L(x).
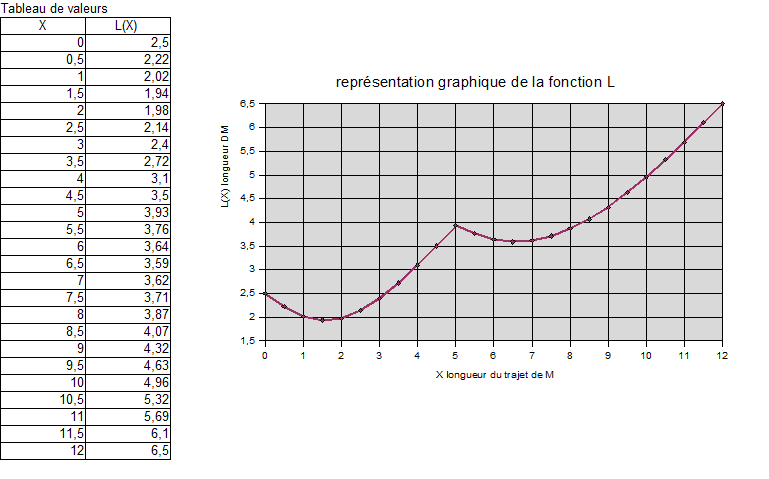
On peut utiliser ensuite en parallèle le tableur open office .calc
Remplir un tableau de valeurs de la fonction L et créer la représentation graphique correspondante.
Objectifs
Approcher la notion de fonction par un grand nombre de valeurs et un graphique grâce aux TICE
Découvrir une fonction non monotone sur un intervalle et la notion de distance d'un point à une droite
S'approprier le logiciel Géoplan pour la création d'un point libre sur un segment, son pilotage, la création et l'affichage de numériques.
Réaliser un graphique avec un tableur.
Découvrir une fonction non monotone sur un intervalle et la notion de distance d'un point à une droite
S'approprier le logiciel Géoplan pour la création d'un point libre sur un segment, son pilotage, la création et l'affichage de numériques.
Réaliser un graphique avec un tableur.
Réalisation avec Géoplan
Les compétences expérimentales développées
- Utiliser les outils de construction d'un logiciel de géométrie dynamique.
- Placer et piloter un point libre sur un segment.
- Prendre l'initiative d'utiliser un tableur pour organiser et traiter des données.
- Enoncer une conjecture claire (concernant le sens de variation de la fonction par observation des comportements respectifs des numériques).
- Prendre l'initiative de créer un graphique à partir d'un tableau de données.
- Repérer une figure clé dans une situation plus complexe (ici distance d'un point à une droite)
- Enoncer une conjecture claire (concernant les positions de M correspondants aux minimums de la fonction)
- Tester des cas particuliers.
information(s) pédagogique(s)
niveau : 2nde
type pédagogique : non précisé
public visé : enseignant, élève
contexte d'usage : non précisé
référence aux programmes :
documents complémentaires
| Les fichiers associés |
La version ODT  de cette activité. de cette activité. |
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA