mathématiques

espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > actions nationales 2007-2009 > Projets de scénarii (lycée)

Tangente à un cercle

mis à jour le 28/05/2008

Un lieu étonnant à découvrir par la géométrie dynamique.Activité à prolonger par un devoir maison.

mots clés : Tice, tangente à un cercle, médiatrice, produit scalaire, trace, lieu, triangles semblables

Enoncé de l'activité

(C) est un cercle de centre O et de rayon 3, H est un point du plan tel que OH = 5. On note (d) la perpendiculaire à (OH) passant par H.
M est un point quelconque de (d). On construit les droites issues de M tangentes au cercle (C) en B et C. La droite (BC) coupe (OH) en I et (OM) en N.
Le but de cette activité est de déterminer le lieu du point N lorsque le point M décrit la droite (d).

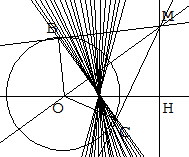
Créer une figure dynamique permettant d'observer le lieu du point N.
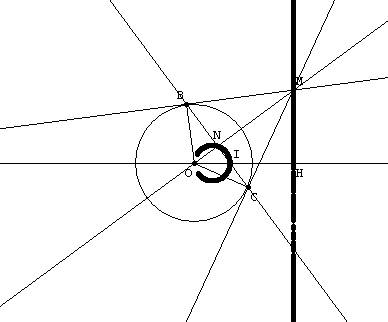
La droite (BC) semble passer par un point fixe. Lequel ? Emettre une conjecture concernant le lieu du point N
Prouver la conjecture précédente.

Objectifs

Découvrir l'existence d'un point fixe et la nature d'un ensemble de points à l'aide d'un logiciel de géométrie dynamique.
Réactiver la connaissance de la configuration de tangentes à un cercle.
Utiliser l'outil produit scalaire pour la démonstration

Prolongements possibles

Dans le cadre d'une gestion de classe hétérogène, on peut proposer à des élèves de regarder ce qui se passe quand H est sur le cercle (OH=3) ou à l'intérieur (OH< 3).
Demander aux élèves de rédiger la preuve en devoir maison en fournissant éventuellement un questionnement.

Quelques vues attendues

Réalisation avec Géoplan :

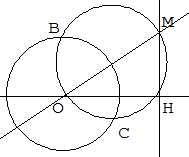
Les compétences expérimentales pouvant être évaluées

Placer un point libre sur un objet, le piloter.
Elaborer une démarche : construction des tangentes au cercle issues de M.
Prendre l'initiative de visualiser la trace d'une droite ou d'un point.
Enoncer clairement une conjecture.
Prendre l'initiative de tester des positions limites et d'observer des cas particuliers.
Découvrir des invariants d'une figure et les exploiter .