espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > actions nationales 2007-2009 > Projets de scénarii (lycée)
Triangles sous hyperbole
mis à jour le 28/05/2008
Cette situation facile d'accès et bien illustrée par les TICE permet de réactiver les connaissances d'analyse de 1S et de mettre en place une différenciation pédagogique.
mots clés : Tice, fonction, conjecture, initiative, tangente, limite
Enoncé l'activité
On considère la fonction f définie sur ] 0 ;
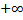 [ par
[ par 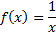 .
.On appelle (Cf) la courbe représentative de f dans un repère orthonormé
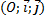 d'unité 1 cm.
d'unité 1 cm.La tangente en un point quelconque de la courbe (Cf) coupe l'axe des abscisses en M et l'axe des ordonnées en N.
Comment varie l'aire du triangle OMN ? ( ou Etudier l'aire du triangle OMN).
Objectifs
L'objectif est de découvrir que l'aire du triangle OMN semble constante et de prouver ce résultat.
Mais les rebondissements dans le scénario nous ont amenés à travailler aussi avec les fonctions g et h définies sur ] 0 ;
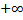 [ par
[ par 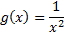 et
et 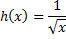 .
.Les révisions sur les limites et les formes indéterminées ont été intéressantes.
Scénario
Cette recherche nécessite un logiciel de géométrie dynamique capable aussi de tracer des courbes, des tangentes et d'évaluer l'aire d'un triangle (par exemple Géogébra, Géoplan ou TInspire). A noter que le choix du logiciel a son importance : le tracé d'une tangente par exemple ne se fera pas de la même façon avec Géogébra et avec Géoplan.
1. Ce qui a été fait avant
L'énoncé a été donné en devoir à faire à la maison. En fait, les élèves ont cherché quelques jours autour de cet énoncé, puis nous avons fait une séance de travail dirigé pour avancer dans le problème. Il a fallu une deuxième séance de travaux dirigés pour répondre à toutes les questions posées. La preuve du résultat a été rédigée sur copie.
2. Le déroulement
J'ai utilisé pour ces séances la calculatrice TInspire.
Première animation
On commence par construire une première animation : un point libre A est placé sur la courbe représentant la fonction inverse sur ] 0 ;
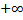 [, la tangente en A est tracée et le triangle AMN est visualisé par un remplissage en gris. Au début, la réflexion des élèves est la suivante « au départ le triangle est plutôt plat donc il a une aire presque nulle, puis il se remplit et enfin il redevient plat . Il doit donc y avoir un endroit où l'aire de ce triangle est maximale. Il reste à chercher à quel endroit se produit ce maximum ».
[, la tangente en A est tracée et le triangle AMN est visualisé par un remplissage en gris. Au début, la réflexion des élèves est la suivante « au départ le triangle est plutôt plat donc il a une aire presque nulle, puis il se remplit et enfin il redevient plat . Il doit donc y avoir un endroit où l'aire de ce triangle est maximale. Il reste à chercher à quel endroit se produit ce maximum ».Deuxième animation
On complète le travail précédent en faisant afficher l'aire du triangle.
Maintenant, on peut lire l'aire du triangle au fur et à mesure que le point A se déplace sur la courbe.
Ici la conclusion des élèves est : « la calculatrice ne marche pas : la valeur de l'aire est bloquée à 2 »
Pour lever le doute, je propose de changer la fonction f et de traiter le même problème en changeant la fonction f.
Avec la fonction g définie sur ] 0 ;
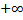 [ par
[ par 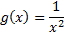 ,on peut rassembler les quelques remarques suivantes formulées naïvement :
,on peut rassembler les quelques remarques suivantes formulées naïvement : Avec cette nouvelle fonction g, on constate que l'aire du triangle OMN est bien variable .
Dans ce cas, l'aire semble décroissante.
Si l'abscisse du point A est proche de zéro, l'aire est grande pourtant le triangle a l'air « plat ».
Avec la fonction h définie sur ] 0 ;
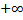 [ par
[ par 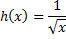 , les réflexions sont les suivantes :
, les réflexions sont les suivantes :Avec cette nouvelle fonction h, on constate que l'aire du triangle OMN est bien variable .
Dans ce cas, l'aire semble croissante.
Si l'abscisse du point A est très grande, l'aire est grande pourtant le triangle a l'air « plat ».
Enfin la conjecture liée au problème posé.
Pour revenir à notre problème de départ avec la fonction f définie sur ] 0 ;
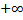 [ par
[ par 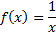 , on peut conjecturer l'idée suivante : l'aire du triangle OMN semble constante et égale à 2.
, on peut conjecturer l'idée suivante : l'aire du triangle OMN semble constante et égale à 2.Cette conjecture sera démontrée dans le devoir maison.
Deux nouvelles conjectures.
Les démonstrations peuvent être demandées à certains élèves dans le cadre d'une différenciation pédagogique.
| Conjecture 1 | Conjecture 2 |
La fonction g définie sur ] 0 ; 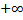 [ par [ par 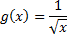 . .La tangente en un point A quelconque de la courbe (Cg) coupe l'axe des abscisses en M et l'axe des ordonnées en N. On dirait que l'aire du triangle OMN est croissante. Le prouver. Que devient l'aire du triangle OMN quand l'abscisse de A tend vers 0 ? quand l'abscisse de A tend vers l'infini ? | La fonction h définie sur ] 0 ; 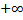 [ par [ par 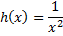 . .La tangente en un point A quelconque de la courbe (Ch) coupe l'axe des abscisses en M et l'axe des ordonnées en N. On dirait que l'aire du triangle OMN est décroissante. Le prouver. Que devient l'aire du triangle OMN quand l'abscisse de A tend vers 0 ? quand l'abscisse de A tend vers l'infini ? |
Compétences expérimentales à évaluer
- Illustrer, représenter une situation avec un logiciel
- Placer un point libre sur un objet .
- Enoncer clairement une conjecture.
- Prendre l'initiative d'explorer des conditions limites.
- Tester la robustesse d'une conjecture.
- Prendre l'initiative de faire une analyse critique d'un résultat.
information(s) pédagogique(s)
niveau : 1ère S, Terminale S
type pédagogique : non précisé
public visé : enseignant, élève
contexte d'usage : non précisé
référence aux programmes :
documents complémentaires
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA



