espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > actions nationales 2007-2009 > Projets de scénarii (lycée)
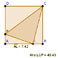
Un triangle dans un carré
mis à jour le 28/05/2008
Une activité classique en seconde qui fait intervenir une fonction issue d'une situation géométrique. Possibilité de mobiliser le calcul formel.
mots clés : Tice, fonction, conjecture, initiative, géométrie dynamique
Enoncé de l'activité
On considère un carré ABCD de côté 10 cm. Sur le côté [AB], on place un point L mobile.
On place sur le côté [DA] un point P tel que AL=DP. On construit alors le triangle LCP.
Le but de l'exercice est de déterminer s'il existe un triangle LCP d'aire minimale.
- Réaliser à l'aide d'un logiciel de géométrie dynamique la figure répondant aux contraintes de l'énoncé.
- Afficher la longueur AL ainsi que l'aire du triangle LCP.
- Émettre une conjecture quant à l'aire minimale du triangle LCP.
- Démontrer la conjecture émise.
Objectifs poursuivis
Cette activité s'adresse à des élèves de seconde et permet d'illustrer le cours sur les fonctions par un exemple issu d'une situation géométrique simple.
Elle peut servir d'introduction à la notion de fonction car les calculs à faire pour déterminer l'aire du triangle LCP sont très abordables dès le début de l'année; elle peut aussi être prolongée plus tard dans la progression du cours sur les fonctions pour illustrer la notion de minimum d'une fonction. On peut aussi s'en servir en fin de parcours en y ajoutant la compréhension de la notion de variations d'une fonction sur un intervalle.
Les élèves ont aussi à gérer la qualité « mobile » du point L sur le segment [AB] ce qui leur permettra ensuite d'émettre des conjectures sur l'aire du triangle LCP.
Stratégies suivies par les élèves
Cette activité a été traitée en classe avec le logiciel Géoplanw
Construction de la figure
Le début de la construction ne pose aucun problème aux élèves qui très rapidement mettent en place le carré ABCD et le point mobile L sur le segment [AB].
Avec le logiciel mis en pratique, les élèves ont du mal à créer le point P tel que AL=DP. Il faut donc prendre du temps pour d'une part les laisser chercher pour mettre en oeuvre une stratégie possible avec les menus du logiciel, d'autre part mettre en commun une méthode adéquate pour placer ce point P. C'est une difficulté à laquelle on ne s'attend pas mais qui bloque beaucoup d'élèves ... elle est facile à mettre en évidence en demandant à l'élève qui pense avoir fini sa construction de « bouger » le point L, il s'aperçoit alors que le point P n'est pas mobile et que la contrainte AL=DP n'est pas respectée.
Avec le logiciel mis en pratique, les élèves ont du mal à créer le point P tel que AL=DP. Il faut donc prendre du temps pour d'une part les laisser chercher pour mettre en oeuvre une stratégie possible avec les menus du logiciel, d'autre part mettre en commun une méthode adéquate pour placer ce point P. C'est une difficulté à laquelle on ne s'attend pas mais qui bloque beaucoup d'élèves ... elle est facile à mettre en évidence en demandant à l'élève qui pense avoir fini sa construction de « bouger » le point L, il s'aperçoit alors que le point P n'est pas mobile et que la contrainte AL=DP n'est pas respectée.
Conjecture émise
La figure étant validée, la création de la longueur AL est aisée ainsi que celle de l'aire du triangle LCP puisque le logiciel utilisé prévoit des menus directement « utilisables ». Il reste à utiliser la qualité dynamique de la construction du point L pour émettre une conjecture quant à l'aire minimale du triangle LCP.
Démonstration
Cette activité très classique se prête bien au découpage 3/4 - 1/4 tel qu'on peut le rencontrer dans les exercices proposés en terminale pour l'épreuve expérimentale.
En effet, la partie « construction de la figure + conjecture » réalisée précédemment prend entre 30 et 40 minutes au élèves, le temps restant étant consacré à la démonstration de cette conjecture.
Il est évident que le caractère « ouvert » de la question laisse beaucoup (trop ?) d'initiatives à l'élève : mettre en place la variable (poser x=AL paraît naturel pour beaucoup mais pas pour tous), cette variable étant posée, calculer l'aire du triangle LCP demande réflexion et des calculs (Géoplanw donne l'aire directement, l'élève doit procéder par différence entre l'aire du carré et l'aire de trois triangles).La « fonction aire » étant déterminée, la comparer à l'aire minimale conjecturée dans la partie précédente n'est pas facile et demande beaucoup d'autonomie et une compréhension assez poussée de la notion d'extremum.
En effet, la partie « construction de la figure + conjecture » réalisée précédemment prend entre 30 et 40 minutes au élèves, le temps restant étant consacré à la démonstration de cette conjecture.
Il est évident que le caractère « ouvert » de la question laisse beaucoup (trop ?) d'initiatives à l'élève : mettre en place la variable (poser x=AL paraît naturel pour beaucoup mais pas pour tous), cette variable étant posée, calculer l'aire du triangle LCP demande réflexion et des calculs (Géoplanw donne l'aire directement, l'élève doit procéder par différence entre l'aire du carré et l'aire de trois triangles).La « fonction aire » étant déterminée, la comparer à l'aire minimale conjecturée dans la partie précédente n'est pas facile et demande beaucoup d'autonomie et une compréhension assez poussée de la notion d'extremum.
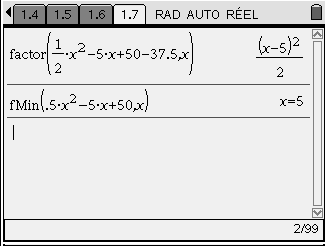
Il est possible de recourir (au moins pour certains élèves) à un logiciel de calcul formel qui donnera une réponse que chacun pourra vérifier. En effet la fonction donnant l'aire du triangle LCP est A(x)=0,5x²-5x+50. Comme on a pu conjecturer un minimum quand x=5,la preuve consiste à montrer que A(x)-A(35)est un nombre positif. Le logiciel de calcul formel peut ici apporter une aide intéressante.
Tice : intérêts de l'outil
Le logiciel utilisé permet de rendre dynamique la figure, les élèves peuvent donc tout naturellement faire « bouger » le point L sur le segment [AB].
L'outil TICE prend donc ici toute son importance puisqu'il permet de mettre en évidence une propriété qui peut paraître évidente pour certains mais qui, illustrée dynamiquement par le logiciel, prend du sens pour tous.
Remarque :
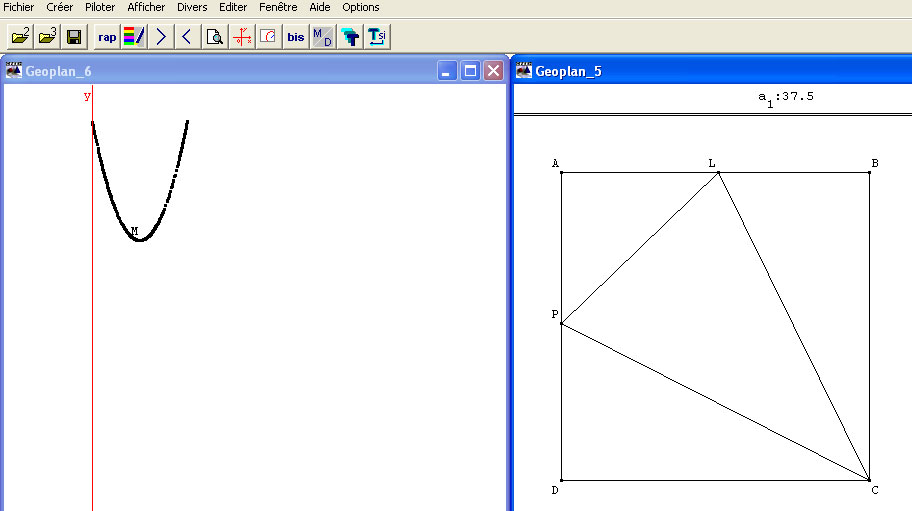
Les élèves peuvent aussi travailler sur deux fenêtres pour faire le lien entre la situation géométrique et la courbe de la fonction mise en oeuvre.
Ce n'est peut-être pas une compétence à acquérir systématiquement mais les élèves, une fois familiarisés avec les menus correspondants (piloter, importer) se sentent de plus en plus à l'aise.
Compétences expérimentales évaluées
- Traiter l'information (l'élève s'approprie l'énoncé pour le « traduire » avec l'outil TICE)
- Émettre clairement une conjecture (l'outil TICE au service des mathématiques)
- Prendre l'initiative de faire une analyse critique de la production (réflexion de l'élève par rapport au support informatique utilisé et au résultat conjecturé)
- Prendre l'initiative de mobiliser un logiciel de calcul formel pour certains calculs plus complexes.
information(s) pédagogique(s)
niveau : 2nde
type pédagogique : non précisé
public visé : enseignant, élève
contexte d'usage : non précisé
référence aux programmes :
documents complémentaires
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA