mathématiques

espace pédagogique > disciplines du second degré > mathématiques > enseignement > actions nationales > actions nationales 2011-2012

la pyramide

mis à jour le 29/04/2012

Cette activité permet au élève de s'approprier la modélisation du problème rapidement identifié comme une situation nécessitant des suites.

mots clés : TraAM, modélisation, suite, suite arithmétique, calcul formel, tableur

Compétence calculatoire travaillée ou en lien avec ces activités

Modéliser une situation à l'aide des suites.
Mise en œuvre de la formule 1+2+...+n
Mobilisation des acquis sur les suites arithmétiques.
Faire le lien entre différentes écritures algébriques d'un nombre obtenues par différentes stratégies.
Possibilité de mise en œuvre d'une démarche de vérification grâce à un logiciel de calcul formel.

Descriptif rapide

Les élèves utilisent différentes stratégies pour découper la pyramide et obtiennent différentes écritures pour le nombre de cubes qui composent une pyramide à n étages. L'interaction entre la vision géométrique et les calculs est fructueuse : les calculs ont du sens, le passage à l'algèbre permet une généralisation.

Travail de recherche donné en 1S en novembre deux semaines après le début de la séquence sur les suites.
Remarque : Dans la pratique de la classe est installée l'habitude de proposer des problèmes ouverts qui ne mobilisent pas nécessairement les outils mathématiques étudiés dans la séquence travaillée

Enoncé donné aux élèves

Voici un empilement de cubes à 5 niveaux

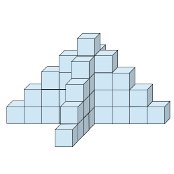
Combien y a-t-il de cubes dans cet empilement à 5 niveaux ?
Combien y a-t-il de cubes dans un empilements à n niveaux ?
Quel est le plus grand empilement de ce type que l'on peut réaliser si on dispose de 12420 cubes ?

Remarque : on aurait pu limiter l'énoncé du problème à la seule question 3.

Objectifs

Mettre en œuvre une recherche de façon autonome, mener des raisonnements, avoir une attitude critique vis-à-vis des résultats, choisir et appliquer des techniques de calcul, modéliser et étudier une situation à l'aide des suites.

Cette activité posée sous forme ouverte vise prioritairement à renforcer la maitrise des compétences de résolution de problème. Elle permet de donner sens à la notion de suite et d'utiliser les formules de sommation.

Vous pouvez accéder au scénario complet ci-dessous...

auteur(s) :

Gérard CORDES, enseignant au lycée Jean De Lattre de Tassigny (La Roche sur Yon)

information(s) pédagogique(s)

niveau : 1ère S

type pédagogique : non précisé

public visé : enseignant, élève

contexte d'usage : classe, salle multimedia, atelier

référence aux programmes :

documents complémentaires

le scénario complet

le scénario complet

haut de page

mathématiques - Rectorat de l'Académie de Nantes