espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > actions nationales 2013-2015
accidents mortel : baisse de 50% ?
mis à jour le 04/05/2015
Peut-on envisager une baisse de 50 % du nombre d’accidents mortels sur les routes belges par rapport à l’année 2000 ?
mots clés : traam, vidéo, statistiques à 2 variables, ajustement affine
Descriptif
Problématique
Une vidéo d’environ une minute est présentée aux élèves, une première fois en totalité :
| Code à insérer dans le code source d'une page HTML5 (elyco) |
| <p style="text-align: center;"><video width="480" height="360" controls="controls"> <source src="http://www.pedagogie.ac-nantes.fr/html/peda/math/Video/TraAM/2014-15/Accidents.mp4" type="video/mp4"></source> </video> </p> |
Cette vidéo est extraite d’un reportage lors d’un journal télévisé sur la chaine belge RTBF.
Elle évoque l’évolution du nombre d’accidents mortels sur les routes belges depuis l’année 2000. Ce nombre qui avait tendance à baisser depuis 11 ans est reparti à la hausse depuis l’année 2011.
De cet extrait, on dégage la problématique suivante :
Peut-on envisager une baisse de 50 % du nombre d’accidents mortels sur les routes belges par rapport à l’année 2000 ?

Mise en œuvre
Les élèves sont donc sensés connaitre l’utilisation de la calculatrice ou du tableur afin de réaliser un ajustement affine et ainsi faire des prévisions.
Temps 1 : (10 minutes) – Deux diffusions de la vidéo en totalité et une problématique
« Peut-on envisager une baisse de 50 % du nombre d’accidents mortels sur les routes belges par rapport à l’année 2000 ? »
Temps 2 : (30 minutes) – Un temps de recherche en binôme
Tous les groupes ont l’idée de construire un tableau statistique en reprenant les données du graphique. Dans ce tableau, apparaissent « l’année » et « le nombre de décès ».
La difficulté réside dans le fait que l’écart entre les différentes années varie. En effet, si l’on attribue le rang 1 à l’année 2000, il faut donner le rang 6 à l’année 2005, et ainsi de suite.
Une fois le tableau à 2 variables statistiques « Rang de l’année » et « Nombre de décès » correctement construit, les élèves n’ont aucune difficulté à saisir ces données sur leur calculatrice, et ainsi obtenir un ajustement affine.
Le calcul du pourcentage ne pose pas de problème particulier.
La dernière étape consiste en la résolution d’une équation du 1er degré ; ce dernier point est généralement bien maitrisé par les élèves.
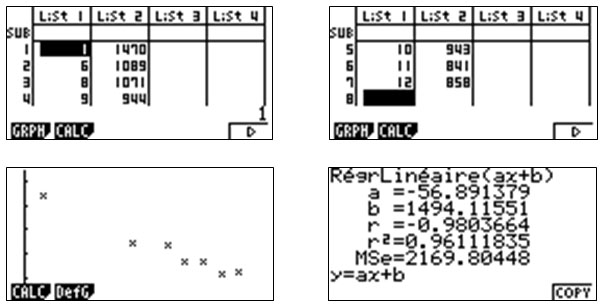
Voici le travail réalisée par un binôme ; les différents copies d’écran montrent le tableau statistique, le nuage de points ainsi que l’ajustement affine réalisé (coefficients a et b).
L’équation de droite obtenue est :
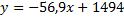
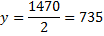
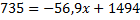
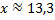
Au cours de l’année 2012, il est raisonnable d’envisager un nombre de décès sur les routes belges égal à la moitié de celui de l’année 2000.
L’étude des probabilités a été réalisée par la suite.
Olivier Charruau, Enseignant au lycée Professionnel Branly à La Roche sur Yon (85)
information(s) pédagogique(s)
niveau : tous niveaux, Lycée professionnel tous niveaux, 2nde professionnelle, Lycée tous niveaux, 2nde
type pédagogique :
public visé : non précisé, élève, enseignant
contexte d'usage : travail autonome
référence aux programmes :
documents complémentaires
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA


