espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > actions nationales 2013-2015
éclipse de cube
mis à jour le 12/05/2015
L'objectif de cette activité est de calculer l'aire de l'ombre au sol d'une maison cubique éclairée par un lampadaire.
mots clés : traam, vidéo, géométrie dans l'espace, 3D, réalité augmentée
Description
L'objectif de cette activité est de calculer l'aire de l'ombre au sol d'une maison cubique éclairée par un lampadaire. Lors de la séance les élèves devaient dessiner la figure complète sur une feuille de papier avec une règle et un crayon puis ils devaient calculer l'aire de cette ombre. Pour les aider, la figure du problème puis sa solution ont été projetées sur un tableau numérique interactif en réalité augmentée grâce à un téléphone portable. Les élèves pouvaient ainsi se déplacer autour de la figure virtuelle et appréhender un peu mieux la situation.
| Code à insérer dans le code source d'une page HTML5 (elyco) |
| <p style="text-align: center;"><video width="480" height="360" controls="controls"> <source src="http://www.pedagogie.ac-nantes.fr/html/peda/math/Video/TraAM/2014-15/Projet d une maison cubique a etage.mp4" type="video/mp4"></source> </video> </p> |
Dans une classe de seconde, au début d'une séance en classe entière, une vidéo d'1 min 30 sans parole a été présentée pour introduire le problème et l'ancrer dans la réalité.
| Dans cette vidéo, on tourne autour d'une maison dessinée en image de synthèse. Lors de la première projection, les élèves se sont mis à réagir et à dialoguer. Ils ont été particulièrement frappés par Dans une rue, un lampadaire vertical éclaire une maison cubique. La maison est représentée ci-contre par le cube ABCDEFGH. La distance AB=4 m. Le lampadaire qui mesure 8 m se trouve sur la demi-droite [CD) à 4 m du point D. Calculer l'aire de l'ombre de cette maison au sol. | 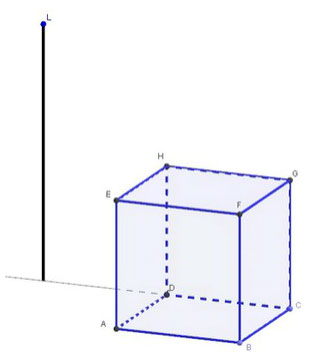 |
Le texte a été distribué sous forme papier avec la consigne de faire l'activité à la maison pour le lendemain.
Après une courte parenthèse historique, sans donner plus de détails, nous sommes passés à tout autre chose.
Mise en œuvre
Ce qui a été fait avant
En début d'année deux séances d'une heure ont été faites en salle informatique sur le logiciel Interesp (exerciseur permettant de travailler sur les positions relatives de droites et de plans). Puis, régulièrement, les élèves ont eu d'une part des exercices du même type à faire avec papier-crayon et, d'autre part des activités à chercher dans lesquels apparaissaient des configurations conduisant à des problèmes aptes à mobiliser d’autres champs des mathématiques (volume maximal d'une boite, aire de la section d'un cube...).
Au cours de l'année, le théorème de Thalès dans des configurations planes et le « Théorème du toit » ont été utilisés plusieurs fois par les élèves.
Déroulement de la séquence
Temps 1 : Diffusion d'une vidéo en classe entière pour introduire la problématique, puis présentation du problème (5 minutes)
En début de séance, en classe entière, la vidéo sans parole de 90 secondes a été présentée à la classe pour introduire le problème et l'ancrer dans la réalité (lien sur la vidéo). Dans cette vidéo, on tourne autour d'une maison dessinée en images de synthèse. Lors de la première projection, les élèves se sont mis à réagir et à dialoguer. J'ai pu entendre entre autre : «qu'est ce qu'elle est belle ! », « c'est trop bien fait !», « on dirait une vraie !»...
A ce moment là, j'ai pris la parole pour dire : « Oui, c'est vrai. Mais pourquoi on dirait une vraie ? »
Réponse d'un élève : «Parce qu'on voit même les reflets dans les vitres »,
Réponse d'un autre : « Parce qu'il y a les nuages »
Réponse d'un troisième : « Parce qu'il y a l'ombre »
J'ai alors repassé la vidéo en remontrant les différentes ombres : celles des murs de la rampe descendant au sous-sol, celles du balcon, celles du feuillage, celles de la balançoire … en leur faisant remarquer que cela ne devait pas être évident à dessiner. J'ai poursuivi en disant que nous n'allions pas faire des choses aussi compliquées mais que nous allions résoudre un problème similaire.
Je leur ai projeté un énoncé sur le TNI (voir la page 2) tout en leur distribuant le texte sous forme papier et en leur demandant de faire l'activité pour le lendemain.
Je leur ai ensuite projeté la planche de Dürer (voir la page 6) pour leur faire prendre conscience que ce problème avait été posé au 15ième siècle.
Enfin, à la surprise générale, j'ai demandé à ceux qui avaient un téléphone pouvant se connecter en wifi à Internet de ne surtout pas l'oublier le lendemain.
Sans plus de détails, nous sommes passés à tout autre chose.
| Albrecht Dürer (1471-1528) est un peintre, graveur et mathématicien allemand. Après un séjour en Italie, il se passionne pour les mathématiques. Il rédige l'ouvrage : « Underweysung der Messung mit dem Zirkel und Richtscheit ». (« Instruction sur la manière de mesurer à l'aide du compas et de l'équerre ») Dürer décrit dans son ouvrage la manière d'obtenir le tracé de l'ombre d'un cube. Ci-contre la planche illustrant son propos que l'on peut retrouver dans la revue Tangente n°162. | 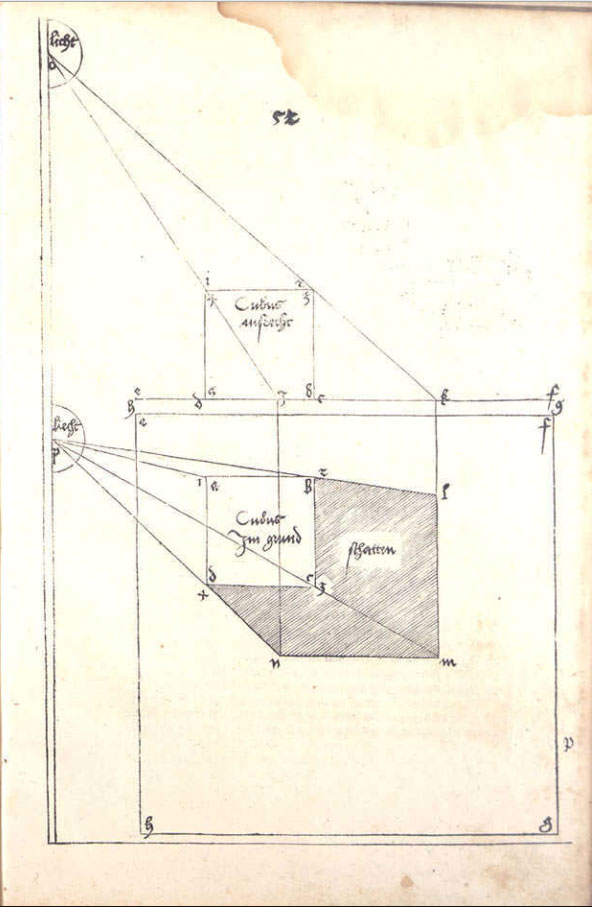 |
Temps 2 : Recherche à la maison
Les élèves ont cherché le problème à la maison de manière à ce que tous aient le temps de se l'approprier.
Temps 3 : Le lendemain, en demi-groupe, dans une salle munie, entre autre, d'un TNI
En début de séance, la vidéo a été, à nouveau, projetée pour «remettre les élèves dans l'ambiance ». Puis ils m'ont présenté rapidement leurs travaux faits à la maison. Tout le monde avait cherché (sans doute grâce à la vidéo) mais tous les élèves n'étaient pas allés jusqu'au bout de l'activité.
Cinq élèves parmi la tête de classe avaient correctement dessiné l'ombre et avaient trouvé le bon résultat pour son aire. Les autres élèves, de niveaux très hétérogènes, n'avaient pas réussi à construire correctement l'ombre en entier.
En résumé, à la maison, tous les élèves avaient dessiné une ombre mais ils avaient finalement fait beaucoup d'erreur dans leurs tracés par manque d'une bonne compréhension de la configuration dans l'espace.
Après ce très rapide passage en revu, j'ai demandé, au grand étonnement de la classe, à deux volontaires :
a. de sortir leur téléphone portable et de se connecter en Wifi à la borne Wifi que j'avais installée dans la salle ;
b. de télécharger l'application IPWebcam ;
c. d'ouvrir l'application IPWebcam et de faire constater à leur camarades que l'écran de la caméra du téléphone était activée et qu'ils pouvaient filmer la salle ;
d. de me donner l'adresse IP qui se trouvait en bas de l'écran qui était apparu sur leur téléphone ;
e. de filmer le pattern (voir la page 7) que je leur avais posé sur leur table puis de regarder l'écran du TNI.
Après plusieurs tentatives infructueuses de la part des élèves, dues sans doute à une erreur de connexion à la borne Wifi, j'ai fait la même chose avec mon propre téléphone. Il est alors apparu sur le tableau numérique l'image de gauche ci-dessous : la figure du problème en réalité augmentée.

Travail donné à faire lors de cette séance (Différentiation pédagogique) :
Au vu du travail très hétérogène fait à la maison, j'ai donc décidé de différencier mes consignes.
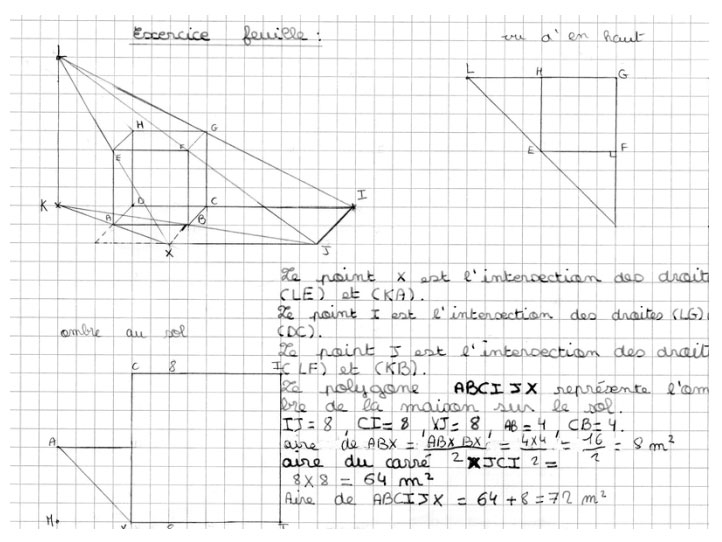
Les élèves qui avaient réussi à trouver la valeur exacte de l'aire de l'ombre devaient, pour ceux qui ne l'avaient pas fait, dessiner l'ombre en vue de dessus puis démontrer que celle-ci était formée d'un triangle isocèle rectangle et d'un carré.
Les élèves qui n'avaient pas su dessiner l'ombre ou s'étaient trompés sur la construction de certains côtés devaient redessiner la figure de base sur leur cahier puis dessiner l'ombre en perspective, puis calculer son aire puis, selon le temps, commencer à justifier sa forme.
La mise au travail a été immédiate dans les deux groupes sans doute parce que chacun avait une tache à faire à sa portée mais aussi, je pense, parce que le dispositif mis en place leur paraissait exceptionel, d'un point de vu technologique.
Il est à noter que tous les élèves ont voulu refaire leur dessin même ceux qui l'avaient fait correctement à la maison. Les élèves se sont tous beaucoup appliqués dans leurs constructions même ceux qui en général ne sont pas très soigneux.
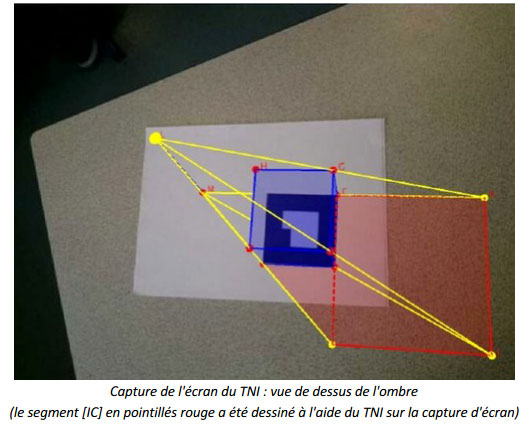
En plus de pouvoir filmer virtuellement la figure et donc de pouvoir tourner autour, j'avais prévu de faire apparaître progressivement les différents traits de construction de la solution à l'aide des touches du clavier de l'ordinateur. Les élèves ont donc été accompagnés dans leur construction. Cependant, la solution n'a jamais été donnée a priori. Des captures d'écran de certaines vues ont été saisies et collées sur le TNI. Cela me permettait d'avoir les mains libres et de dessiner à l'aide des outils du TNI sur les captures d'écran et donc de donner des pistes de réflexion ou des solutions.
Je pense que ce dispositif a permis d'aider les élèves qui ont des difficultés en géométrie dans l'espace. En général, les élèves ont «du mal à voir», à appréhender la représentation en perspective, dans un plan, d'une figure en trois dimensions même avec des logiciels de géométrie dynamique (Geospace, Interesp, Geogebra 3D...). Il m'a semblé que le déplacement du téléphone autour du pattern, c'est à dire virtuellement, le déplacement autour de la figure, a apporté un plus et a permis de débloquer beaucoup d'élèves qui n'auraient pas avancé sans l'apport de la réalité augmentée. Je pense que les élèves kinesthésiques ont eux aussi une chance avec la réalité augmentée de progresser en géométrie dans l'espace.
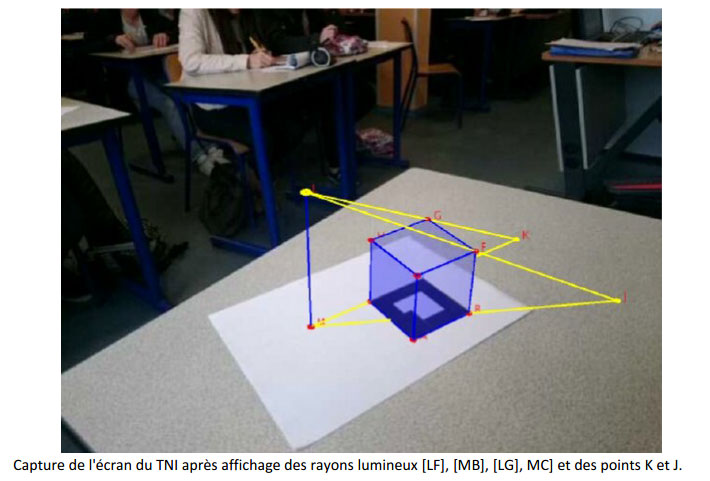
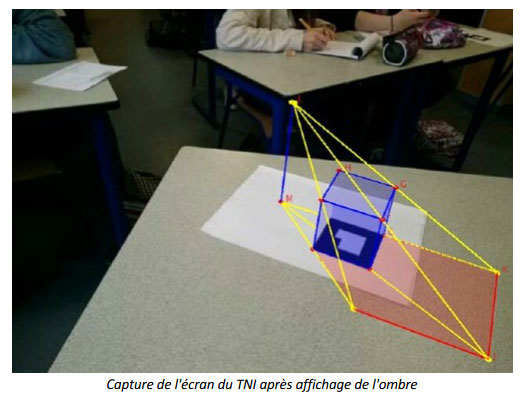
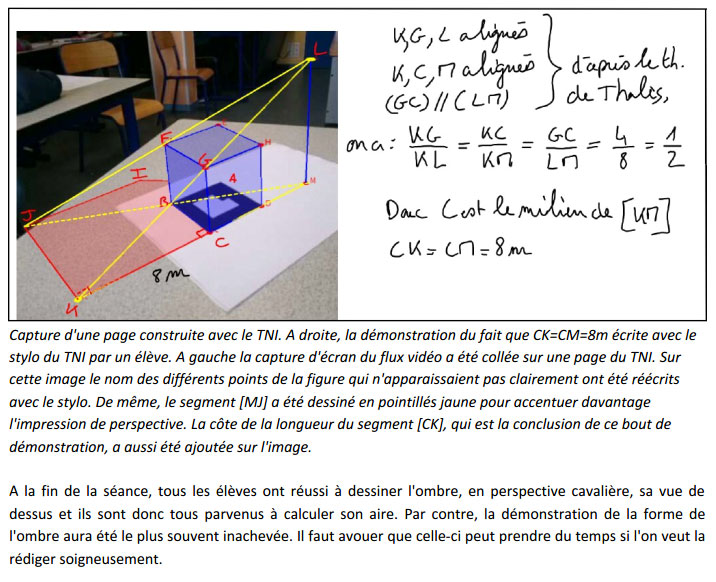
Je les ai fait patienter et chercher. J'ai continué à tourner autour de la figure en filmant de côté. Les élèves ont faits des captures d'écran qu'ils collaient sur le TNI. En dessinant sur les images obtenues, j'ai progressivement réussi à faire comprendre à presque tous le monde que l'ombre de ce cube est en fait un polygone formé d'un carré et d'un triangle isocèle rectangle.
Yann Bertrand, Enseignant au lycée Aristide Briand de St Nazaire
information(s) pédagogique(s)
niveau : tous niveaux, Lycée tous niveaux, 2nde
type pédagogique :
public visé : non précisé, élève, enseignant
contexte d'usage : travail autonome
référence aux programmes :
documents complémentaires
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA


