espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > actions nationales 2015-2017 > 1 séance ou 2
quelques constructions géométriques
mis à jour le 04/01/2016
mots clés : algorithmique, TraAM, déplacement
Contexte et premiers contacts avec l’algorithmique
Les élèves de 4ème et de 3ème n’ont jamais utilisé le logiciel Scratch.
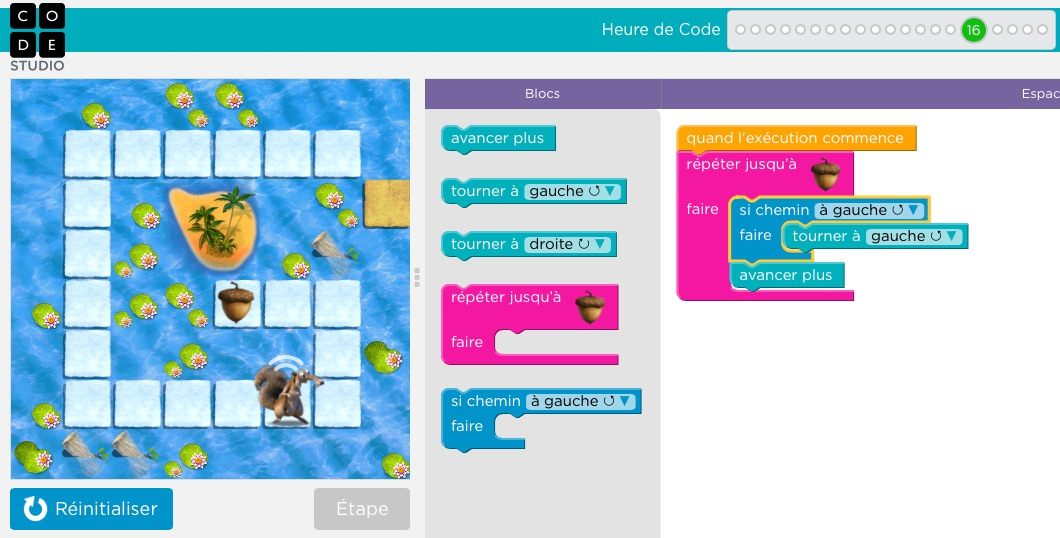
Ils ont cependant été initiés aux outils algorithmiques à l’aide du site « hour of code » (heure de code) : https://studio.code.org/hoc/1 qui propose de résoudre 20 « puzzles » (des labyrinthes) à l’aide de bloc de programmations de déplacements, exactement comme avec l’outil Scratch.
Cet outil en ligne à l’avantage d’introduire de façon très ludique et adaptée à tout âge les éléments nécessaires à la réalisation d’algorithme (déplacements simples, boucles « pour », boucles « jusqu’à », test « si alors sinon… »).
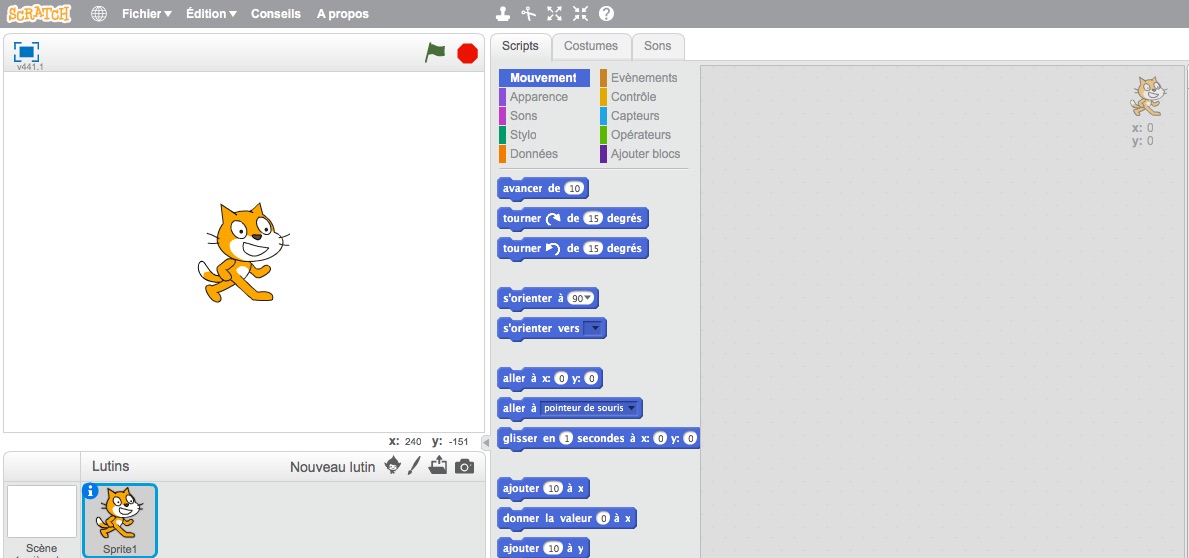
Nous sommes en salle multimédia. Deux élèves par poste (je ne peux pas faire autrement…. : 15 postes pour 28 élèves). L’interface Scratch qu’il découvre ensuite a été présenté une fois en classe et le fonctionnement des blocs (par glisser-déposer) ne pose pas de souci.
On annonce aux élèves qu’on va leur demander de construire des figures géométriques simples en programmant les déplacements du lutin (le chat…).
Première construction : un carré
Sans consigne écrite, sans support visuel (donc oralement…), je demande aux élèves de programmer la construction d’un carré de côté 120 pixels.
Pour cette première manipulation de scratch, deux apports techniques ont de suite été nécessaires :
| L’utilisation d’une commande de démarrage du programme : |  |
| Les options d’écriture du stylo : | 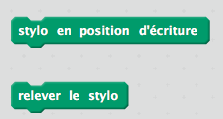 |
Ceci a été abordé oralement et faisant une démonstration rapide au vidéoprojecteur.
Les élèves se lancent rapidement dans des constructions.
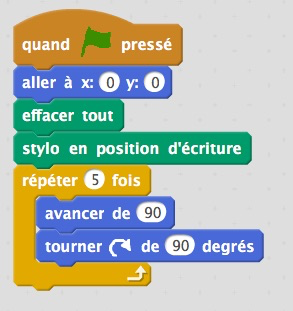
Voici deux exemples de programmes obtenus rapidement :
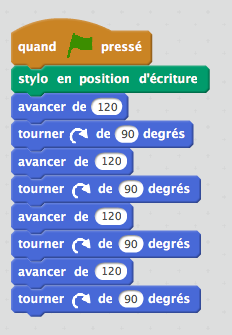 | 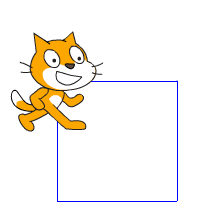 | 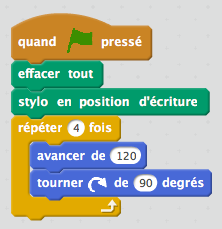 |
Plusieurs élèves s’étonnent de ne pas voir le lutin se déplacer. Je leur parle de la vitesse de déplacement… et montre la commande :
Un point rapide et collectif est fait pour montrer l’intérêt du programme de droite (permettant de répéter plusieurs fois une même série d’instructions).
Cette première activité ne comportait pas de difficulté mathématique, mais elle permet cependant de percevoir la « construction géométrique » d’un certain point de vue, celui de la construction pas à pas et dans un certain ordre d’une figure.
Deuxième construction : un rectangle
La première construction a été très rapide et modulo quelques entraides techniques (toujours autorisées) entre les binômes et par proximité, le carré a été réussi facilement par l’ensemble des élèves.
Je demande donc une seconde figure : un rectangle de longueur 150 pixels et de largeur 90 pixels.
Voici deux exemples de programmes obtenus rapidement :
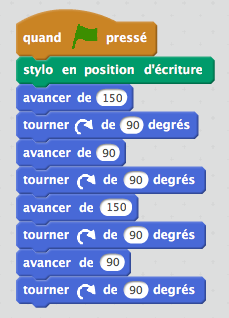 | 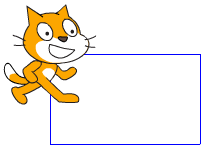 | 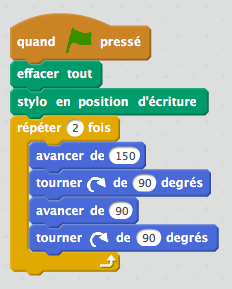 |
A nouveau, un point rapide et collectif est fait pour reparler de la boucle « répéter » (2 fois ici).
A ce stade, tout les élèves me semblent trouver cela très facile… mais je n’ai pas dit mon dernier mot….
Troisième construction : un parallélogramme
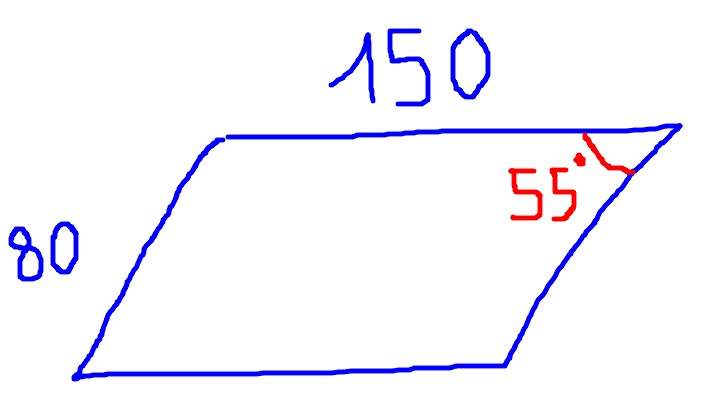
A main, je dessine au tableau la figure suivante :
J’ai à peine le temps de dire quelque chose que le mot « parallélogramme » fuse dans la salle…
Je dit « ok : allez-y… Reproduisez-moi ce parallélogramme dont les côtés mesurent 150 pixels et 80 pixels et ayant un angle de 55° ».
Tout le monde se lance….
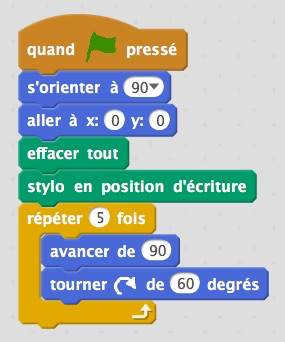
J’observe tranquillement et fais quelques captures d’écran des débuts de programmes que je vois :
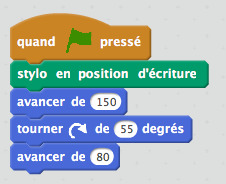 | 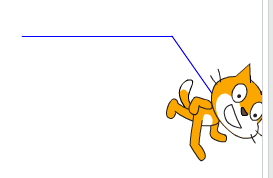 |
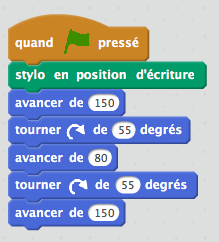 | 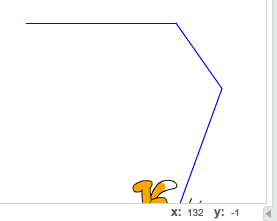 |
Les discussions sur les angles sont nombreuses et le problème est double :
a) l’instruction « tourner de 55 degrés » n’a pas donner l’effet souhaité…
b) la connaissance de la mesure de l’autre peut être un atout…
Un point collectif est réaliser et des solutions potentielles sont proposées par certains élèves :
- « on peut tourner dans l’autre sens… » propose l’un en ayant vu les flèches qui accompagne les blocs « tourner »
pas si évident en fait….
- « l’autre angle fait 115°, non 125° » dit un autre
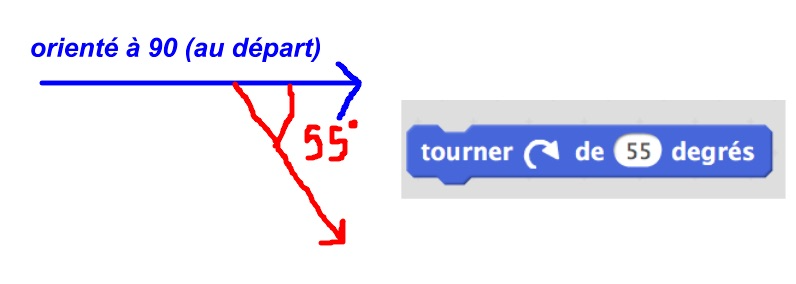
Je me permets d’insister sur le mode de fonctionnement de ces commandes « tourner » en faisant un schéma au tableau :
Les élèves reprennent leurs constructions et plus ou moins rapidement, nous obtenons :
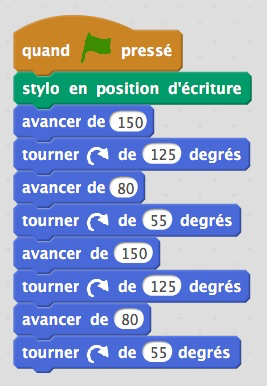 |  | 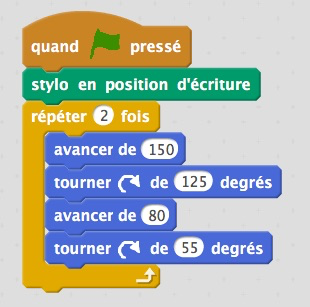 |
Quatrième construction : un pentagone
Pour les plus rapides d’abord, puis au fur à mesure pour tous les binômes, je propose une dernière construction : « une figure à 5 côtés… c’est à dire ?.... »
« Un pentagone ? »
« Bien Laura ! ».
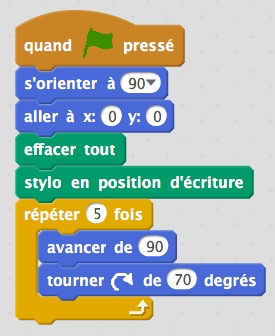
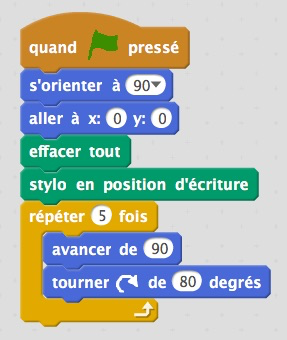
« Je vous propose de réaliser un pentagone dont les 5 côtés mesurent 90 pixels… »
Remarque : je ne dessine rien… je ne précise pas « pentagone régulier » mais tous les élèves le prennent comme tel… Les recherches commencent…
Les élèves n’ont pas traité d’activité sur les angles inscrits, les polygones réguliers… Je m’attendais donc à quelques difficultés…
Après quelques tentatives, ils sentent que c’est la mesure de l’angle qui est la clef…
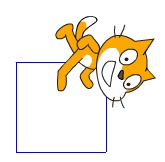
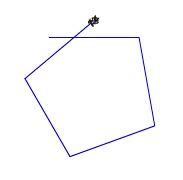
Un groupe m’appelle pour me dire qu’ « ils ont trouvé !!! » mais en diminuant la taille du lutin on voit ceci :
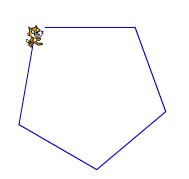
Finalement le 72° est trouvé par plusieurs groupes, mais par tâtonnements.
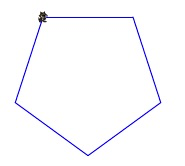
Je prends le temps d’une explication sur papier (que je ne retranscris pas ici) sur le pourquoi de ce 72°…. et je sens les élèves très à l’écoute de cette démonstration.
Ceci me permettant de conclure que cette activité a été, sans l’avoir prévu, une bonne occasion de faire une explication plus « théorique » sur les mesures d’angles dans les polygones réguliers avec une motivation certaine des élèves qui avaient passé un peu de temps à chercher un angle, qu’ils peuvent maintenant expliquer…
Stéphane Percot, Enseignant au Haxo à La Roche sur Yon (85)
information(s) pédagogique(s)
niveau : tous niveaux, Collèges tous niveaux, 4ème, 3ème
type pédagogique : scénario, séquence, non précisé
public visé : non précisé, enseignant, élève
contexte d'usage : salle multimedia
référence aux programmes :
ressources associées

|
quadrilatères | 07/03/2016 |
| Comprendre les angles avec scratch. |
||
| quadrilatère, algorithmique, TraAM | Grégory Maupu | |

|
angles et parallélisme | 07/03/2016 |
| Comprendre les angles avec scratch. |
||
| angles, parallélisme, algorithmique, TraAM | Grégory Maupu | |
documents complémentaires
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA