espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > actions nationales 2007-2009 > Projets de scénarii (lycée)
A la recherche d'un lieu en terminale S
mis à jour le 29/04/2008
Il s'agit d'explorer une situation à l'aide d'un logiciel de géométrie dynamique en repérant les invariants d'une figure et les positions particulières du point mobile.
mots clés : invariant, conjecture, validité, lieu, similitude, complexe
Enoncé l'activité
Dans le plan orienté, on considère deux points distincts A et B .
On appelle I le milieu du segment [AB] et (C) le cercle de diamètre [AB].
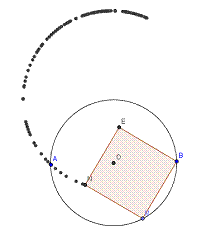
On considère un point M variable, appartenant au cercle (C) et distinct de B et on construit le carré MBEN de sens direct.
Le but de cette activité est de déterminer le lieu du point N.
1.Créer une figure dynamique permettant d'observer le lieu du point N.
Questionnement possible :
La droite (MN) semble passer par un point fixe. Lequel ?
Faire une conjecture sur le lieu du point E.
Faire une première conjecture sur le lieu du point N.
Quelle semble être la particularité de la droite (EM) ?
2.Enoncer une conjecture concernant le lieu du point N
3.Prouver la conjecture précédente.
Objectifs
Il s'agit d'explorer une situation à l'aide d'un logiciel de géométrie dynamique.
Le questionnement proposé permet de repérer des invariants de la figure.
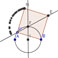
La trace activée du point E permet de conjecturer que le point E décrit un cercle de même rayon que le cercle (C).
On peut conjecturer que le point N décrit un cercle
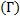 de centre F ayant un rayon environ 1,5 fois plus grand que le rayon de (C). On découvre que la droite (ME) passe par un point fixe qui est le point F.
de centre F ayant un rayon environ 1,5 fois plus grand que le rayon de (C). On découvre que la droite (ME) passe par un point fixe qui est le point F.- Pour les élèves connaissant les similitudes, il suffit de remarquer que le point N est l'image du point M par la similitude directe de centre B, de rapport
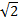 et d'angle
et d'angle 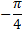 . D'après les propriétés des similitudes, N décrit le cercle
. D'après les propriétés des similitudes, N décrit le cercle 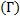 de centre F (image de I par la similitude de centre B, d'angle
de centre F (image de I par la similitude de centre B, d'angle 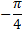 et de rapport
et de rapport 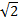 ) et de rayon IA
) et de rayon IA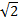 .
.
Le lieu de N est donc le cercle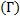 privé du point B.
privé du point B.
Les points E,F,M sont alignés sur la médiatrice du segment [BN]
On obtient facilement l'alignement des points M, A , N. (AMB et NMB sont droits)
Ce dernier alignement permet de construire N connaissant M et le lieu de N.
- Pour les élèves ne connaissant pas les similitudes, la preuve peut aussi se faire avec les nombres complexes en choisissant un « bon » repère c'est à dire par exemple un repère pour lequel on ait : A(-1 ;0) B(1 ;0) et F(0 ;1).
On conjecture l'affixe du centre F de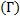 pour commencer la preuve.
pour commencer la preuve.
Quelques vues attendues
Réalisation avec Géogébra :
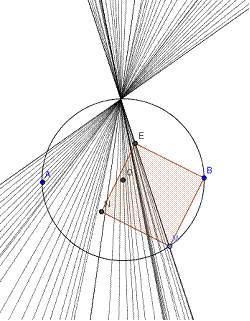
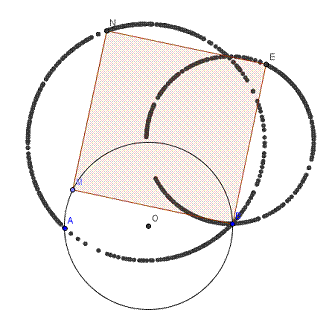
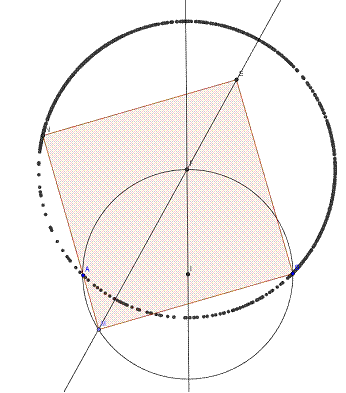
Les compétences expérimentales possibles à évaluer
- Placer un point fixe, un point mobile sur un objet.
- Elaborer une démarche : construire un carré de sens direct.
- Prendre l'initiative d'activer la trace d'un point ou d'une droite.
- Découvrir des invariants d'une figure et les exploiter .
- Tester des cas particuliers.
- Enoncer clairement une conjecture .
- Tester la validité d'une conjecture (ici en traçant le cercle
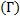 de centre F passant par A et en regardant si le lieu de N coïncide bien avec )
de centre F passant par A et en regardant si le lieu de N coïncide bien avec )
information(s) pédagogique(s)
niveau : Terminale S
type pédagogique : non précisé
public visé : enseignant, élève
contexte d'usage : non précisé
référence aux programmes :
documents complémentaires
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA