espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > actions nationales 2007-2009 > Projets de scénarii (lycée)
En traversant le cube
mis à jour le 27/05/2009
Dans cette activité qui débute par des constructions avec papier-crayon, le logiciel Géospace permet de proposer une correction dynamique qui unifie les différents cas et d'énoncer une conjecture rendue visible par le mode trace.
mots clés : section , cube , plan , géospace
Enoncé l'activité
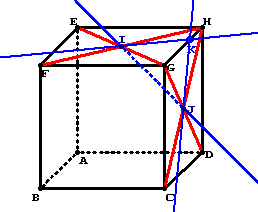
ABCDEFGH est un cube
I désigne le centre de la face carrée EFGH
J désigne le centre de la face carrée GHDC
K désigne un point mobile sur le segment [GH].
Le plan (IJK) coupe le plan (ABC) suivant une droite (d).
Quelle est la particularité de cette droite (d) quand le point K
décrit le segment [GH]?
Contexte
Cette activité se situe au milieu de l'année en classe de seconde.
Les élèves ont déjà tracé de nombreuses sections de tétraèdres et aussi de cubes coupés par un plan.
Pour cette expérimentation, les élèves connaissent le théorème « quand deux plans parallèles sont coupés par un troisième, l'intersection se fait suivant des droites parallèles ». Ils ont fait connaissance avec Géospace mais ils n'ont jamais utilisé la commande « créer une droite d'intersection entre deux plans » ni « créer un polygone convexe intersection d'un solide avec un plan » ni « créer un point intersection d'une droite et d'un plan » .
Scénario
J'ai commencé cette activité par un travail différencié de construction du type « papier-crayon » qui était le prolongement direct d'activités déjà rencontrées dans l'année.
J'ai donc distribué à chaque élève une construction à effectuer, l'emplacement du point K variant d'un élève à l'autre (j'avais inséré quelques cas particuliers intéressants pour la suite : K=H , K=G , K égal au milieu M du segment [GH] , K positionné entre M et G, K positionné entre M et H ...).
La consigne accompagnant
la figure était :
| ABCDEFGH est un cube. I désigne le centre de la face carrée EFGH. J désigne le centre de la face carrée GHDC. K désigne un point du segment [GH]. Construire la droite (d) d'intersection des plans (IJK) et (ABC) . |
Chaque élève a obtenu une droite (d) construite avec crayon et papier et deux stratégies différentes sont apparues suivant qu'on utilise ou pas le théorème « quand deux plans parallèles sont coupés par un troisième, l'intersection se fait suivant des droites parallèles ». (voir annexe)
J'ai présenté ensuite une correction pour chacune des deux stratégies en projetant une construction pas à pas réalisée sous Géospace avec le point K variable sur le segment [GH].
J'ai demandé ensuite aux élèves de réaliser eux-mêmes la construction sous géospace (classe en demi-groupes avec 2 élèves par poste) en utilisant cette fois la commande « créer la droite d'intersection entre deux plans ». C'est la première fois que cette commande était utilisée.
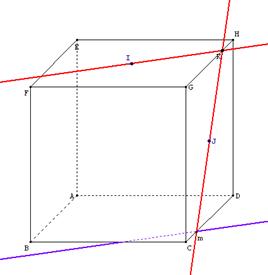
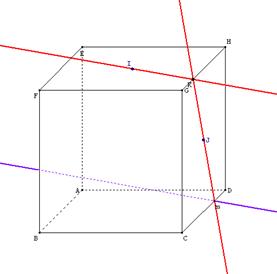
J'ai alors proposé un nouveau travail :
| Quelle est la particularité de la droite (d) quand K décrit le segment [GH]? |
Les élèves font bouger le point K et observent le comportement de la droite (d) sans rien conclure.
Le retour sur quelques cas particuliers provoque débat dans la classe : K=H, K égal au milieu M de [GH].
Un élève pense à sélectionner le mode trace pour la droite (d) et là le résultat est étonnant.
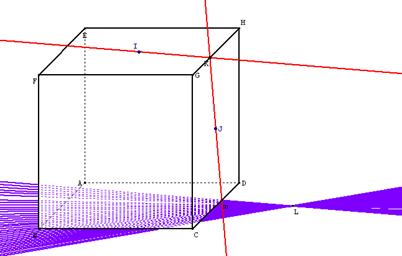
On peut alors conjecturer que les droites (d) passent toutes par un même point.
Preuve attendue
Les droites (d) passent toutes par le point fixe L, intersection de la droite (IJ) avec le plan (ABC).
Construction du point L
Les élèves ont souhaité découvrir la position de ce point L et deux pistes ont été évoquées :
Première idée : le point L est le symétrique du point I par rapport au point J . (preuve par projection de milieu)
Deuxième idée : si on colle à droite du cube ABCDEFGH, un cube identique CDD1C1GHG1H1, le point L apparaît comme le centre de la face carrée CDD1C1.(voir preuve en annexe)
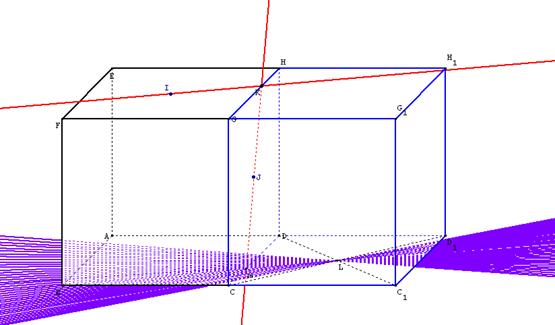
Retour sur le dessin avec « papier-crayon »
Les prolongements précédents permettent d'avoir une construction du point L et chaque élève vérifie que la droite (d) qu'il a construite au début de l'activité passe bien par ce point L.
Compétences expérimentales
- Utiliser un logiciel de géométrie dynamique pour visualiser une situation de l'espace.
- Prendre l'initiative d'observer des cas particuliers
- Prendre l'initiative d'utiliser le mode trace pour découvrir une particularité de la figure.
Prolongement Evaluation
I désigne un point quelconque appartenant à la face carrée EFGH
J désigne un point quelconque appartenant à la face carrée GHDC
Construire l'intersection de la droite (IJ) avec le plan (ABCD)
Gérard Cordes, Enseignant, Lycée Delattre de Tassigny
information(s) pédagogique(s)
niveau : 2nde
type pédagogique : non précisé
public visé : enseignant, élève
contexte d'usage : non précisé
référence aux programmes :
documents complémentaires
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA