espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > actions nationales 2007-2009 > Projets de scénarii (lycée)
Inégalité avec l'exponentielle
mis à jour le 02/05/2008
Comment optimiser un paramètre en faisant le lien entre lareprésentation graphique de la fonction exponentielle et celle d'une famille dedroites.
mots clés : initiative, interpréter, conjecture, robustesse, exponentielle, famille de droites
Enoncé de l'activité
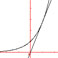
- Obtenir la représentation graphique de la fonction exponentielle à l'aide d'un logiciel de géométrie.
- Vérifier graphiquement si les affirmations suivantes sont vraies ou fausses :
a) 2x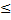 ex pour tout réel x.
ex pour tout réel x.
b) 3x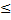 ex pour tout réel x.
ex pour tout réel x. - Conjecturer la valeur à 10-2 près du plus grand réel a tel que : ax
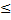 ex pour tout réel x
ex pour tout réel x - Démontrer la conjecture.
Objectifs
Le but de cette activité est d'optimiser un paramètre en faisant le lien avec les représentations graphiques de la fonction exponentielle et d'une famille de droites.
Scénario
1. Ce qui a été fait avant
Les élèves ont déjà travaillé sur ce logiciel de géométrie :
- Deux problèmes d'optimisations dans des situations géométriques ont donné lieu à des créations de variables numériques telles que des abscisses et des aires ainsi qu'à leurs affichages.
- Deux résolutions graphiques d'équations de type f(x) = k ont été élaborées en classe entière (un élève réalisant sur ordinateur les idées émises par la classe). La possibilité de créer une variable numérique pilotée au clavier leur a été présentée à cette occasion.
- Cette séance s'est déroulée quelque temps après que les limites de la fonctions exponentielles aient été établies.
2. Le déroulement
La traduction géométrique des deux premières inégalités n'est pas immédiate, puis l'utilisation de deux droites passant par l'origine se répand dans la classe.
La traduction géométrique de la troisième inégalité donne lieu à plusieurs types de stratégies :
- Certains créent un point libre puis la droite passant par ce point et l'origine et affichent le coefficient directeur de cette droite. Ils déterminent une valeur approchée du paramètre a maximal par pilotage du point à la souris.
- Certains procèdent par essais successifs de modification du coefficient directeur des deux premières droites.
- Des élèves se sont rappelé la création possible d'une variable numérique puis ils ont créé la droite d'équation y = ax.
Les limites de la conjecture laissent ensuite entière place à la démonstration.
La démonstration de la conjecture est laborieuse pour beaucoup d'élèves. Le début de la démarche ne pose pas de problème, les élèves utilisent la fonction intermédiaire définie par
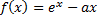 (la fonction intermédiaire
(la fonction intermédiaire 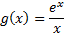 n'a pas été envisagée). La gestion du paramètre a les gêne tous plus ou moins longtemps au moment d'envisager une étude des variations. Chaque élève a pu disposer du temps nécessaire pour surmonter ses blocages. Quelques élèves mènent la démonstration à terme avant la fin de la séance, mais les autres sont à des étapes diverses. Une mise au point sur la mise en œuvre est faite avec tout le groupe et chacun doit poursuivre sa démonstration pour la prochaine séance.
n'a pas été envisagée). La gestion du paramètre a les gêne tous plus ou moins longtemps au moment d'envisager une étude des variations. Chaque élève a pu disposer du temps nécessaire pour surmonter ses blocages. Quelques élèves mènent la démonstration à terme avant la fin de la séance, mais les autres sont à des étapes diverses. Une mise au point sur la mise en œuvre est faite avec tout le groupe et chacun doit poursuivre sa démonstration pour la prochaine séance. La pertinence du logiciel de géométrie
Le logiciel de géométrie permet d'émettre une conjecture plus précise que la plupart des calculatrices. Il permet aux élèves de mieux aborder la notion de paramètre en visualisant facilement un grand nombre de représentations graphiques. La visualisation rapide des représentations graphiques laisse ensuite le temps nécessaire au travail de démonstration.
Compétences expérimentales mises en œuvre
- Prendre l'initiative d'interpréter graphiquement une inégalité fonctionnelle.
- Prendre l'initiative d'agir sur la précision de la variable (pilotée au clavier ou par un curseur).
- Tester la robustesse d'une conjecture par utilisation de zoom.
information(s) pédagogique(s)
niveau : Terminale S
type pédagogique : scénario, séquence
public visé : enseignant, élève
contexte d'usage : salle multimedia
référence aux programmes :
documents complémentaires
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA