espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > actions nationales 2007-2009 > Projets de scénarii (lycée)
Jauger un réservoir
mis à jour le 27/05/2009
Avec Géospace, les élèves s'approprient la situation et avancent des conjectures. Le passage au tableur contraint à l'identification des variables , permet d'affiner les conjectures et de visualiser des accroissements de plus en plus petits. Enfin le calcul formel fournit plusieurs écritures d'une même expression algébrique et ouvre ainsi le chemin vers la preuve demandée.
mots clés : fonction, espace, calcul formel
Enoncé l'activité
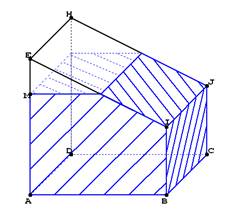
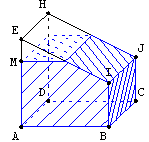
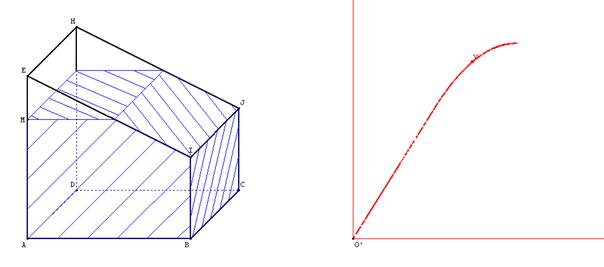
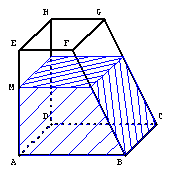
Un réservoir peut être modélisé par le solide ci-dessus.
Les dimensions en centimètres sont: AB=40, BC=40, AE=40, BI=20, CJ=20.
Les faces ABCD et ADHE sont carrées, les faces IJHE et IJBC sont rectangulaires, les faces ABIE et DCJH sont des trapèzes rectangles.
La position du point M sur le segment [AE] est visible de l'extérieur du réservoir.
a)Quelle est la hauteur AM du liquide quand le réservoir est rempli aux trois quarts ?
b) Construire le long de [AE] une graduation qui indique le volume du réservoir de 4 litres en 4 litres.
Objectifs
Il s'agit de faire fonctionner plusieurs concepts de la classe de seconde à travers une situation riche : notion de variable, tableau de valeurs, fonction, courbe représentative d'une fonction, résolution graphique d'une équation, résolution algébrique d'une équation, différentes écritures d'une expression. L'exploration avec un logiciel de géométrie dynamique ouvre la voie à des conjectures, l'utilisation d'un tableur permet d'affiner la conjecture, la mobilisation du calcul formel permet de bien mener la preuve en exploitant les différentes écritures d'une même expression algébrique.
Scénario
Le texte de l'activité est distribué et l'animation faite sous géospace permet de mieux s'approprier la situation.
S'approprier la situation avec le logiciel géospace :
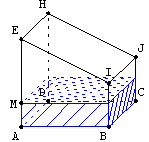
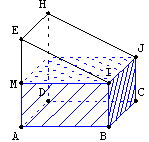
Vers une conjecture :
Pour le a), les élèves conjecturent très vite que la longueur AM est comprise entre 20 et 30. On peut affiner la conjecture en faisant afficher les valeurs de AM et celles du volume correspondant en litres.
On arrive à une longueur AM comprise entre 22,6 et 22,7.
Affiner la conjecture :
Certains parlent de tableur pour obtenir un meilleur encadrement mais il faudrait alors exprimer le volume de liquide en fonction de la longueur AM. L'expression « en fonction de » est lâchée : on note x la longueur AM en cm ( avec x compris entre 0 et 40) et V(x) le volume de liquide en litres.
Le cas
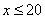 est facile : le volume est
est facile : le volume est 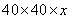 d'où le résultat en litres : V(x) = 1,6x
d'où le résultat en litres : V(x) = 1,6xOn travaille alors à exprimer V(x) en fonction de x pour x>20 : après utilisation du théorème de Thalès et rappels sur le volume d'un prisme, plusieurs expressions viennent dont :
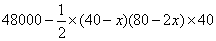 ou
ou 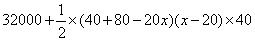 ou
ou 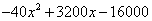 d'où le volume exprimé en litres :
d'où le volume exprimé en litres : 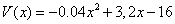 .
.Le tableur permet des approximations successives et la conjecture suivante (Voir annexe) :
« Quand le réservoir est rempli aux trois quarts (36 litres), AM est compris entre 22.6 et 22.7 cm »
Certains pensent à faire une représentation graphique de la fonction f sur calculatrice (les élèves ont déjà rencontré des fonctions définies par morceaux). Le graphique est confirmé par géospace .
C'est le haut du graphique qui étonne : pour l'expliquer je reviens au tableur, en ouvrant une nouvelle colonne de différences
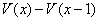 (voir annexe).
(voir annexe).La preuve assistée par ordinateur :
Trouver la hauteur de liquide quand le réservoir est rempli aux trois quart revient à résoudre l'équation : V(x)=36 ou encore :
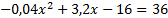 soit :
soit : 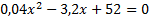 .
.L'équation est difficile à résoudre en seconde : les élèves pensent à une factorisation mais n'arrivent pas à factoriser : on fait appel à un logiciel de calcul formel comme Xcas .

Ce premier résultat est rassurant car on retrouve une solution voisine de 22.7 mais la factorisation n'est pas exacte ( il suffit de raisonner sur les derniers chiffres du produit
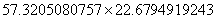 .
.Je suggère la commande forme canonique déjà rencontrée :
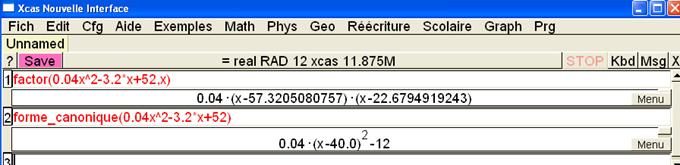
Le problème revient à résoudre l'équation
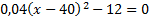 ou
ou 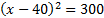 . Avec cette nouvelle écriture, l'élève de seconde peut terminer et conclure que la valeur exacte de la solution est :
. Avec cette nouvelle écriture, l'élève de seconde peut terminer et conclure que la valeur exacte de la solution est : 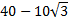 .
.Remarque 1 : En écrivant V(x)-36 sous la forme,
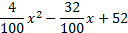 , on obtient une factorisation plus exacte :
, on obtient une factorisation plus exacte : Remarque2 : On aurait pu choisir d'utiliser l'instruction Solve, mais cette instruction ressemble davantage à une boîte noire car on maîtrise moins la nature de la tâche effectuée par le logiciel.
Remarque 3 : Pour fabriquer la jauge, les élèves résolvent équations
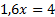 , ...,
, ..., 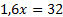 .
. Puis ils choisissent de continuer avec Xcas pour résoudre les équations :
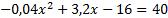 ,
, 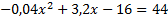 ,
, 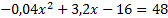 (voir Annexe)
(voir Annexe)Pour cette question, la tâche est répétitive, les élèves utiliseront l'instruction solve de Xcas.

Compétences expérimentales
- Utiliser des cas particulier pour énoncer une première conjecture.
- Prendre l'initiative d'utiliser un tableur pour mener une démarche d'approximations successives.
- Prendre l'initiative d'afficher des grandeurs géométriques pour affiner une conjecture.
- Prendre l'initiative d'utiliser la trace d'un point pour visualiser une courbe.
- Prendre l'initiative d'utiliser un tableur pour examiner les différences successives et comprendre la vitesse de croissance.
- Prendre l'initiative de mobiliser un logiciel de calcul formel pour obtenir plusieurs écritures d'une même expression ( factorisation, forme canonique).
- Avoir une analyse critique des différentes expressions produites par un logiciel de calcul formel. Choisir l'écriture algébrique la mieux adaptée pour résoudre un problème.
Piste pour une évaluation
On peut proposer cette situation voisine avec le même énoncé.
Gérard Cordes, Enseignant, Lycée Delattre de Tassigny
information(s) pédagogique(s)
niveau : 2nde
type pédagogique : non précisé
public visé : enseignant, élève
contexte d'usage : non précisé
référence aux programmes :
documents complémentaires
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA