espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > actions nationales 2007-2009 > Projets de scénarii (lycée)
Les cars de supporters
mis à jour le 09/04/2008
Une situation concrète qui permet de donner du sens à la notion de fonction définie par morceaux. L'analyse comparative de différents types de représentations conduit à des échanges fructueux.
mots clés : tableur, coût marginal, croissance, continuité, calculatrice, fonction, nuage de points
Enoncé de l'activité
En SECONDE :
- Représenter graphiquement le nombre de cars en fonction du nombre de supporters.(unités:1cm pour 10 supporters en abscisse et 1 cm pour 1 car en ordonnées)
- Chaque car se loue 800€. Combien l'organisateur peut-il accepter de supporters, s'il s'est engagé à ce que le prix d'une place ne dépasse pas 20€ ?
En TES :
Combien l'organisateur peut-il accepter de supporters, s'il s'est engagé à ce que le prix d'une place ne dépasse pas 20€ ?
Présenter vos conclusions de façon synthétique.
Objectifs
Pour les TES c'est l'occasion d'aborder, à partir d'une situation très simple, les notions de continuité, de croissance, de coût marginal...
Scénario
En seconde, cette activité se déroule sur deux séances de modules, en salle informatique, les postes étant équipés d'Excel et de sinequanon. Les élèves peuvent aussi utiliser leur calculatrice graphique. La première question permet au professeur de présenter quelques détails techniques qui pourront être réinvestis dans la deuxième question.
En TES, l'énoncé a été donné sans la première question sous la forme d'un exercice à chercher pour la séance suivante. L'exploitation s'est faite en classe entière avec vidéoprojecteur, les 34 élèves ayant leur calculatrice habituelle.
Je décris ici brièvement le déroulement des deux séances en classe de seconde.
Un compte rendu plus détaillé d'une première expérimentation figure en annexe avec un énoncé un peu différent.
1. Ce qui a été fait avant
2. Le déroulement
Le premier réflexe n'est pas d'utiliser un tableur.
Certains sortent une calculatrice graphique : mais quelle fonction saisir sur cette calculatrice ?
Ils reviennent vite à une feuille de papier et tracent d'abord quelques points puis complètent et souvent relient un peu vite. Petit à petit les graphiques se font plus précis et les points de rupture apparaissent.
Certains relient les points pour arriver à une courbe d'autres en restent à des points.
On utilise alors en même temps dans la classe : un tableur, un grapheur et les calculatrices graphiques
Sur ces productions les questions mathématiques sont fort intéressantes en particulier :
comment représenter les zones de rupture ?
comment enlever les « bavures » des graphiques obtenus par la calculatrice ?
Comparaison des écrans obtenus suivant le réglage en mode « connected »
ou en mode « dot ».
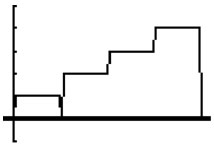
Au départ des résultats exacts sont lancés sans qu'une méthode soit mise en place.
Pour y voir plus clair, les élèves ont recours au tableur puis à une modélisation par une fonction définie par morceaux. Beaucoup de discussions naissent autour des représentations obtenues et le graphique dans sa globalité apporte une vision d'ensemble de cette tarification et des réflexions intéressantes.
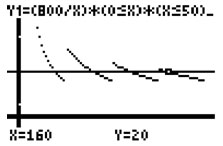
« le prix ne descend jamais au dessous de 16€ même si les supporters sont très nombreux. »
« normalement, plus on est nombreux, moins on paye cher : ici ce n'est pas vrai»
« parfois, quand on a un supporter de plus, on paye plus cher et parfois c'est le contraire »
La conclusion sous forme de réunion d'intervalles a été difficile à mettre en place en seconde, mais cette réunion d'intervalles a du sens.
Remarque : les fonctions évoluées du tableur n'ont pas été utilisées ici mais on pourrait imaginer d'autres scénarios faisant appel à la structure conditionnelle ou à la fonction partie entière. J'ai observé qu'une utilisation très simple du tableur permet de bien s'approprier le problème.
Compétences expérimentales à évaluer
Utiliser un tableur pour organiser, traiter, synthétiser des données.
Prendre l'initiative de mener une analyse comparative de deux types de représentation.
Prendre l'initiative de faire une analyse critique d'une représentation.
Prendre l'initiative d'établir un lien entre des données numériques et un nuage de points.
Choisir un mode de représentation adapté (nuage ou modélisation par une fonction).
Prendre des initiatives . Ici : tester, organiser des essais.
information(s) pédagogique(s)
niveau : 2nde, Terminale ES
type pédagogique : non précisé
public visé : enseignant, élève
contexte d'usage : classe, salle multimedia
référence aux programmes :
documents complémentaires
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA


