mathématiques

espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > actions nationales 2007-2009 > Projets de scénarii (lycée)

Lieu d'un orthocentre

mis à jour le 15/05/2008

A partir d'objets familiers, on étudie un lieu géométrique . Un logiciel de géométrie dynamique permet de découvrir un translation intéressante.

mots clés : conjecture, orthocentre, translation, cercle, parallélogramme, lieu

Enoncé de l'activité

On considère un cercle de centre O et de diamètre [AB]. Sur ce cercle , on place un point fixe C et un point mobile M.
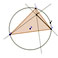
Tracer l'orthocentre H du triangle ACM.
Quel est le lieu géométrique décrit par H quand M décrit le cercle ?

Objectifs

Découvrir l'existence et la nature de la transformation du plan qui transforme le point M en le point H .
Conjecturer la nature du lieu géométrique du point H quand M décrit le cercle privé des points A et C .
Démontrer cette conjecture.

Déroulement du scénario

Les élèves travaillent avec géogébra . Ils n'ont pas de mal à construire une figure dynamique : les notions de point fixe et point mobile sur un cercle ont déjà été rencontrées ainsi que l'utilisation des outils de construction.
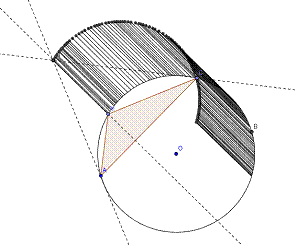
En faisant bouger le point M sur le cercle () de diamètre [AB], ils s'aperçoivent que le point H décrit un cercle. Pour mieux visualiser ce cercle, ils demandent une trace active du point H. Ils découvrent que H semble se déplacer sur un cercle de même rayon que (). Il reste à découvrir le centre de ce nouveau cercle.
Certains élèves, voulant sans doute tester des cas particuliers, se demandent ce qui se passe quand M est en A ou en C.
D'autres commencent à repérer des invariants : « la distance entre H et M, elle ne bouge pas » . Puis encore mieux : « le vecteur

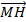est fixe » et enfin « le vecteur

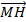est toujours égal au vecteur

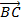». Cette idée est consolidée en activant la trace du vecteur

.
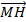Le mot translation apparaît. Le point H est sans doute l'image du point M par la translation de vecteur

.
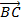Certains ont tracé le quadrilatère MHCB : cette idée est communiquée à l'ensemble de la classe.
Le quadrilatère MHCB ressemble tout à fait à un parallélogramme.

Les idées pour établir la preuve de ce résultat sont longues à venir : dans ce contexte, les élèves ont du mal à reconnaître les propriétés d'un triangle inscrit dans un cercle de diamètre [AB] et à utiliser les propriétés de l'orthocentre. Ainsi les droites (BC) et (MH) sont parallèles car elles sont toutes les deux perpendiculaires à (AC) et il en est de même pour les droites (CH) et (BM) qui sont toutes les deux perpendiculaires à (AM).

Il reste à rédiger en tenant compte des cas particuliers évoqués plus haut (M distinct de A et de C)

Exemples de productions

Avec Géogébra

Avec TInspire

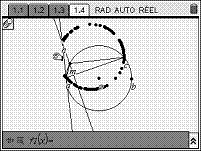
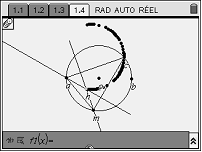
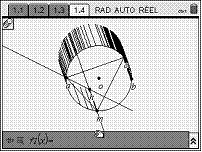
Compétences expérimentales pouvant être évaluées

Expérimenter une situation de géométrie dynamique
Placer un point fixe, un point mobile sur un objet.
Utiliser les outils de construction d'un logiciel de géométrie dynamique.
Tester des cas particuliers.
Prendre l'initiative d'utiliser la fonction trace ou lieu
Repérer les invariants d'une figure ( ici longueur MH ou vecteur )
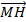Reconnaître une figure clé dans une situation plus complexe (ici parallélogramme MHCB)
Enoncer clairement des conjectures.
Tester la validité d'une conjecture (ici en traçant le cercle (') image de () par la translation de vecteur 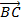et en regardant si le lieu de H coïncide bien avec ('))

Compétences mathématiques pouvant être évaluées

Propriétés d'un orthocentre.
Reconnaître et utiliser une translation
Propriété d'un point appartenant à un cercle de diamètre [AB]
Prouver qu'un quadrilatère est un parallélogramme.
Prendre en compte les cas où l'orthocentre n'existe pas ( M distinct de A et de C)

auteur(s) :

Gérard Cordes