mathématiques
s'identifier
portail personnel ETNA
espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > actions nationales 2007-2009 > Projets de scénarii (lycée)
Recherche de cycles dans un trinôme
mis à jour le 24/04/2009
Tableur, grapheur et calcul formel, tous ces outils sont mis en oeuvre pour résoudre ce problème ouvert donné en terminale S.
mots clés : trinôme, composition, calcul formel, tableur, factoriser
Enoncé l'activité
On considère la fonction f définie sur R par :
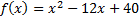.Rechercher les réels a et b vérifiant à la fois :
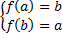
Objectifs
Les pistes proposées par les élèves sont très différentes et font appel à plusieurs logiciels (essais de plusieurs valeurs de x, grapheur , tableur, calcul formel). Les éclairages apportés par différents logiciels vont se compléter pour conduire l'élève à une conjecture de plus en plus fine.
Le problème revient en fait à la recherche des points fixes de
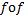et l'intervention du calcul formel est précieuse.
Scénario
Première séance en salle informatique
classe en demi-groupes avec un élève par poste
On peut observer cinq démarrages distincts :
On peut observer cinq démarrages distincts :
- Certains élèves posent le système :
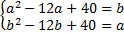avec des difficultés pour le résoudre même avec le logiciel de calcul formel Xcas qui ne traite que les systèmes linéaires.
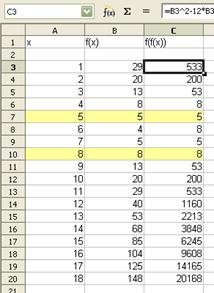
- D'autres élèves utilisent un tableur en ouvrant une première colonne avec des valeurs de x, une deuxième colonne avec des valeurs de f(x), puis une troisième colonne avec les valeurs de f(f(x)) et l'idée vient de regarder s'il y a des valeurs de x telles que f(f(x))= x. Les élèves trouvent deux valeurs 5 et 8 et certains pensent avoir terminé...
Le débat s'installe...Certains remarquent que les deux valeurs trouvées 5 et 8 vérifient f (x) = x et que l'équation f (x) = x n'a que ces deux solutions... D'autres proposent de résoudre l'équation f(f(x)) = x par Xcas.
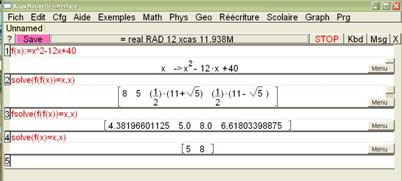
- C'est la troisième piste : résoudre l'équation f(f(x)) = x par le logiciel de calcul formel Xcas.
Et là , on n'est pas déçu . Quatre solutions apparaissent : les deux solutions attendues 8 et 5 et deux autres solutions étonnantes :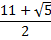
et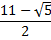 
.
- Le quatrième angle d'attaque du problème est plus graphique, avec par exemple géogébra. Quelques élèves (en petit nombre) ont tracé la représentation graphique de la fonction f, puis ont représenté un réel a variable sur l'axe des abscisses et le réel f(a) puis... des difficultés techniques pour continuer. Ce travail sera abordé lors de la deuxième séance en salle informatique.
Deuxième séance en salle informatique
classe en demi-groupes avec un élève par poste
On trace la représentation graphique de la fonction f, puis on choisit un réel mobile a sur l'axe des abscisses. Ensuite on construit géométriquement f(a) et on « rapporte » ce nombre sur l'axe des abscisses grâce à la droite d'équation y = x .
Par le même procédé, on construit f(f(a )) et ,toujours grâce à la droite d'équation y = x, on « rapporte » ce nombre f(f(a )) sur l'axe des abscisses .
On constate ensuite que a et f(f(a )) coïncident quatre fois.
Quand les élèves ont bien compris que le problème revient à résoudre l'équation f(f(x))=x, une nouvelle idée apparaît et c'est seulement dans cette séance que cela se produit: observer les points d'intersection entre la courbe représentative de la fonction fof et la droite d'équation y = x .
On trace la représentation graphique de la fonction f, puis on choisit un réel mobile a sur l'axe des abscisses. Ensuite on construit géométriquement f(a) et on « rapporte » ce nombre sur l'axe des abscisses grâce à la droite d'équation y = x .
Par le même procédé, on construit f(f(a )) et ,toujours grâce à la droite d'équation y = x, on « rapporte » ce nombre f(f(a )) sur l'axe des abscisses .
On constate ensuite que a et f(f(a )) coïncident quatre fois.
Quand les élèves ont bien compris que le problème revient à résoudre l'équation f(f(x))=x, une nouvelle idée apparaît et c'est seulement dans cette séance que cela se produit: observer les points d'intersection entre la courbe représentative de la fonction fof et la droite d'équation y = x .
En guise d'évaluation
On peut proposer le texte de cette activité en devoir à la maison en demandant une narration de recherche suivie d'une preuve des résultats conjecturés.
Voici les principales idées rencontrées dans les narrations de recherche (voir travaux des élèves en annexe)
- En utilisant le tableur, on obtient deux solutions 5 et 8 mais il doit sans doute y avoir d'autres solutions...
On remarque que 5 et 8 vérifient f(f(5))=f(5)=5 et f(f(8))=f(8)=8.
On explique que si un nombre a vérifie f(a)=a, alors f(f(a))=a donc a et b =f(a) sont solutions du problème.
Ici l'équation f(x)=x n'a que deux solutions 5 et 8 donc il existe exactement deux solutions au problème qui vérifient en plus f(x)=x. - En utilisant un logiciel de calcul formel on découvre deux autres solutions on peut donc conjecturer l'existence de quatre solutions.
- Cette conjecture se confirme en regardant, avec un grapheur, le nombre de points d'intersection entre la courbe représentative de la fonction fof avec la droite d'équation y = x.
On peut aussi s'assurer de cette conjecture avec un logiciel de géométrie dynamique : on construit le réel à partir de a en utilisant la courbe représentative de f et la droite d'équation y = x . On observe que les réels a et f(f(a)) coïncident quatre fois. - On passe ensuite à la preuve. Le problème revient à résoudre l'équation : f(f(x))=x
On commence le calcul de f(f(x))-x en vérifiant éventuellement avec un logiciel de calcul formel.
On obtient un polynôme de degré 4 dont on connaît deux racines 5 et 8 ( les deux solutions de l'équation f(x)=x).
Ce polynôme de degré 4 doit donc être factorisable par (x-8)(x-5).On peut obtenir cette factorisation par un logiciel de calcul formel et en vérifier l'exactitude ou encore procéder par identification.
Le polynôme f(f(x))-x étant factorisé, on obtient rapidement les quatre solutions.
Les compétences TICE à évaluer
Prendre l'initiative d'utiliser un tableur et interpréter les résultats des calculs.
Elaborer une analyse critique d'un résultat.
Apprendre à utiliser un logiciel de calcul formel pour accompagner et vérifier de longs calculs.
Prendre l'initiative d'utiliser un logiciel de calcul formel pour factoriser un polynôme de degré 4.
Confronter les résultats de différents logiciels pour bâtir un raisonnement mathématique complet.
Les compétences Mathématiques à évaluer
Composition des fonctions
Interprétation graphique des équations f(x) = x et de f(f(x)) = x en utilisant la droite d'équation y = x .
Choisir une écriture factorisée pour résoudre une équation polynomiale de degré 4.
Utiliser deux racines connues pour factoriser un polynôme de degré 4.
Gérard Cordes, Enseignant, lycée De Lattre de Tassigny, La Roche sur Yon
information(s) pédagogique(s)
niveau : Terminale S, 1ère S
type pédagogique : non précisé
public visé : enseignant, élève
contexte d'usage :
référence aux programmes :
documents complémentaires
| Les fichiers associés |
Scénario complet 
Deux illustrations sous geogebra :
Cycles d'un trinôme 
Recherche des rééls a et b |
mathématiques - Rectorat de l'Académie de Nantes