Contenu

mathématiques

Recherche simple Vous recherchez ...

espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > actions nationales 2011-2012

comptons les points

mis à jour le 30/04/2012


image010 (Copier).jpg

Quand tout va mal avec les suites, il faut parfois avoir recours à l'outil informatique et plus particulièrement l'algorithmie pour résoudre le problème demandé.

mots clés : TraAM, suite, algorithmique, algorithme, aire, disque, pi

traam

Compétence calculatoire travaillée ou en lien avec ces activités

Il s'agit de la résolution d'un problème ouvert au cours de laquelle les élèves sont conduits à identifier le caractère inopérant de tout ce qu'ils connaissent sur les suites : le modèle mathématique n'est ni une suite géométrique, ni une suite arithmétique, ni une suite définie par une relation de récurrence.

  • Le dénombrement demandé nécessite l'élaboration d'une démarche algorithmique.
  • Mobilisation pertinente de l'outil algorithmique pour effectuer un comptage de points à coordonnées entières dans un disque.
  • Suite définie géométriquement dont les termes peuvent être calculés par un procédé algorithmique.
  • Problème de seuil pour une suite croissante.

Descriptif rapide

A partir d'une situation concrète, l'élève découvre qu'un traitement algorithmique s'impose pour le comptage des points à l'intérieur d'un disque. Ce comptage, associé à l'utilisation d'un quadrillage, permet d'approcher l'aire d'un disque ou le nombre nombre pi.
 

Enoncé donné aux élèves

Le plan est muni d'un repère orthonormé (O ;I ;J) d'unité 1cm. image 1
On se donne un entier naturel n non nul.

On se propose compter le nombre de points à coordonnées entières contenus dans le disque de centre O et de rayon racine carrée de n.

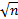  1. Imaginer une méthode de calcul qui permette de calculer le nombre de points à coordonnées entières contenus dans le disque de centre O et de rayon racine carrée de n.
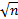  2. Comment choisir l'entier n pour que le disque de centre O et de rayon 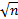racine carrée de n contienne au moins 1000 points à coordonnées entières ?
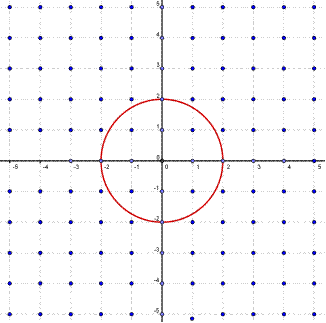
  3. Les figures suivantes obtenues pour n=8 et n=10 permettent de considérer que, pour les grandes valeurs de n, l'aire du disque exprimée en cm2 est voisine du nombre de points à coordonnées entières contenus dans le disque de centre O et de rayon racine carrée de n.
 image 2  image 3

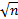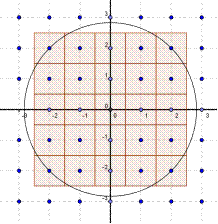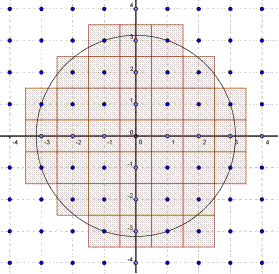Utiliser la méthode de comptage des points précédent pour donner une évaluation grossière du nombre 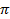nombre pi en choisissant n assez grand (par exemple n=1000).
 
 

Objectifs

Mettre en œuvre une recherche de façon autonome, mener des raisonnements, avoir une attitude critique vis-à-vis des résultats, utiliser l'algorithmique.
Cette activité sous forme ouverte vise prioritairement à renforcer la maitrise des compétences de résolution de problèmes. Elle permet l'utilisation incontournable d'une démarche algorithmique.
 

Vous pouvez accéder au scénario complet ci-dessous...
 
auteur(s) :

Gérard CORDES, enseignant au lycée Jean De Lattre de Tassigny (La Roche sur Yon)

information(s) pédagogique(s)

niveau : 1ère S, 2nde

type pédagogique : non précisé

public visé : enseignant, élève

contexte d'usage : classe, salle multimedia, atelier

référence aux programmes :

documents complémentaires

le scénario complet
PDF le scénario complet

haut de page

mathématiques - Rectorat de l'Académie de Nantes