mathématiques

espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > actions nationales 2011-2012

une histoire d'aire

mis à jour le 29/04/2012

Dans ce problème, les élèves sont amenés à générer une suite récurrente et à découvrir une grande variété de modes de génération de cette suite. Les calculs de termes successifs peuvent s'effectuer à la main, avec la calculatrice ou à l'aide d'un algorithme.

mots clés : TraAM, suite récurrente, suite géométrique, somme de termes, calcul de termes, algorithmique, algorithme, limite d’une suite

Compétence calculatoire travaillée ou en lien avec ces activités

Suites géométriques, somme de termes, suites récurrentes, algorithmique

Descriptif rapide

Dans ce problème, les élèves doivent déterminer la valeur du 15ème terme d'une suite, obtenue par découpages successifs de l'aire d'une figure, puis déterminer l'expression explicite de la suite et sa limite.

Enoncé donné aux élèves

On effectue un coloriage en plusieurs étapes d'un carré de côté de longueur 2 cm.

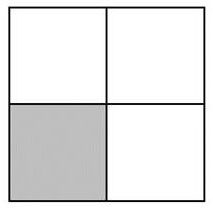
Première étape du coloriage :
On partage ce carré en quatre carrés de même aire et on colorie le carré situé en bac à gauche comme indiqué sur la première figure ci-contre (la figure n'est pas à l'échelle).

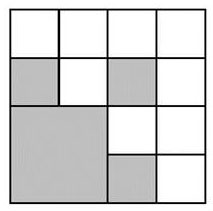
Deuxième étape du coloriage :
On partage chaque carré non encore colorié en quatre carrés de même aire et on colorie dans chacun, le carré en bas à gauche, comme indiqué sur la seconde figure ci-contre.

On poursuit les étapes du coloriage en continuant le même procédé.

Calculer l'aire totale coloriée à l'étape 15.
Déterminer l'expression de l'aire totale coloriée à l'étape n en fonction de n.
Vers quelle limite tend l'aire totale coloriée quand n tend vers + ?

1ère étape

2ème étape

Objectifs

Cette activité posée sous une forme ouverte (ou tâche complexe) vise prioritairement à renforcer la maîtrise des compétences de résolution de problème.
Elle permet de donner sens à la notion de suite et de justifier l'utilisation de la formule qui permet de calculer la somme des termes d'une suite géométrique.
L'automatisation de la mise en œuvre d'un algorithme pour calculer des termes d'une suite récurrente sera ensuite à travailler plus spécifiquement en fonction des besoins des élèves.

Vous pouvez accéder au scénario complet ci-dessous...

auteur(s) :

Olivier PINSON, enseignant au lycée Auguste et Jean Renoir (Angers)

information(s) pédagogique(s)

niveau : Terminale S

type pédagogique : non précisé

public visé : enseignant, élève

contexte d'usage : classe, salle multimedia, atelier

référence aux programmes :

documents complémentaires

le scénario complet

le scénario complet

haut de page

mathématiques - Rectorat de l'Académie de Nantes