espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > actions nationales 2015-2017 > 1 séance ou 2
mur et pavages
mis à jour le 19/04/2016
mots clés : algorithmique, TraAM, déplacement
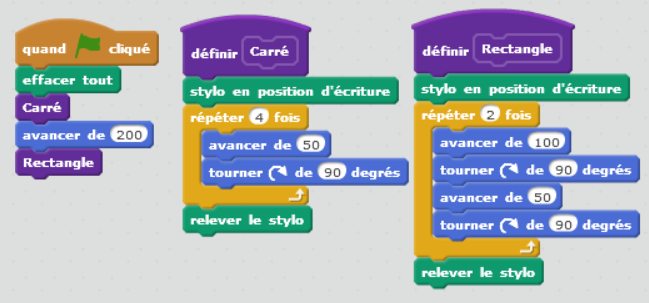
Première construction : un carré
| Sans consignes écrites, et sans que les élèves (ici de 4ème) n’aient de connaissances du logiciel scratch, je montre comment dessiner une ligne brisée en avançant d’un certain nombre de pixels et en tournant à gauche ou à droite d’un certain angle exprimé en degré. Pour cela, on a besoin de cinq instructions (voir ci-contre) qui sont expliquées et testées avec les élèves. Une fois ce travail rapide de présentation effectué, les élèves se mettent au travail en créant un carré de « 100 » de côté. Ils remarquent sans trop de problèmes que l’on fait 4 fois la même chose, je leur propose donc une nouvelle instruction : la « boucle répéter x fois ». 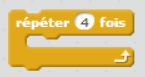 |  |
Deuxième construction : un rectangle
Sans « perdre » leur carré, qu’ils « détachent » de leur algorithme en le laissant dans un coin de leur zone de travail, je leur demande de construire un rectangle de « 200 » de large et de « 100 » de haut, en essayant, tout de suite, d’utiliser un minimum d’instructions.
Cette fois-ci la boucle « répéter 2 fois » sera mise instinctivement en place.
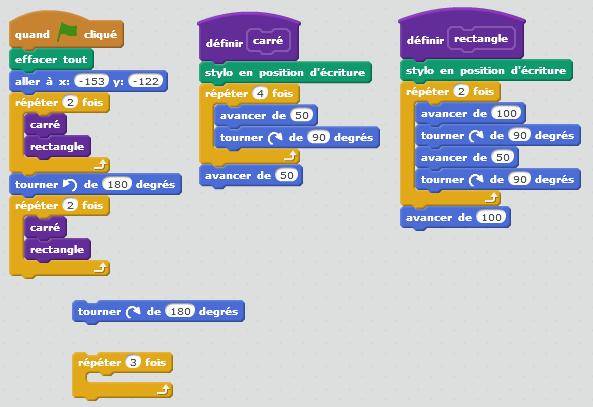
Troisième construction : un mur
Le but du travail étant la construction d’un mur de brique rectangulaire, je leur explique deux choses :
- Pour des questions de solidité du mur, lorsqu’on a fini une couche, on doit poser la couche supérieure en « quinconce ». Pour cela un maçon coupe une brique en deux (d’où l’utilité du carré) avant de poser la brique suivante (entière).
- Informatiquement, les objets « brique » et « demi-brique » ne doivent pas être créés à chaque fois que l’on en a besoin et pour cela, on utilise une instruction de type « bloc ». Je leur montre ce que donnerait un petit programme qui utiliserait ce type d’instruction et qui donnerait le résultat ci-dessous.
L’utilisation des « blocs » permet donc de simplifier l’écriture finale, puisqu’un simple appel à « Carré » ou « Rectangle » suffit, sans que l’on soit obligé de réécrire les instructions.
Un problème rencontré assez fréquemment est la gestion du stylo. Il est souvent préférable que ce soit le bloc qui gère lui-même le stylo (il positionne le stylo en écriture avant de dessiner et le relève une fois terminé).
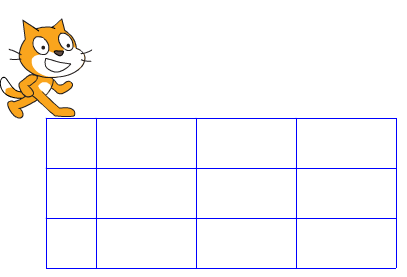
| Quelques élèves parviennent à ce résultat qui répond au problème posé. En étudiant l’algorithme proposé par ces élèves (groupe1), les élèves n’ont pas su remarquer que leur mur aurait pu être construit plus simplement avec une boucle « répéter 3 fois » (le mur est constitué de 3 fois 2 lignes). Du coup, comme le montre l’algorithme ci-contre, c’est un peu long à écrire. En leur posant la question, ils m’expliquent qu’ils ont fait « bouton droit » « dupliqué » et qu’ils ont ajouté 50 au « y » dans le « aller à x:… y :… » : cela ne ressemble-t-il pas à une boucle ?  | 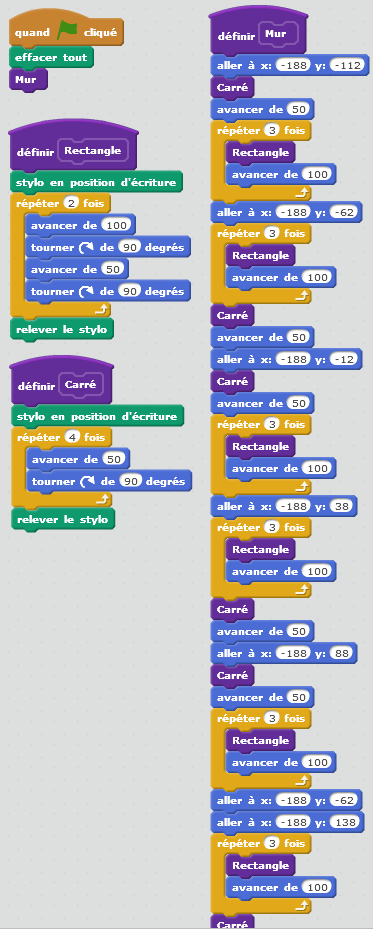 |
Pour d’autres, ils ont bien vu le côté répétitif en ce qui concerne la superposition des lignes, mais obtiennent des résultats moins « solides » du point de vue maçonnerie.

Finalement ceux qui ont vu correctement la répétition des 2 lignes (groupe2 et groupe3) ont choisi de construire de la gauche vers la droite, puis de la droite vers la gauche en « retournant » scratch ce qui était astucieux en soit, mais leur a posé problème pour imbriquer la boucle « répéter 3 fois » car leurs motifs ont été reconstruits sur ceux déjà existants.
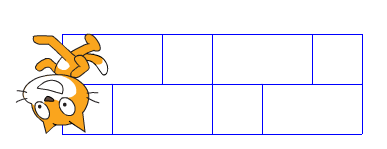
Quatrième construction : un pavage
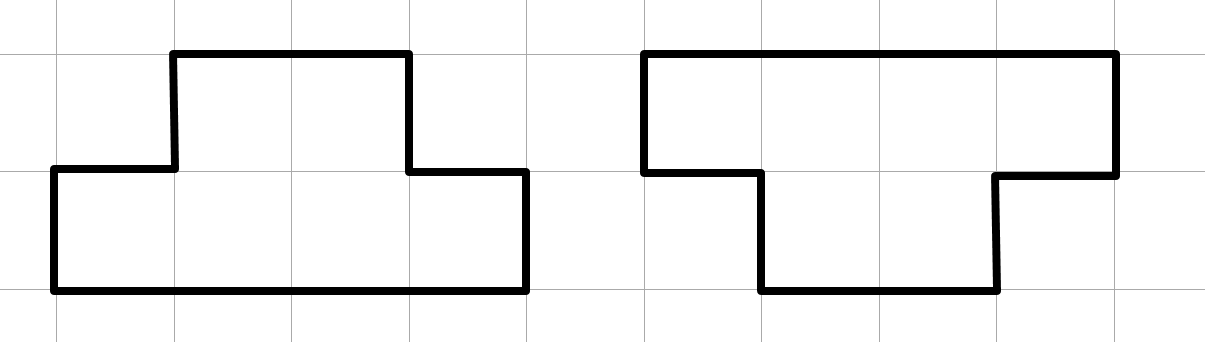 La première heure de construction s’étant bien passée (carré, rectangle et mur), je reviens la semaine suivante en salle multimédia avec les élèves avec pour consigne de réaliser un pavage avec les motifs ci-contre :
La première heure de construction s’étant bien passée (carré, rectangle et mur), je reviens la semaine suivante en salle multimédia avec les élèves avec pour consigne de réaliser un pavage avec les motifs ci-contre :Plusieurs pavages sont alors possibles pour les élèves, à eux de les inventer.
Rapidement, ils se rappellent l’intérêt de créer des blocs.
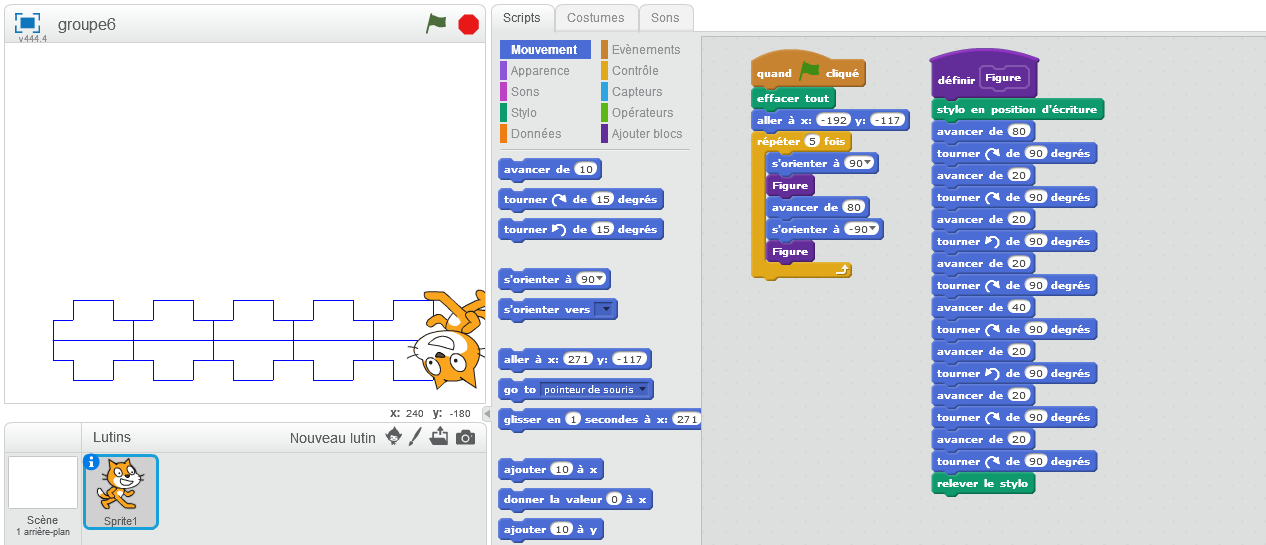
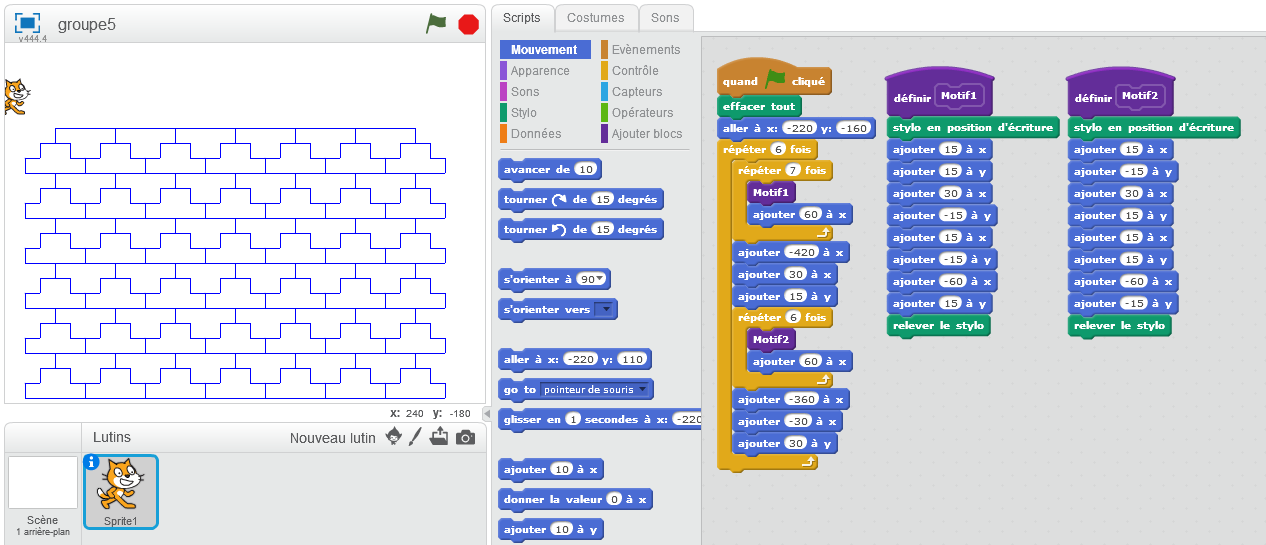
Instinctivement, ils créent deux blocs différents, mais un groupe (groupe6) parvient à comprendre qu’un seul bloc suffit, il faut juste être orienté à 90° ou à -90° pour obtenir une différence dans la visualisation du motif.
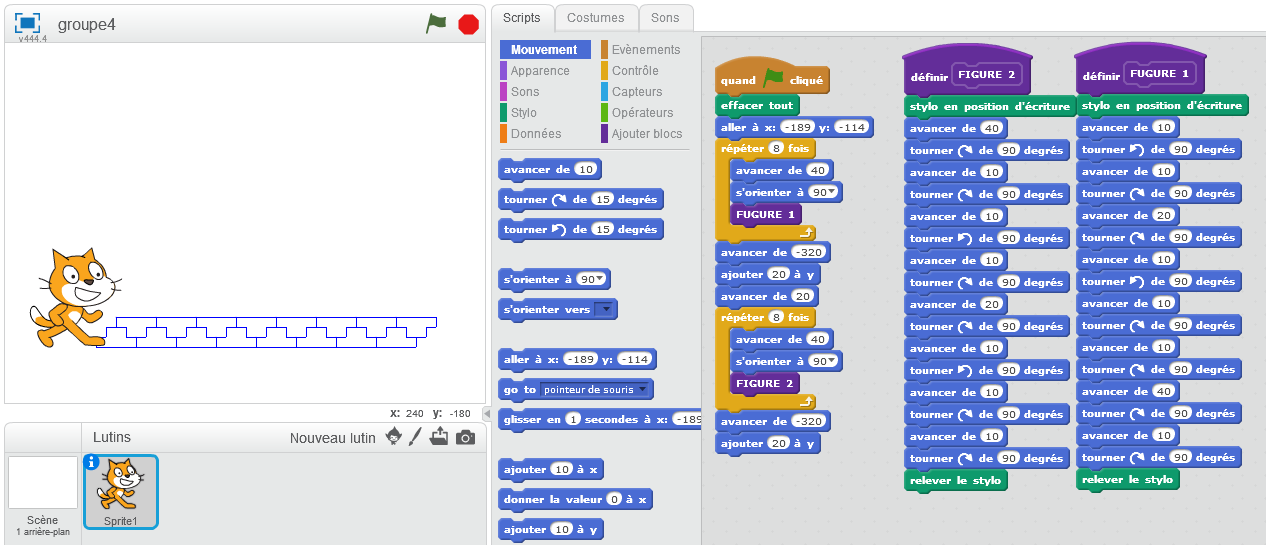
Un groupe (groupe4) arrive au résultat ci-dessous avec 2 lignes de pavage, mais sans finir le reste par manque de temps.
Un autre groupe (groupe5) quant à lui m’avait demandé ce que signifiait « ajouter … à x » et « ajouter … à y » du coup, leur construction de Motif a été simplifiée ainsi que leurs déplacements de ligne en ligne.
Pour aller plus loin
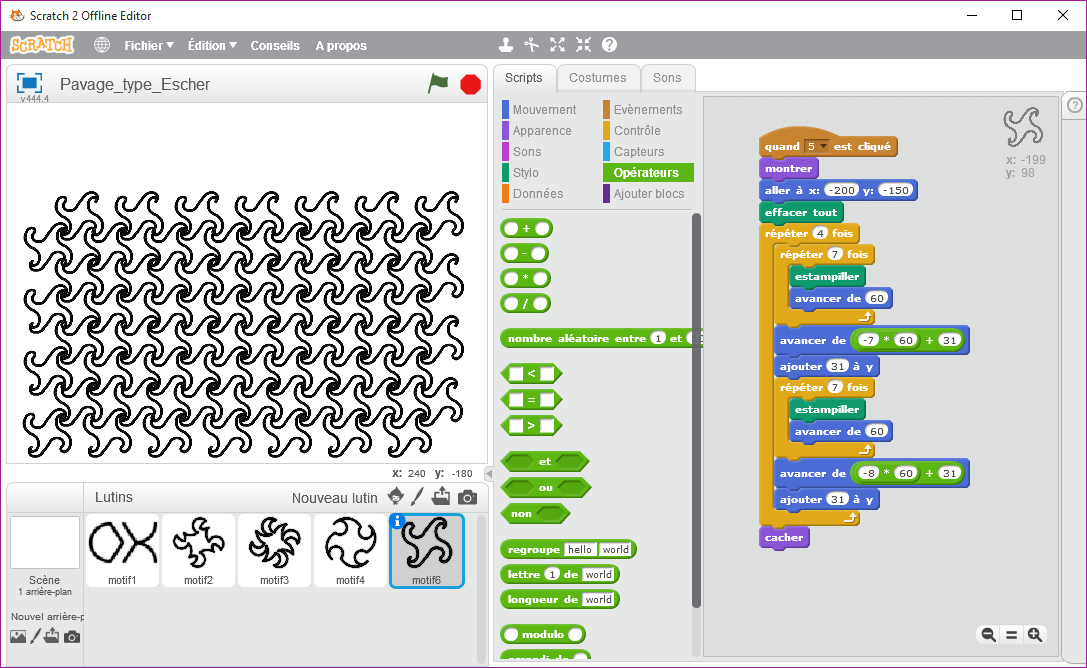
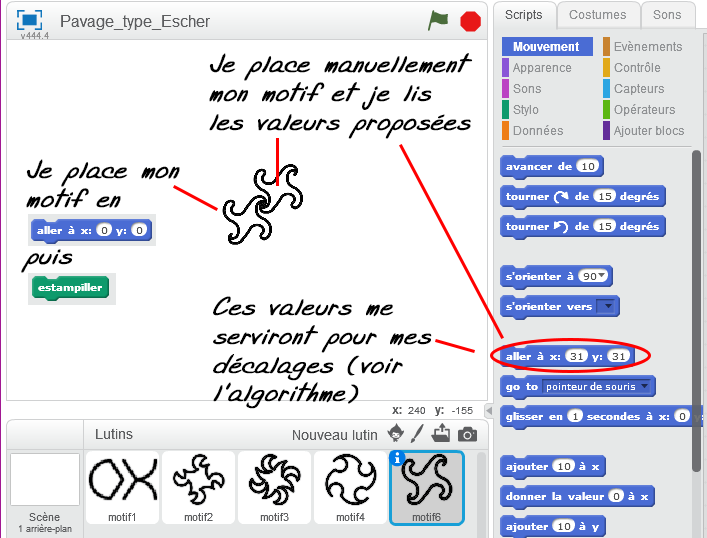
Une séance prochaine, mais non encore réalisée (peut-être avec 2 mois de décalage) j’ai envisagé de prendre un motif, non pas dessiné comme dans le paragraphe précédent, mais de type image (Lutin) et de réaliser un tel pavage comme l’aurai fait Escher (artiste néerlandais 1898-1972).
Pour cela, il suffit d’ « estampiller » le motif avec la commande :

Voici ce que cela pourrait donner, en sachant que les 4 premiers sont simples à mettre en place contrairement au cinquième qui demande à tester des valeurs au préalable.
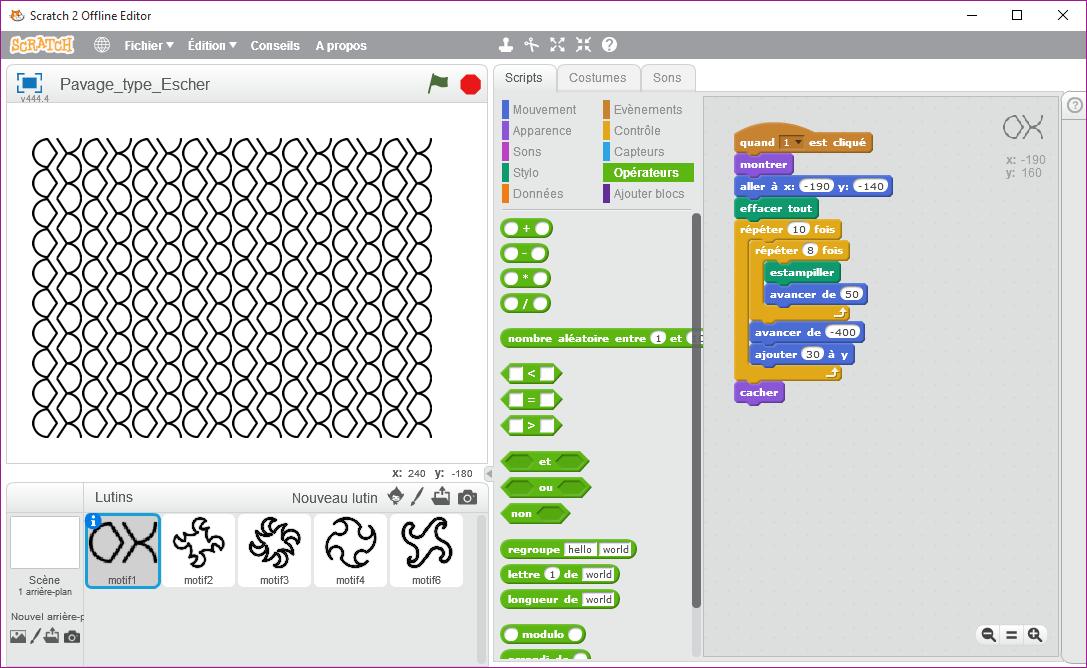
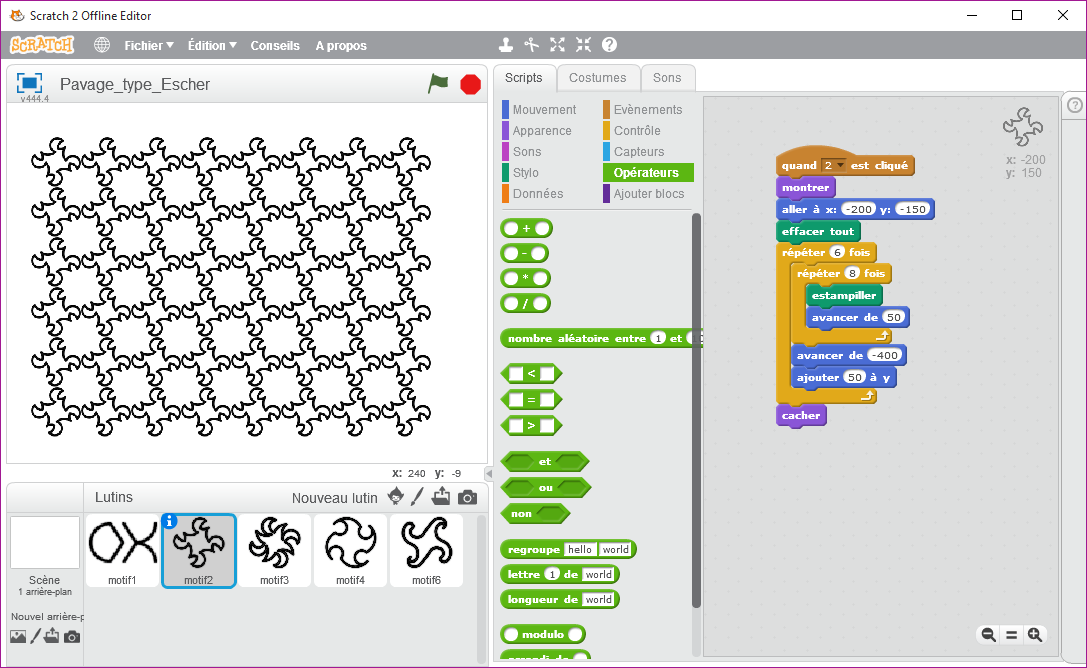
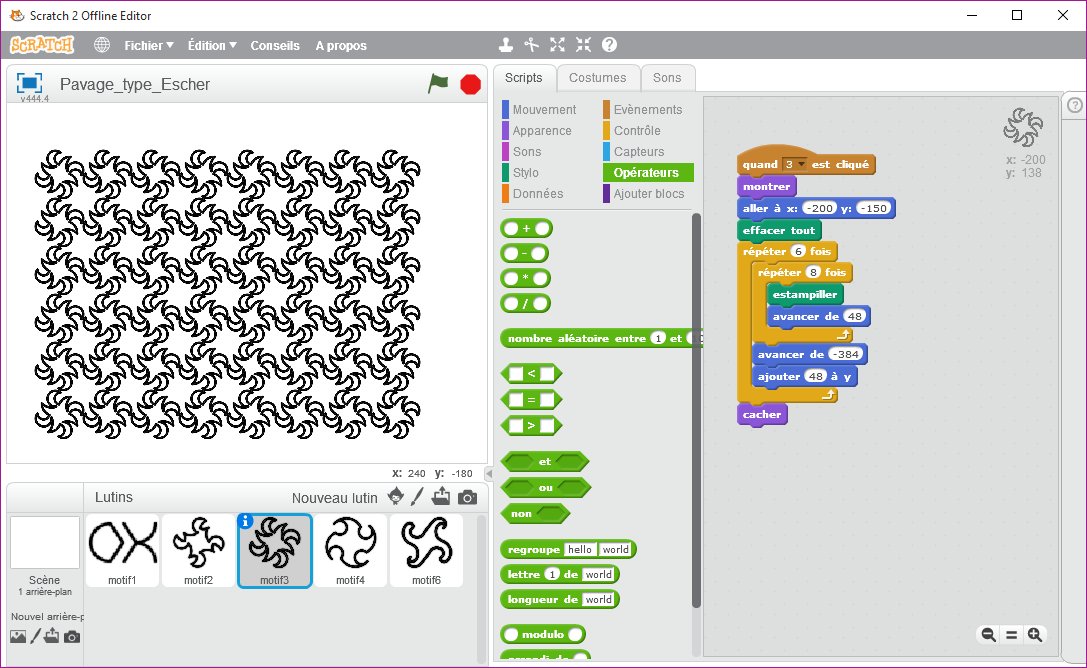
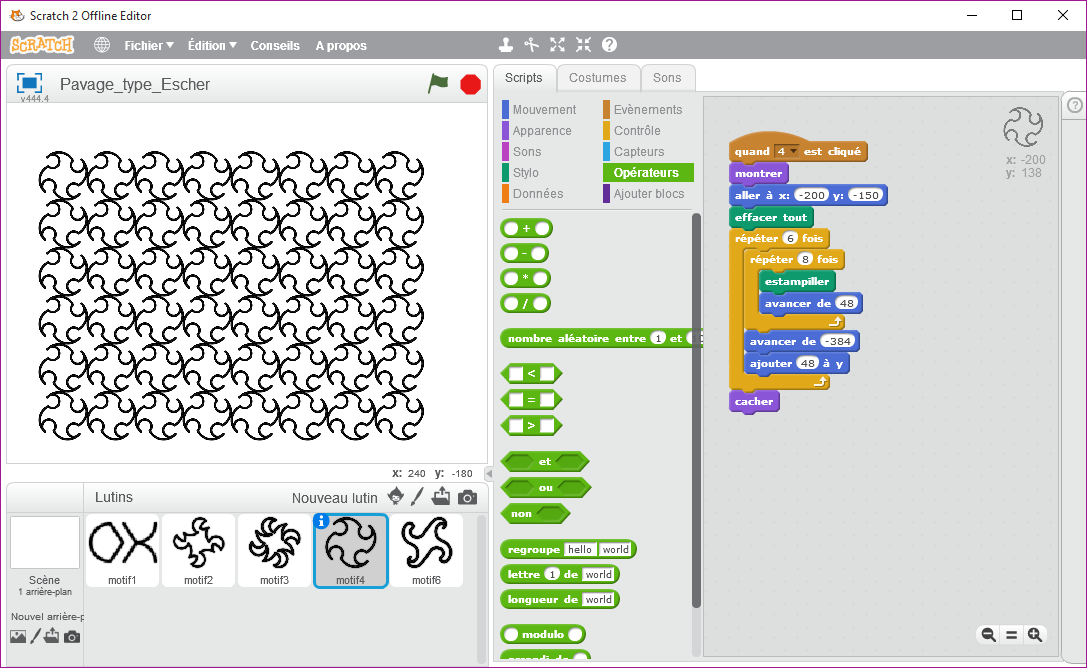
Emmanuel malgras, Enseignant au Collège Pierre et Marie Curie - le pellerin (44)
information(s) pédagogique(s)
niveau : tous niveaux, Collèges tous niveaux, 4ème, 3ème
type pédagogique :
public visé : non précisé, élève, enseignant
contexte d'usage : salle multimedia
référence aux programmes :
ressource(s) principale(s)
|
|
la ruche | 08/01/2018 |
| Un pavage sous forme de ruche : un défi pour l'agorithmique. | ||
| algorithmique, pavage, scratch | Emmanuel Malgras | |
documents complémentaires
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA