mathématiques

Mise en place des cartes.
En 2h en salle multimédia (2 élèves par ordinateur), ils ont tous réussi à placer les cartes ou l’objet à trouver de manière aléatoire. Voici 4 stratégies déployées par les élèves :
Stratégie 1 
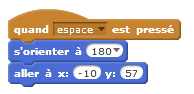
Les élèves décident de placer une carte de manière aléatoire entre les trois positions, puis placent la 2ème et la 3ème carte au deux places restantes. L’objet à découvrir est toujours sous la carte 1.
Stratégie 2 
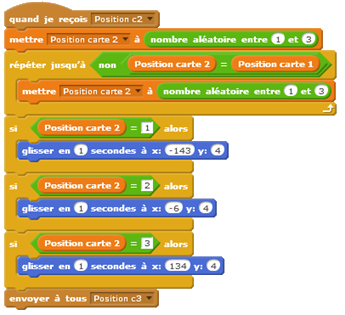
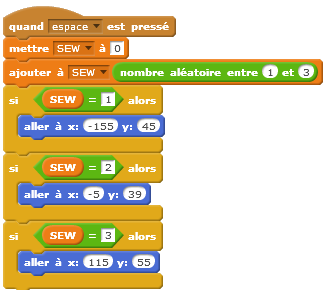
Les élèves décident de placer une carte de manière aléatoire entre les trois positions, puis placent aussi la 2ème carte de manière aléatoire en vérifiant qu’elle n’est pas à la position de la 1ère carte, et enfin font de la même manière pour la 3ème carte. Là encore l’objet à découvrir est toujours sous la carte 1.
Stratégie 3 
Les élèves décident de placer les cartes toujours au même endroit, mais déplacent l’objet caché.
Stratégie 4 
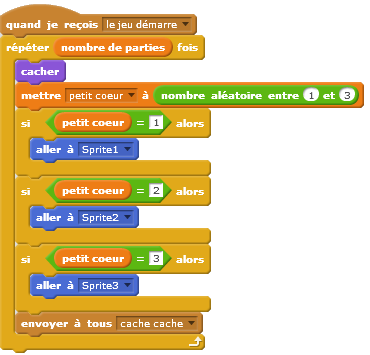
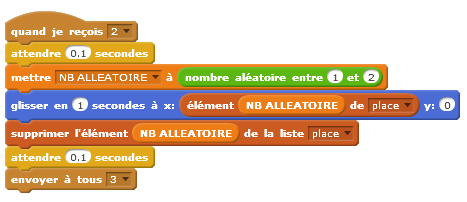
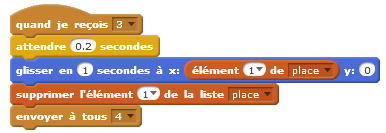
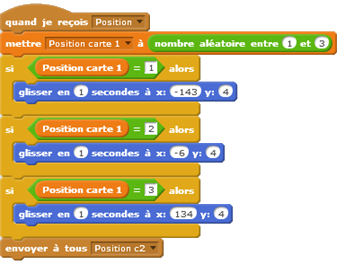
Les élèves utilisent une liste pour placer les cartes de manière aléatoire. L’objet à trouver est toujours sous la carte 1.
 
Fin du jeu :
Une bonne moitié des élèves a pu aussi programmer la version de base du jeu : on choisit une carte et le programme nous dit si on a gagné ou pas.

Quand l’objet est toujours sous la même cartes (par exemple la carte 1)   

Le lutin cherché est « apple » et l’on clique sur une carte.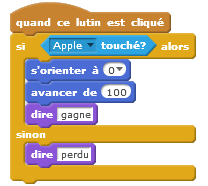
Le lutin cherché est « key » et l’on clique sur une carte.	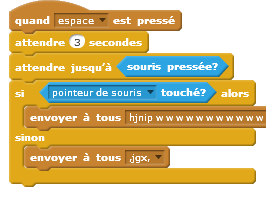Voici un des messages envoyés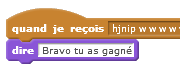
La position de l’objet recherché est stockée dans la variable « position 1 »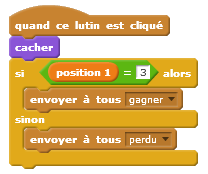

Quand l’objet est toujours sous la carte 1 et que ce sont les cartes qui sont placées de manière aléatoire :
 

Selon que c’est le bon lutin ou non qui est choisi.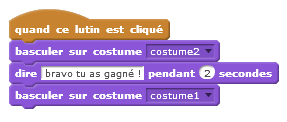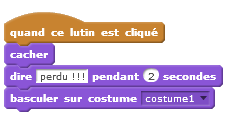

 
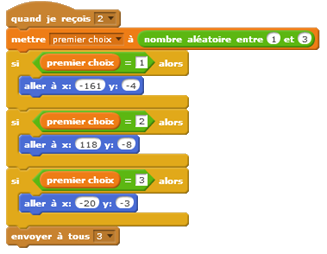
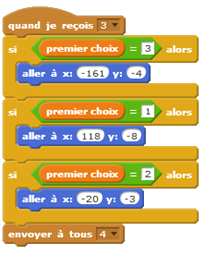
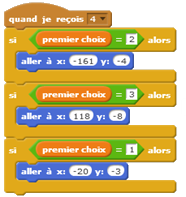
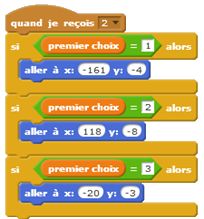
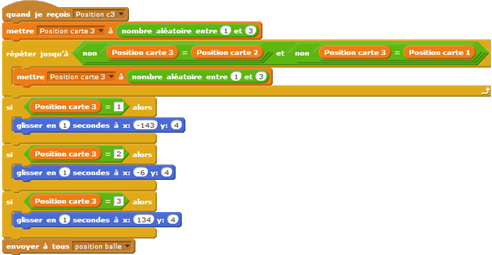
Deux groupes ont réussi à programmer la variante du jeu, qui consiste à retourner une des deux cartes non choisies (qui n’est pas celle derrière laquelle se cache l’objet) et de demander à l’utilisateur s’il souhaite changer ou conserver son choix.

Les élèves ont pu tester le programme avec variante et se sont rendu compte qu’il était préférable de changer de choix. Une étude probabiliste a été faite en classe, avec la construction d’un arbre, pour prouver cette conjecture.

 
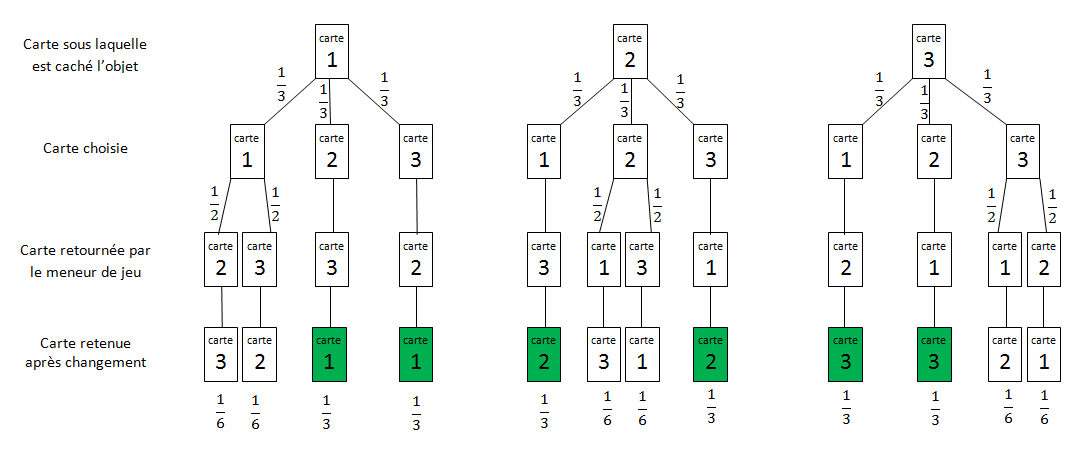
Les élèves ont conclu que quelle que soit la carte sous laquelle l’objet était caché, on a 2 chances sur 3 de gagner si on change.


Il y a eu un 2ème type de raisonnement beaucoup plus efficace :

• Si on choisit la carte qui cache l’objet, une des 2 cartes perdantes sera retournée et quand on changera, on choisira l’autre carte perdante. 
• Si on choisit une des cartes perdantes au début, l’autre carte perdante sera retournée et quand on changera notre choix on aura la carte gagnante.

Donc si on commence par choisir une carte perdante (soit une probabilité de 2/3), et que l’on change notre choix, on est sûr de gagner ; par contre si on choisit la carte gagnante au départ (soit une probabilité de 1/3), on est sûr de perdre.


Fichiers joints
Les fichiers élèves ne sont pas forcément aboutis mais ils sont le fruit d’un travail réalisé en 2h en salle multimédia.