mathématiques

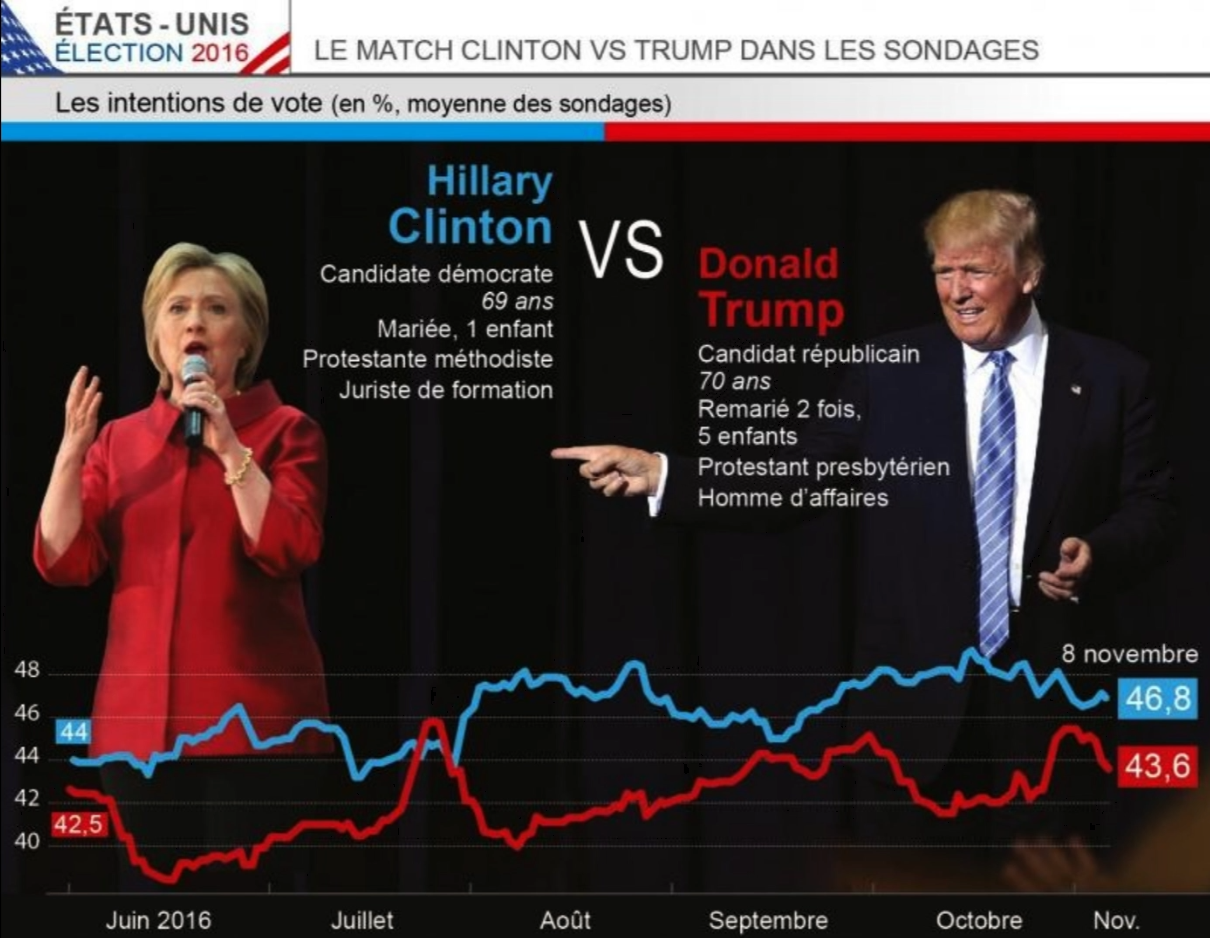
Pour les besoins de cette activité, plusieurs préambules sont nécessaires. En effet, ils n’ont a priori que peu de connaissances sur le tableur, tout comme sur les différents modes de scrutin.

J’ai fait le choix personnel de commencer par une activité en classe entière de l’utilisation d’un tableur sur un conseil de classe (fictif) d’une classe de 3e.
Un fichier tableur de présentation sera projeté au tableau et j’attends des propositions de formules pour le compléter “en live”. Les élèves ont à leur disposition le même fichier que celui projeté mais en version papier avec des cadres “commentaires”, qu’ils complèteront une fois la formule validée. L’utilisation d’un TBI ou TNI est préférable, mais pas indispensable.
Les objectifs de cette séance (d’une durée d’environ 1 heure sont les suivants) :

• Réactiver les méthodes d’utilisation du tableur (fonctions simples) :
  • Utilité du symbole =
  • Différence entre : et ;
  • Calculs simples + - * / (pour pouvoir calculer une quatrième proportionnelle)
  • Moyenne()
  • Arrondi() avec le nombre de décimales choisi
• Découvrir de “nouvelles fonctions” utiles pour l’activité et savoir où aller les chercher si besoin avec l’aide intuitive du logiciel :
  • Si.Conditions()
  • $ colonnes $ lignes

La présentation de la vidéo est là pour leur remémorer que Donald Trump a été élu en 2016. Ils semblent être au courant, mais je voulais en être sûr donc leur ai au préalable demandé s’ils savaient :

• Qui était le président américain actuel ?
• Qui était le précédent ?
• Quel était le candidat rival de Donald Trump en 2016 ? (moins de certitudes chez eux)

Après ces deux questions préalables, je leur ai fait visionner la vidéo.
S’ensuit une discussion sur l’universalité du scrutin, puis une discussion autour du modèle américain, qui sera précisé dans l’activité suivante.

ELECTIONS PRESIDENTIELLES FINALISEE (vidéo)

N’ayant pas pu être épaulé par mes collègues d’Histoire-Géographie-EMC (par manque de temps), j’ai créé une activité présentant la différence des modes de scrutin. Celle-ci est constituée d’un document A4 paysage ou seule la page de gauche est à compléter (à l’oral avec les élèves), la page de droite étant un mémo pour la suite de l’activité.
Les deux activités conjointes des paragraphes b. et c. ont duré 1 heure environ car ils avaient (pour les deux classes) beaucoup de questions (par exemple, pourquoi certains Etats avaient plus de Grands Electeurs que d’autres …)
Le bilan est assez positif, car bon nombre d’élèves prennent conscience que le travail mathématiques va être concret, et le questionnement lié à leur âge les concerne.

Cette activité tableur correspond à l’aboutissement du thème travaillé, et doit permettre de répondre à la problématique encadrée en première page. Elle était sensée durer une heure, mais il s’avère que très peu d’élèves ont réussi à la terminer sur ce temps imparti. Au vu de l’intérêt des élèves pour l’activité, j’ai donc décidé de la prolonger d’une demi-heure, et de terminer le travail en classe entière pour celles et ceux qui n’avaient pas encore terminé.

Les objectifs de l’activité sont les suivants

• Exercer son esprit critique pour envisager les informations nécessaires pour répondre à une question
  • Demander les informations
  • Vérifier que cette quantité d’informations est suffisante
• Utiliser des calculs de pourcentages sur tableur
  • Utiliser la numérotation des cellules
  • Calculer avec « = », « * », « / », « + », « - »
  • Différencier « ; » et « : »
• Utiliser les fonctions précédentes dans le cadre d’un tableur complexe
  • SOMME()
  • MOYENNE()
  • ARRONDI()
  • SI.CONDITIONS()
• Conclure en utilisant un raisonnement conjoint (expliciter son raisonnement)

Le matériel que j’ai utilisé (en salle informatique et en demi-groupe) pour la séance est le suivant

• Casques (écouteurs possibles)
  • L’objectif est qu’ils puissent communiquer avec moi sans que les autres membres du groupe n’entendent notre conversation
• Logiciel de prise en main des ordinateurs des élèves à distance (pour moi “VEYON”)
  • Cela m’a permis de donner un fichier incomplet aux élèves
  • En effet, il leur manque plusieurs informations dans le fichier donné pour répondre à la problématique
  • Ils doivent donc communiquer avec moi lorsqu’ils ont trouvé quelle(s) information(s) manquait(ent)
  • Lorsqu’ils me demandaient une information pertinente, je leur transmettais le fichier correspondant par le logiciel en question.

La mise en place de l’activité a été la suivante

• Je leur présente le fichier tableur “monstre” auquel ils vont être confronté en dézoomant volontairement pour qu’ils voient à quel point il est conséquent. Mon objectif est de les amener à penser que se passer de tableur et faire les calculs “à la main” est illusoire, mais sans le leur dire.
• Je leur précise que le fichier est volontairement incomplet et qu’il faudra qu’ils me demandent des informations pertinentes sur ce qu’il leur manque pour que je les leur transmette.
• Je leur précise où trouver le fichier sur le réseau pédagogique du collège.
• Je les laisse s’installer à leur place devant un ordinateur et leur précise que je ne répondrais à aucune question, hormis par casque et les laisse en autonomie.
• Précision : ils ont bien évidemment droit à l’aide-mémoire des activités précédentes.
• Les élèves s’imprègnent du fichier tableur (certes lourd à prendre en main, mais le but est là !)

L’activité s’est déroulée comme je le pensais

• Des élèves voient instantanément les informations nécessaires et suffisantes : le matériel mis en place leur a permis d’avancer à leur rythme.
• D’autres ne voient pas tout de suite mais poursuivent leurs investigations et finissent par trouver des idées.
• D’autres commencent à abandonner mais la vision prof des différents ordinateurs permet de le voir et on peut communiquer avec eux pour les aider.
• Un élément judicieux est néanmoins apparu et m’a été relaté au casque par plusieurs élèves : l’inutilité de certaines données (les candidats ayant très peu de voix). J’ai à ce moment arrêté tout le monde et leur ai montré au tableau une manipulation permettant de les cacher. L’activité a alors repris.

Bilan (au bout d’une heure d’activité)

• Aucun élève n’est arrivé au bout de l’activité par manque de temps, mais l’ensemble à trouver au moins une idée de ce qui pouvait manquer.
• Je leur demande d’enregistrer leur travail avec leur nom et prénom.
• Je compte terminer cela en binôme à la séance suivante (car classe entière)

Fin de l’activité

• J’ai choisi de constitué les binômes avec des élèves qui avaient demandé au moins une des informations nécessaires, mais différentes. Les élèves qui avaient demandé toutes les informations nécessaires à la séance précédente ont été mis ensemble.
• Je les ai laissé en autonomie, mais en me déplaçant cette fois dans la classe pour les aider “individuellement”
• A la fin de la séance (que j’ai volontairement raccourcie à une demi-heure pour faire un bilan en plénière), une grosse moitié de la classe avait terminé le travail.
• Nous en avons fait une correction au tableau avec un fichier récupéré qui était complet.

Etant donné la taille des fichiers, je privilégie de vous donner un lien de deux binômes étant arrivé au bout sans aide. Dans le deuxième fichier en lien, on remarque que les élèves ont commencé à faire le travail à la main, puis, par “ras-le-bol” assez significatif, ont réfléchi à utiliser une formule.
 

Pour les élèves

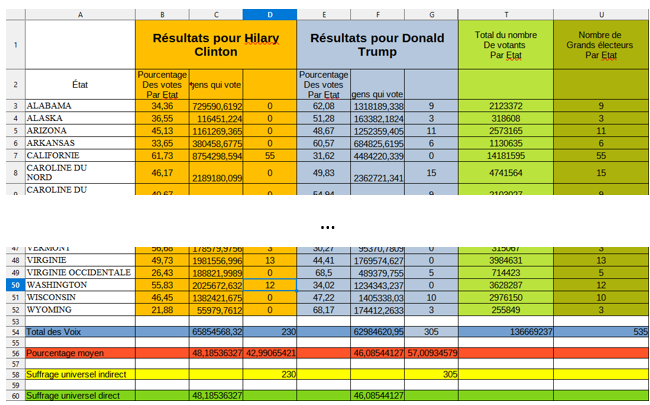
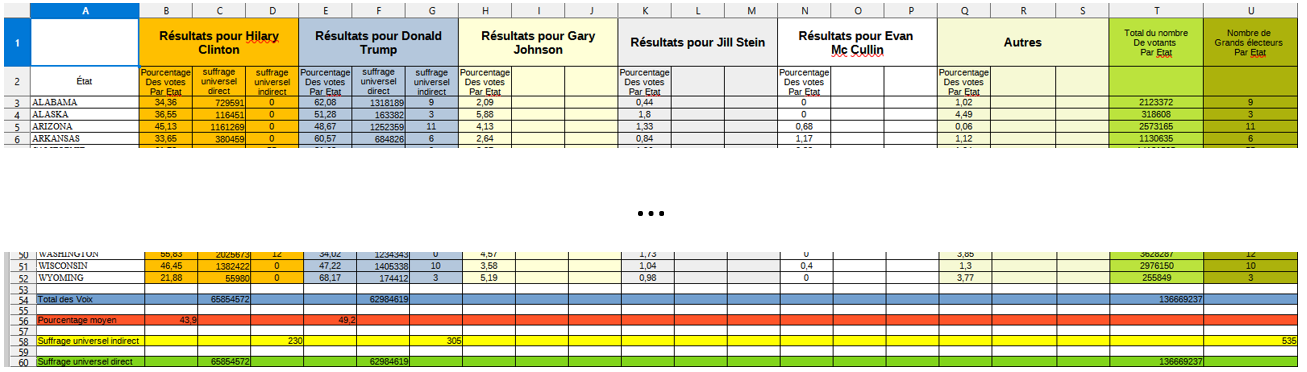
Le bilan est très positif. Les deux classes se sont réellement investies, et ont réellement progressé sur l’utilisation du tableur. Ils voient notamment les intérêts de l’usage d’un tel outil, et sont, pour une partie non négligeable, autonomes (ou presque) sur son usage, et ont travaillé avec un réel engouement.
Nombre d’élèves “en froid” avec les mathématiques y ont trouvé un intérêt, et se sont investis bien plus qu’à l’accoutumée.
Le questionnement relatif à la situation les a également amené à réfléchir sur les modes de scrutin, et à réaliser que les mathématiques sont omniprésentes.

Pour l’enseignant

Bilan très positif également, les élèves ayant réellement progressé, et ayant été très motivés par l’activité. En revanche, l’activité est difficile à mettre en place et prend du temps. D’autre part, il est nécessaire d’organiser les séances avec grand soin quant au “timing”, et impose d’avoir des groupes classes ainsi qu’un matériel informatique suffisant.
Certaines questions (pertinentes sur les modes de scrutins), auxquelles je ne m’attendais pas forcément et sur lesquelles je ne suis pas expert m’ont été posées, et sont restées sans réponses pendant la séance. Il est surement préférable de se renseigner au préalable de façon très détaillée sur le modèle américain pour les anticiper.

Comme il est précisé dans le fichier lié à l’activité “PRESENTATION DU MODE DE SCRUTIN AMERICAIN”, plus précisément dans “LE FICHIER ELEVES A COMPLETER”, la règle du scrutin américain y est ici simplifiée.

En effet, la règle du “WINNER TAKES ALL” n’est pas appliquée dans deux Etats : dans le Maine et dans le Nebraska ; le nombre de Grands Electeurs obtenus pour chaque candidat s’établit à la proportionnelle (pas de changement de résultat pour l’activité bien évidemment !).
On pourrait donc proposer aux élèves d’affiner le résultat obtenu.

Une autre piste serait de comparer ainsi d’autres modes de scrutins ou de demander à des élèves vraiment très efficaces de faire des recherches internet sur les modes de scrutins existants, et de les comparer en EMC.