mathématiques

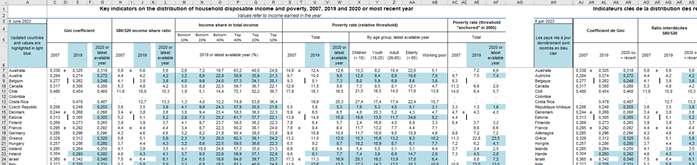
Dans les programmes, le thème « répartition des richesses » est introduit par la phrase suivante : « l’étude de la répartition de richesses dans la population d’un pays, des salaires dans une entreprise, etc., et la comparaison des différentes répartitions sont des occasions de réinvestir des connaissances antérieures de statistique descriptive et de construire de nouveaux outils d’analyse faisant intervenir les fonctions d’une variable (notamment des fonctions de répartition) et le calcul intégral ». L’une des difficultés est donc de trouver des données exploitables. Après discussion avec quelques collègues de SES, certains sites ont été indiqués. La difficulté reste de trouver des données brutes compréhensibles pour un professeur de mathématiques. L’un des sites possibles est le site de l'Organisation de coopération et de développement économiques (OCDE ou OECD en anglais). Il permet d’avoir accès à des statistiques sur plusieurs pays et aux data base. Celle trouvée se présente comme ceci :

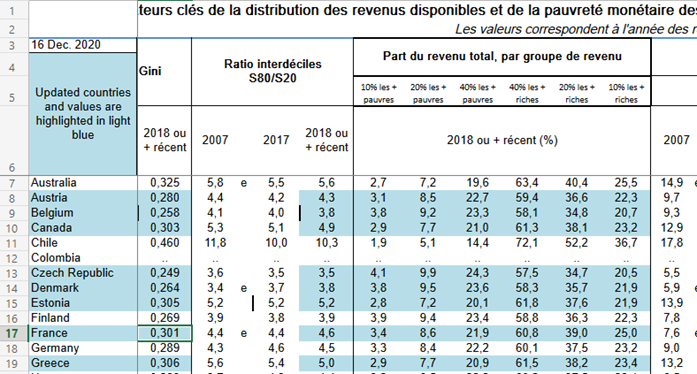
Et en zoomant :

Elle est relativement compliquée à lire pour quelqu’un d’aussi peu expérimenté que moi. Après réflexion, je décide d’interpréter certaines données et de les proposer sous un autre format.
 

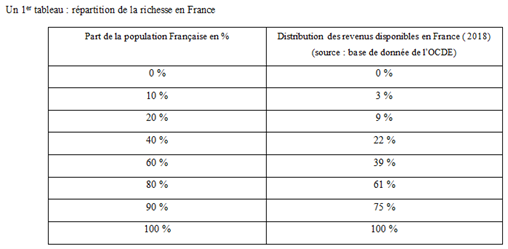
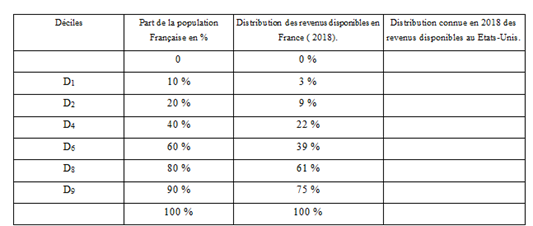
Les données qui m’intéressent sont celles qui proposent certains déciles pour l’année 2018 : 10%, 20%, 40% les plus pauvres puis 40%, 20%, 10% les plus riches. Dans un premier temps, j’ajuste ces données pour les faire correspondre à une vision plus classique en France. La source est indiquée mais les valeurs sont arrondies à 0.01 près :

Ce premier travail facilite la compréhension, notamment pour les élèves n’ayant pas la spécialité SES.
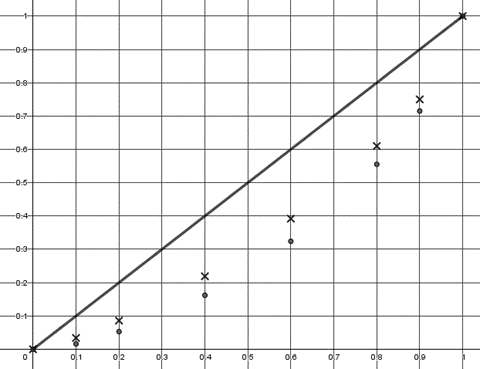
Plusieurs questions sont posées, un graphique est demandé et la 1ère bissectrice est tracée. Cette première activité se termine sur la question : comment interpréter cette droite d’équation y=x dans le contexte de l’exercice ? (Réponse : elle indique une répartition des richesses strictement égalitaire.)

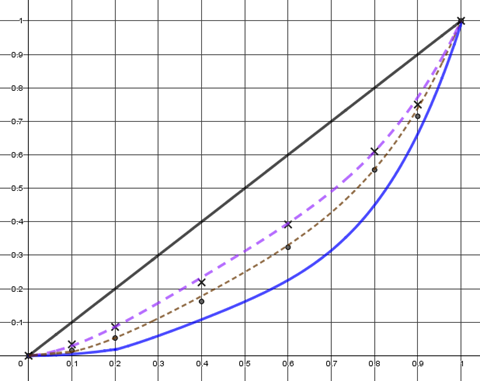
Il s’agit de comparer la répartition des richesses aux Etats-Unis et en France. Un nouveau graphique est proposé. C’est une satisfaction de constater que ce graphique est proche de celui indiqué par les élèves. On retrouve les données de la France (points en forme de croix). Des points correspondant aux données pour les États-Unis sont rajoutés.

Un tableau complète ce graphique. Il est fourni afin de parvenir plus vite au cœur du nouveau problème.

L’objectif est de faire intervenir de nouveaux outils mathématiques pour le traitement. Il est alors demandé de proposer une courbe passant par tous les points afin de déterminer d’autres valeurs. Certains élèves se rappellent que de telles courbes sont des courbes de Lorenz (ceux en spécialité SES).
La courbe tracée à partir des points correspondants à la France, nous réfléchissons collectivement aux propriétés de la fonction associée à cette courbe. Ce travail permet de retrouver la notion de continuité et la notion de convexité.
Le logiciel geogebra est alors fortement exploitée par le professeur pour déterminer une fonction polynomiale possible (ce qui est plus pratique pour le calcul d’aire sous la courbe – voir partie 3). Ce travail permet de reparler du thème « modèle défini par une fonction d’une variable ». Il s’agit de savoir si la fonction proposée répond bien aux propriétés trouvées à savoir :
l’image de 0 est 0,
l’image de 1 est 1,
la fonction est continue sur [0 ; 1],
la fonction est convexe sur [0 ; 1].
Il est à signaler que cette dernière notion n’avait pas été introduite la deuxième année. C’est donc cette activité qui a véritablement permis de travailler ce concept en maths complémentaires puisqu’un exemple concret était obtenu : une courbe de Lorenz ne peut pas être la courbe représentative d’une fonction non convexe sur [0 ; 1]. Outre la propriété des fonctions convexes via la position des tangentes par rapport à la courbe de la fonction, ce travail a été prolongé par la mise en place de la propriété liant le signe de la dérivée seconde et la convexité de la fonction, l. ()

Les données obtenues sur le site de l’OCDE donnent un nouvel indicateur utilisé en économie à savoir le coefficient de Gini qui est un indicateur synthétique permettant de rendre compte du niveau d'inégalité pour une variable et sur une population donnée. La dernière partie explique donc comment calculer ce coefficient et donc de retrouver l’indicateur (ou une valeur proche suivant la fonction retenue lors de l’approximation.

Pour cette partie, un nouveau pays est introduit ainsi que de nouvelles propositions de fonctions répondant aux 4 critères trouvées dans la partie 2. Certaines de ces fonctions sont définies par morceaux et donc non dérivables en tout point de [0 ;1] (la propriété est alors admise à partir du graphique – aucun élève n’est revenu à la définition d’une fonction convexe). Ce travail permet de revenir sur le calcul intégral (et donc le thème « calcul d’aires ») et, pour certains, d’avoir un exemple concret pour utiliser certaines propriétés du calcul intégral telles que la relation de Chasles.

L’exemple proposé est un exemple d’exploitation de données brutes en mathématiques. Pour le professeur, cela demande du temps de recherche, du temps de compréhension et du temps pour construire un problème global cohérent. Néanmoins, cela a permis d’introduire parfois certaines notions (convexité), ou d’améliorer la compréhension d’autres (continuité, calcul intégral). Pour les élèves, ceux ayant choisi la spécialité SES, cela a permis de créer une bonne passerelle entre les deux matières et donc de mieux comprendre certains indicateurs statistiques utilisés en économie (calculs des indices de Gini de la France, des Etats Unis et éventuellement de la Chine). La grande majorité des élèves a trouvé la situation motivante et a pu aller à son rythme (différenciation possible en ajoutant des pays). La question reste posée quant à l’éventualité de proposer les données brutes et de demander aux élèves de les exploiter (activité 1).