mathématiques

2. À votre avis !

Cette phase consistait à établir les connaissances des élèves sur différentes grandeurs telles que des tailles, des vitesses, des masses…


Les réponses ont été données sous forme de sondage à main levée. Cette première phase a été proposée pour une mise en train. Le but n’était pas encore de prendre et de justifier sa réponse, mais plutôt de prendre l’habitude de proposer des réponses sans avoir peur du regard des autres.

3. Des calculs à analyser

Consigne donnée aux élèves : parmi les 3 calculs ci-dessous, 1 seul est faux. À votre avis, lequel ?

Voici quelques exemples de questions posées (les thèmes « ordres de grandeur », « partie décimale », n’étant bien évidemment pas annoncés aux élèves).

Première série : questions sur les ordres de grandeur

Pour vraiment parler d’ordre de grandeur, le dernier chiffre doit être convenable, seules les unités ou les dizaines doivent varier dans la réponse.
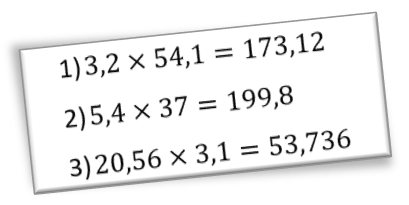
Je choisis de volontairement diminuer la dizaine de la troisième question pour que l’ordre de grandeur soit facilement repérable.
Argumentation entendue : 20,56×3,1 doit être plus grand que 20×3=60
Des retours

• Beaucoup d’élèves constatent effectivement que pour le troisième calcul le résultat doit être forcément plus grand que 20×3=60.
• Plus étonnant : certains annoncent que « C’est le 1), car 3×50=150, et c’est le plus loin de la réponse ». Ils comparent les écarts entre ordre de grandeur et la réponse.
   

Deuxième série : questions sur les ordres de grandeur

Comme précédemment, le dernier chiffre doit être convenable. Ici, on a une proposition qui est vraiment très loin de la réponse exacte.
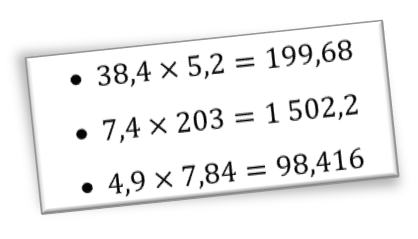
Argumentation entendue : l’ordre de grandeur pour le troisième calcul est vraiment très différent de la proposition de réponse.
Des retours

• Une partie des élèves trouve la réponse, mais ils sont moins nombreux que pour la première série.
• Plus étonnant : c’est le deuxième calcul, car le résultat n’est pas dans les centaines.
   

Troisième série : problème dans la partie décimale

Ici, le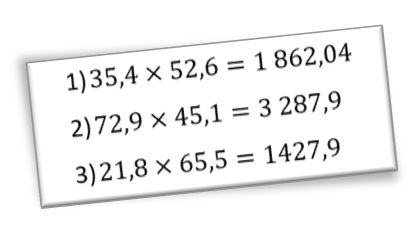 nombre de chiffres pour la partie décimale doit toujours être de 2 chiffres : des dixièmes multipliés par des dixièmes donnent des centièmes.
Argumentation entendue : tous les calculs doivent avoir 2 chiffres après la virgule et comme un seul calcul est faux, c’est forcément le deuxième qui doit se terminer par 9 (centièmes) car le troisième calcul doit se terminer par un 0, mais on peut ne pas l’écrire (21,8×65,5=1 427,90).
Des retours

• C’est le premier, car il a 2 chiffres après la virgule
• C’est le troisième, car il manque un espace entre les centaines et les milliers (erreur d’écriture de ma part qui a semé le doute dans la tête de certains élèves).
• C’est le troisième, car 8×5=40, ça doit se terminer par 0 et ça se termine par 9
• Très peu d’élèves trouvent la bonne réponse (aucun dans certaines classes).
   

4. Des unités manquantes

Saurions-nous capables de retrouver l’unité ? Peut-être pas ! Le but était plutôt de ne pas donner d’unité improbable !
Voici deux exemples proposés aux élèves :
             
Le réflexe de la grande majorité des élèves consiste à éliminer les unités pas possibles : si c’était des secondes, même eux y arriveraient et pour les heures c’est impossible : c’est donc des minutes !
Le débat a continué sur 24 minutes, est-ce possible ? Comment vérifier cette information ? Ils ont plein d’idées et franchement de bonnes idées (sites officiels des fédérations sportives, sites officiels des records, sites des journaux…).


                

La réponse est 11,2 km/s (soit plus de 40 000 km/h). L’unité proposée ici des km/s est peu commun et le but n’était pas de la trouver, mais plutôt d’en éviter certaines comme les km/h ce qui a été le cas. Différentes autres propositions sont proposées, comme des km/min et des mach.

5. Des énigmes

Consigne pour cette énigme, la calculatrice n’est pas autorisée…

Les explications des élèves ne sont pas toujours simples !

Heureusement que ce sont les élèves qui expliquent aux élèves…

Tout le monde n’y arrive pas, mais les élèves qui ont compris parviennent à bien expliquer et à persuader les autres.

Si les trois premiers thèmes semblent plus adaptés aux mathématiques, il me semble que le quatrième l'est également, car il a obligé certains élèves à se poser des questions sur les énoncés : qu'est-ce qui dans l'énoncé me pose problème et m'empêche de trouver la solution, qu'est-ce qui dans l'énoncé me fait répondre trop vite ?

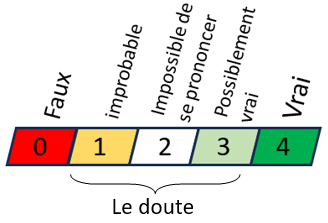
6. Thème pour les 4e : avec un indice de certitude

Sur différentes notions, on peut leur poser des questions simples avec un indice de confiance pour une proposition donnée. L’indice de confiance que j’ai choisi va de 0 à 5.

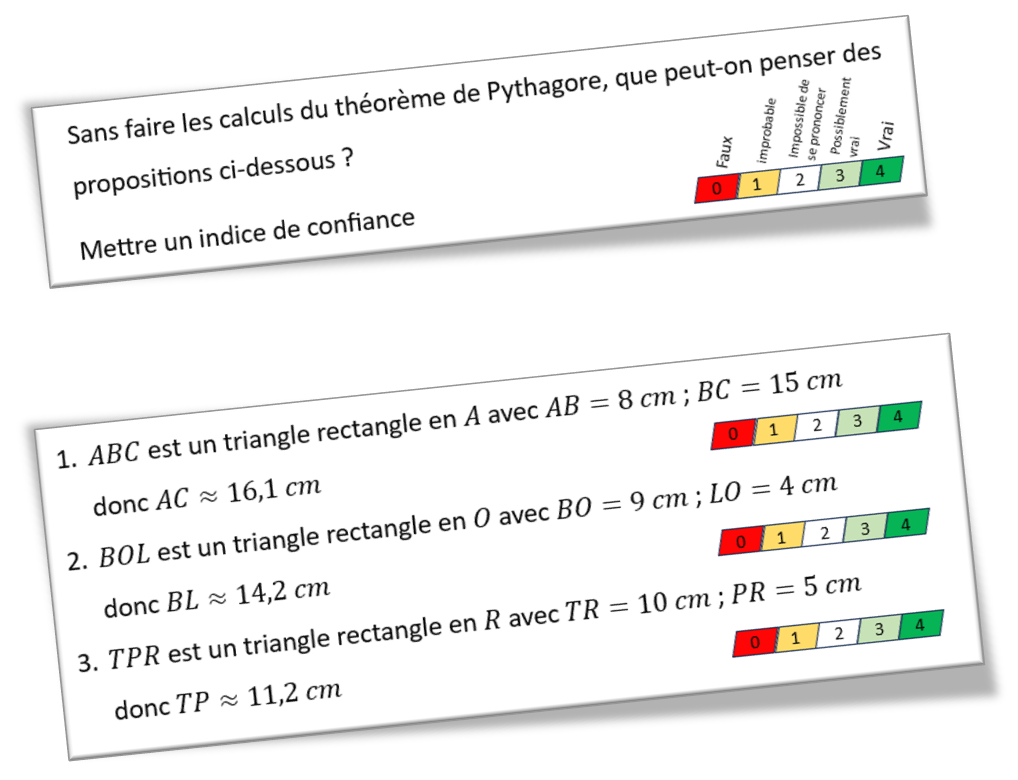
Voici, ci-dessous, un exemple avec 3 propositions liées au théorème de Pythagore que j’ai proposé sur 3 débuts d’heure.
Dans ce type d’activité, il est évident pour nous, mais pas pour les élèves que pour avoir un indice de confiance de 4, ils doivent effectuer les calculs qui montreront si le résultat est juste ou non.
Certains finissent par le comprendre et comme ils ne doivent pas faire les calculs, ils se positionnent sur le 3 au maximum.

• Pour le 1, certains voient le problème lié à une hypoténuse trop petite.
• Pour le 2, l’inégalité triangulaire est très loin… mais le triangle n’est pas constructible.
• Pour le 3, de tête 10² + 5² = 125 et 11² = 121, donc 11,2² > 121 : ça fonctionne peut-être mais difficile d’en dire plus sans faire les calculs.
  La difficulté rencontrée ici pour les élèves consiste à réfléchir sur des approximations avec des carrés et en plus j’avais dit de ne pas « faire » les calculs... Je devrais plutôt dire « ne pas poser ».