espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > 2023-2025
curseur de certitude et triangle rectangle
mis à jour le 27/05/2024
Une expérimentation pédagogique sur le thème "favoriser l'esprit critique" expérimentée dans deux classes de 4e.
mots clés : TraAM, esprit critique, Pythagore, certitude

1. INTRODUCTION
Le triangle est-il rectangle ?
En début de 4ème, les élèves pensent que la seule manière de répondre à cette question est de construire le triangle. Ils ont donc du mal à voir l’intérêt d’utiliser le théorème de Pythagore (réciproque et contraposée).
Donc l’objectif de l’activité est de faire douter les élèves sur leur démarche de construction, d’arriver à un débat entre les élèves sur leur moyen de vérification (utilisation de l’équerre).
Le premier objectif de l’activité est de faire douter les élèves sur leur démarche de construction et d’arriver à un débat entre eux sur leur moyen de vérification (utilisation de l’équerre).
Enfin, l’activité doit aussi permettre de mettre en évidence la différence entre la « géométrie dessinée » et la « géométrie abstraite ».
Pour cela, j’ai repris un exercice (issu du livre « Des Maths ensemble et pour chacun » niveau 4ème) que je proposais les années passées en ajoutant une contrainte supplémentaire. Pour forcer les élèves à avoir un esprit critique sur leur réponse, ils devaient donner leur degré de certitude à l’aide d’un curseur de confiance.
2. PRINCIPE DE L’ACTIVITE
Version 1 : (issu du livre « Des Maths ensemble et pour chacun » niveau 4ème)
Version 2 :
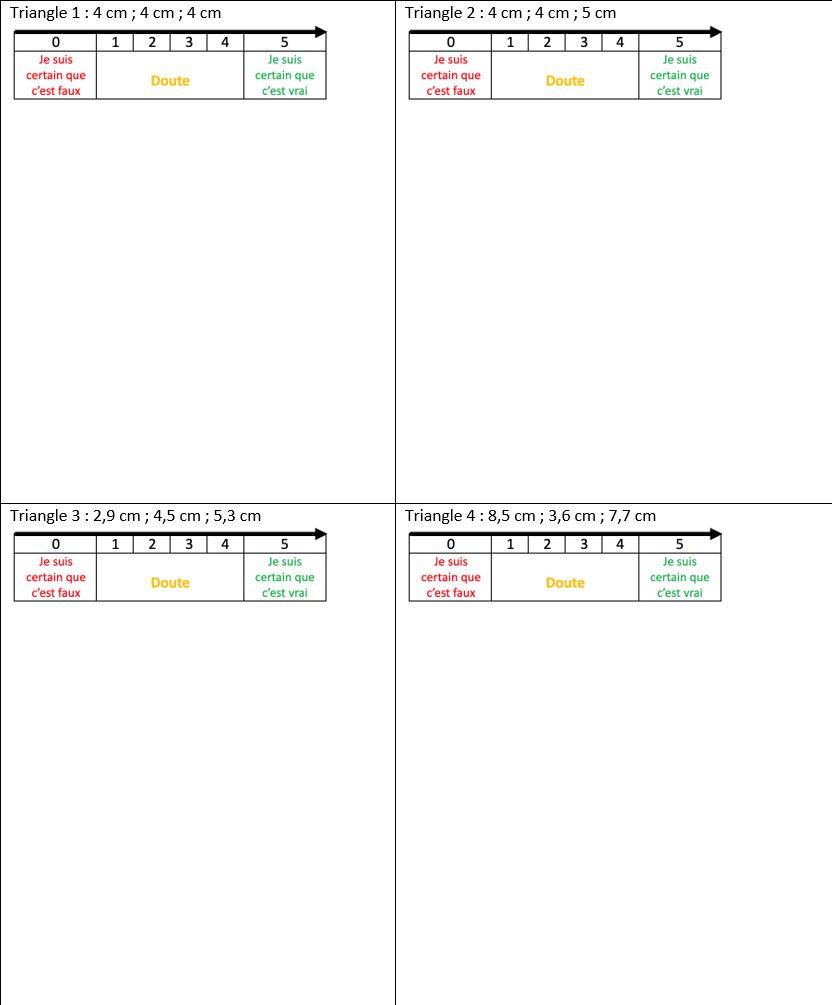
Pour chacun des cas suivants, on se demande si l’on a un triangle rectangle.
Qu’en penses-tu ? Es-tu certain de ta réponse ? Pour illustrer ton degré de certitude, positionne-toi sur le « curseur de confiance » en mettant une croix dans l’une des cases de 0 à 5. Dans chaque cas, donne un argument à ta réponse.
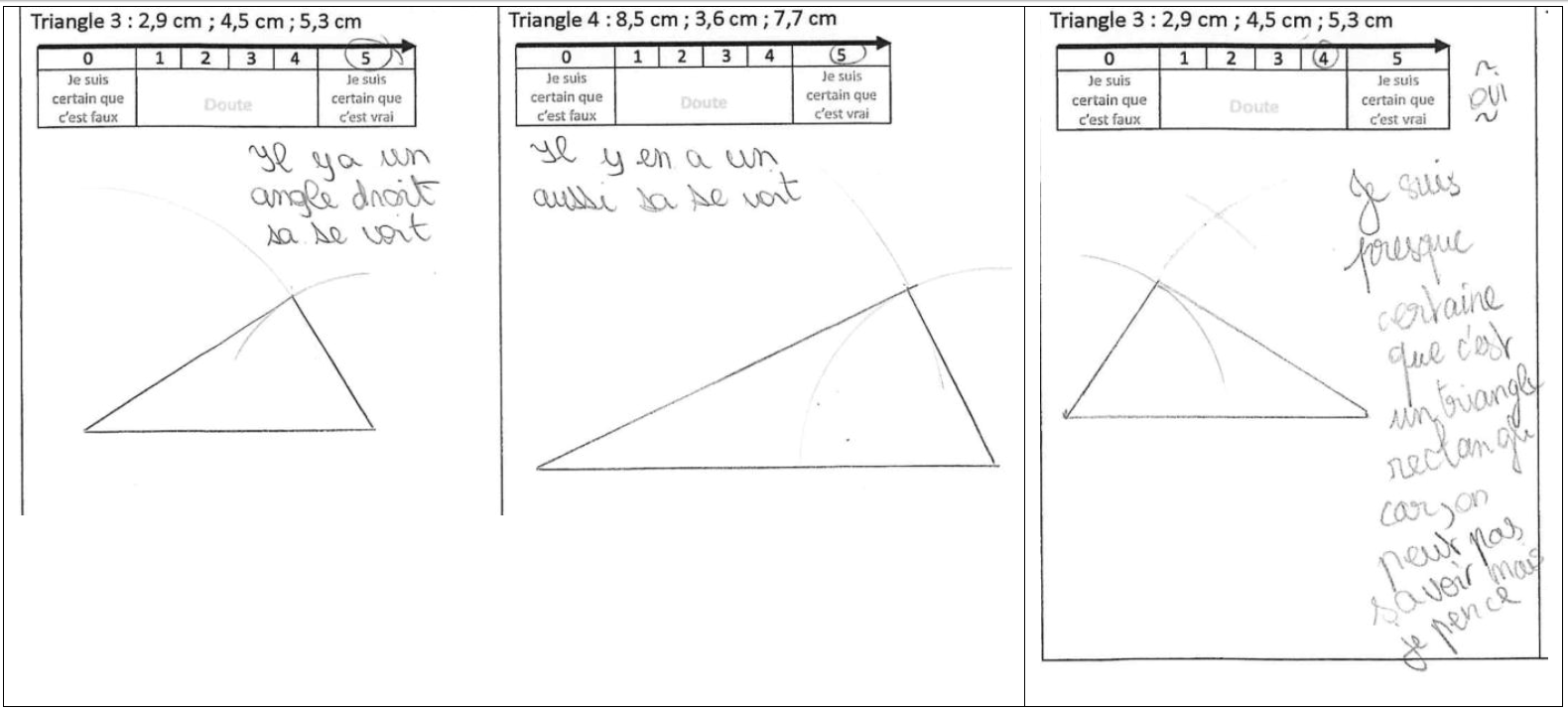
3. QUELQUES REPONSES D’ELEVES.
4. CONCLUSION DE L’ACTIVITE.
Une très large majorité des élèves s’est positionné sur le niveau 0 ou le niveau 5 avec donc beaucoup d’erreurs. L’objectif d’arriver à un débat sur la réponse à donner a donc été atteint et a permis de rendre nécessaire la découverte d’un nouvel outil mathématique : la réciproque ou la contraposée du théorème de Pythagore.
Enfin, concernant l’esprit critique, les positionnements des élèves montrent un manque de prise de recul. De plus, le fait de s’être positionné comme « certain » d’une réponse fausse accentue je pense, l’intérêt de la géométrie « abstraite » et les limites de la géométrie dessinée.
Voici quelques bilans d’élèves après avoir fait une autre séance sur la réciproque et la contraposée du théorème de Pythagore afin de pouvoir enfin savoir quels étaient les triangles rectangles.
Arnaud Boulay, enseignant au collège Suzanne Bouteloup - Mayet (72)
information(s) pédagogique(s)
niveau : tous niveaux
type pédagogique :
public visé : non précisé
contexte d'usage :
référence aux programmes :
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA