espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > 2023-2025
échelle de certitude et calcul littéral
mis à jour le 17/04/2024
mots clés : TraAM, esprit critique, calcul littéral

Testée dans une classe de 5e au collège Pierre Dubois.
Introduction
L’activité proposée s’inscrit dans une volonté de développer l’esprit critique chez les élèves.
Le but premier est de renforcer chez les élèves la compréhension de l’exemple, du contre-exemple et de la nécessité de généraliser en testant des égalités. A travers plusieurs tests d’égalité, ils seront amenés à se poser plusieurs questions : un exemple ou un contre-exemple suffit-il ? A partir de combien de tests peut-on conclure ? …
Pour favoriser ce questionnement, ils devront se positionner sur une échelle de certitude, d’abord seul puis par groupe de 3 ou 4 ils devront se mettre d’accord.
Suite à une première activité, il m’a paru intéressant de prolonger en se questionnant sur la cohérence des réponses données par les élèves.
Principe de l'activité
Une égalité est donnée aux élèves.
- 1er temps : individuellement chaque élève teste l’égalité en choisissant 3 nombres.
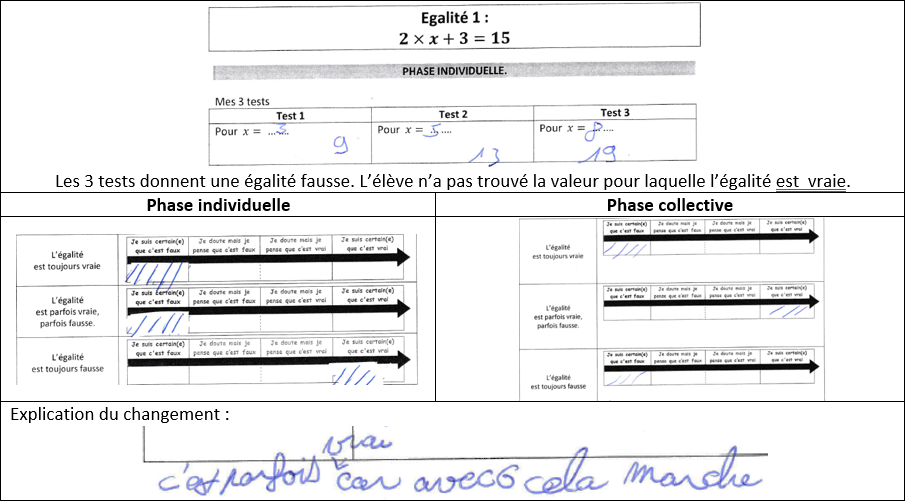
Exemple : 2×x+3=15 - 2ème temps : Chaque élève complète l’échelle de certitude pour chacune des 3 réponses possibles :
- 3ème temps : Ils comparent, argumentent et se mettent d’accord par groupe de 4, pour compléter de nouveau l’échelle de certitude. En cas de changement par rapport à la phase individuelle ils doivent expliquer les raisons de cette modification.
| L’égalité est toujours vraie. |  |
| L’égalité est parfois vraie, parfois fausse. |  |
| L’égalité est toujours fausse. |  |
Pour éviter que les erreurs de calcul viennent parasiter le but de l’activité, la calculatrice est autorisée.
Voici les égalités proposées :
| égalité | véracité | difficulté |
| Egalité 1: 2×x+3=15 | Parfois vraie parfois fausse | Peut-être trouvé facilement par les élèves. |
| Egalité 2 : 12×(3,2+1,6×x)=62,4 | Parfois vraie parfois fausse | Pas évident de trouver 1,25 pour l’égalité vraie |
| Egalité 3 : 2+5×(x-x)=2 | Toujours vraie | Démontrable |
| Egalité 4 : 3×8×x-4×6×x=2 | Toujours fausse | Démontrable |
| Egalité 5 : 2×(2×x+4)-10×x-7=13 | Toujours vraie | Non démontrable pour l’instant en 5ème (distributivité et simplification non vues) |
Quelques réponses d'élèves
Pourquoi ils ont changé de réponse ?
Voici quelques exemples des réponses des élèves et surtout les explications qu’ils donnent quand ils changent d’avis entre la phase individuelle et celle collective :
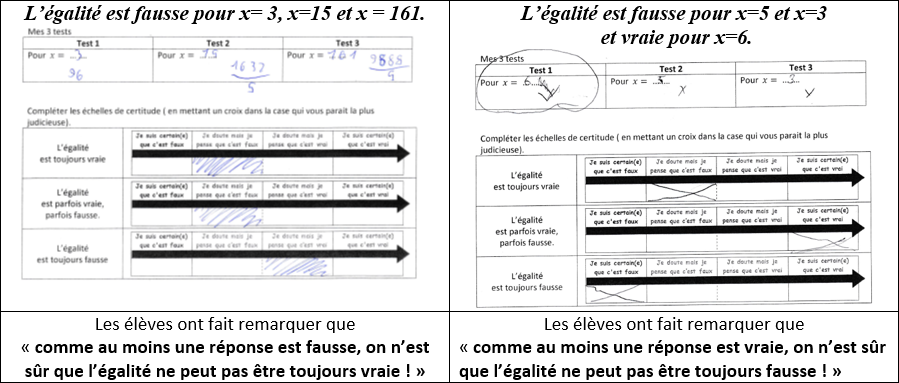
Des réponses incohérentes
Des élèves ont donné des réponses incohérentes. Elles ont été exploitées en classe :
Conclusion de l'activité
Après analyse des différentes égalités et des différentes réponses d’élèves la classe est arrivée aux conclusions suivantes :
- Un test d’égalité faux suffit pour affirmer que l’égalité n’est pas toujours vraie.
- Un test d’égalité vrai suffit pour affirmer que l’égalité n’est pas toujours fausse.
- Un test d’égalité vrai et un test faux suffisent pour être sûr que l’égalité est parfois vraie et parfois fausse.
- Pour prouver qu’une égalité est toujours vraie ou toujours fausse, il faudrait essayer tous les nombres, mais c’est impossible ! Il faut trouver une autre manière de faire sans essayer tous les nombres !
Damien Rivière, enseignant au collège Pierre Dubois – Laval (53)
information(s) pédagogique(s)
niveau : tous niveaux, Collèges tous niveaux, Cycle 4, 5ème
type pédagogique :
public visé : non précisé
contexte d'usage :
référence aux programmes :
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA