mathématiques

Première activité : la suite de Syracuse

Retrouver également la fiche sur la suite de syracuse en bas de page.
L’exercice est présenté comme tel et laissé à traiter par les élèves, de sorte qu’ils puissent construire (valider selon eux) eux-mêmes leur conjecture.

Lors de la séance, je passe vérifier le travail des élèves, car certains ne parviennent pas à revenir sur une série de 4 ; 2 ; 1, ce qui est souvent lié à une erreur de lecture de l’énoncé (ils utilisent régulièrement la mauvaise formule pour calculer u_n+1).

La conjecture de Syracuse étant émise, je ne rajoute rien sur le fait qu’il ne s’agisse que d’une conjecture, et qu’elle n’a pas été démontrée.

Les élèves sont ensuite invités à tester leur conjecture, pour la séance suivante, sur d’autres exemples, afin de la “valider”.

Quelques freins liés à l’activité

• Comme prévu, certains élèves sont gênés par le mode de génération de la suite (première situation ou la relation de récurrence peut changer selon le terme obtenu à l’itération précédente). Malgré tout, l’entraide et le fait de laisser les élèves en autonomie permet de venir aider les membres du groupe en ayant besoin :
• On pourrait penser que le travail se termine rapidement pour les éléments plus efficaces, mais la notion de conjecture demandée peut être “validée” par plusieurs choix de premiers termes de la suite. On peut par exemple proposer 100 comme premier terme, ou 27.
• Pour les situations que les élèves n’auraient pas réussies à terminer, un fichier tableur (Retrouver également la fiche en bas de page.) est préparé, pour s’éviter les calculs intermédiaires, et “valider la conjecture”.

Deuxième activité : suite de nombres premiers

Retrouver également la fiche sur la suite de nombres premiers en bas de page.
La deuxième activité est un exercice adapté du baccalauréat, lors duquel on demande de vérifier si les termes de la suite définie de façon explicite, pour tout entier naturel non nul, u_n = n²-n+41 sont premiers.

L’activité leur étant donné comme tel, les élèves ont, à leur disposition, un tableau de nombre premiers (Retrouver également la fiche en bas de page) projeté sur le tableau. A eux de se débrouiller pour voir si l’affirmation est valable ou non.

Lors de cette activité, deux clans se créent dans la classe :

• Un groupe “lâche l’affaire” et considère que le nombre de tests réalisés suffit pour conclure que l’affirmation est vraie
• Un autre groupe persévère et vérifie que l’assertion est fausse pour n = 41.

En fin de séance, j’explique comment on aurait pu vérifier que l’affirmation n’avait aucune chance d’être valable pour n = 41, et demande aux élèves pour quels “type d’entiers” elle n’est évidemment pas valable (les multiples de 41).

Troisième activité : secteurs de disque

Retrouver également la fiche sur l'activité secteurs de disque en bas de page.
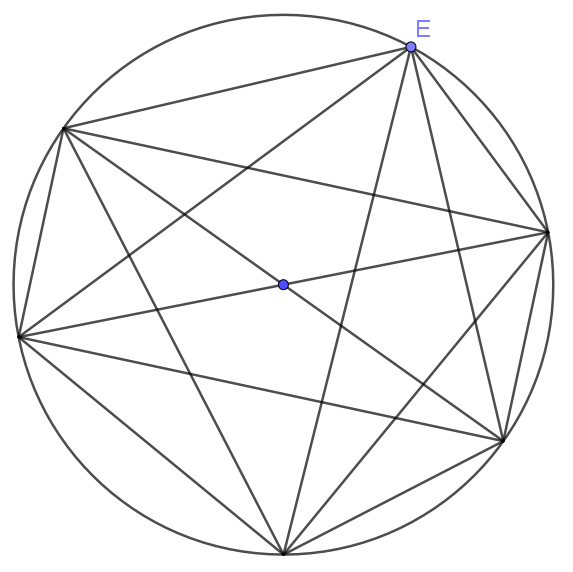
L’activité en question peut être travaillée au collège ou au lycée, avec des consignes différentes, et des objectifs différents. L’énoncé, en apparence très simple, permet d’obtenir une conjecture évidente, et sur laquelle l’ensemble des groupes classe s’entend, mais qui s’avère fausse.

Je laisse volontairement les élèves faire leur propre conjecture, et l’ensemble du groupe classe est unanime : le nombre de secteurs de disques se calcule ainsi pour n points placés, il y a 2^n-1 secteurs de disque.

Précision : les élèves entrevoient plutôt une relation de récurrence (à chaque point supplémentaire placé, on double le nombre de secteurs de disque).

Après établissement de la conjecture sur le nombre de secteurs de disque, je demande aux élèves de compter ce nombre de secteurs en rajoutant un point. Certains en comptent 32, d’autres 31... Les élèves en ayant compté 31 secteurs sont persuadés d’avoir mal compté, ce qui leur est confirmé par les autres. Ils recomptent et retrouvent 31...

Le fichier joint est préparé pour compter de façon claire le nombre de secteurs de disque obtenus pour 6 points. Il sera projeté pour que l’on puisse compter ensemble et vérifier que la conjecture est fausse. Je redemande alors aux élèves ayant compté 32 secteurs de vérifier, afin de se mettre tous en accord sur 31 secteurs.

Bilan

Sur l’ensemble des activités, et des conjectures menées, on réalise un bilan avec la classe :

• la première reste à l’état de conjecture que je précise s’appeler la conjecture de Syracuse ;
• la deuxième s’avère fausse, preuve à l’appui ;
• la troisième s’avère également fausse (par l’expérimentation).

J’en profite pour insister sur le manque de véracité d’une conjecture, et qu’une démonstration est nécessaire.

Pour ce qui est de la troisième activité, une formule est proposée au groupe, qui coïncide avec les puissances de 2, mais qui ne coïncide plus dès que n>5 : pour tout entier naturel strictement positif, le nombre de secteurs pour n points placés sur le cercle est : .           

Une démonstration de la formule proposée (Retrouver également la fiche en bas de page). Pour ma part, je n’ai pas insisté sur la démonstration de cette formule, qui est clairement hors programme, mais qui peut éventuellement être travaillée, je pense, dans l’option Maths Expertes. Il a seulement été précisé que l’on pouvait le prouver avec un travail de dénombrement, mais qui n’est pas actuellement à notre portée. Pour valider la formule, nous l’avons seulement testée en classe avec un émulateur de calculatrice projeté au tableau. Je m’attendais à quelques réticences sur ce dernier point, imaginant que les élèves ne seraient pas convaincus par cette conclusion, mais ils l’ont visiblement bien acceptée.

Je profite également de cette étude pour montrer l’intérêt de la condition “non diamétralement opposés” notée dans l’activité (Retrouver également la fiche en bas de page.).

La poursuite de l’étude se fait par la démonstration de la monotonie de plusieurs suites (créée par conjecture, puis validée). Ces démonstrations semblent légitimes auprès des élèves, par l’ensemble de l’étude réalisée.

Bilan général

Pour les élèves

Bilan positif, les élèves se sont bien investis, et ont collaboré, en ayant malgré tout divergé sur leurs points de vue.

Pour l’enseignant

Bilan positif également, permettant de légitimer la notion de démonstration, notamment sur la monotonie des suites. Un frein reste à noter sur la maîtrise du calcul algébrique.

Malgré tout, l’objectif annoncé initialement est atteint : les élèves ont travaillé leur esprit critique, et se sont accordés à ce qu’une hypothèse devait être vérifiée par une démonstration.

Les activités proposées sont bien évidemment transférables au collège, avec un autre vocabulaire, mais demeurent accessibles à partir de la classe de 4ème, à condition d’avoir commencé le calcul littéral, et d’avoir traité les nombres premiers<.