mathématiques

2. PRINCIPE DE L’ACTIVITE

La semaine précédente, nous avions découvert les propriétés caractéristiques de la médiatrice, fait des exercices de construction et d’application pour trouver un ou des points équidistants des extrémités de segments.
Pour que l’activité proposée n’apparaisse pas comme une application directe de la leçon, j’ai laissé passer une semaine sans reparler de la médiatrice…

Dans les deux pages suivantes, on trouvera les fichiers élèves en deux parties.

Document 1 : Introduction et énoncé

Document 2 : Fiche de construction
 

A ton avis, est-ce toujours possible ?
 

3. MISE EN OEUVRE

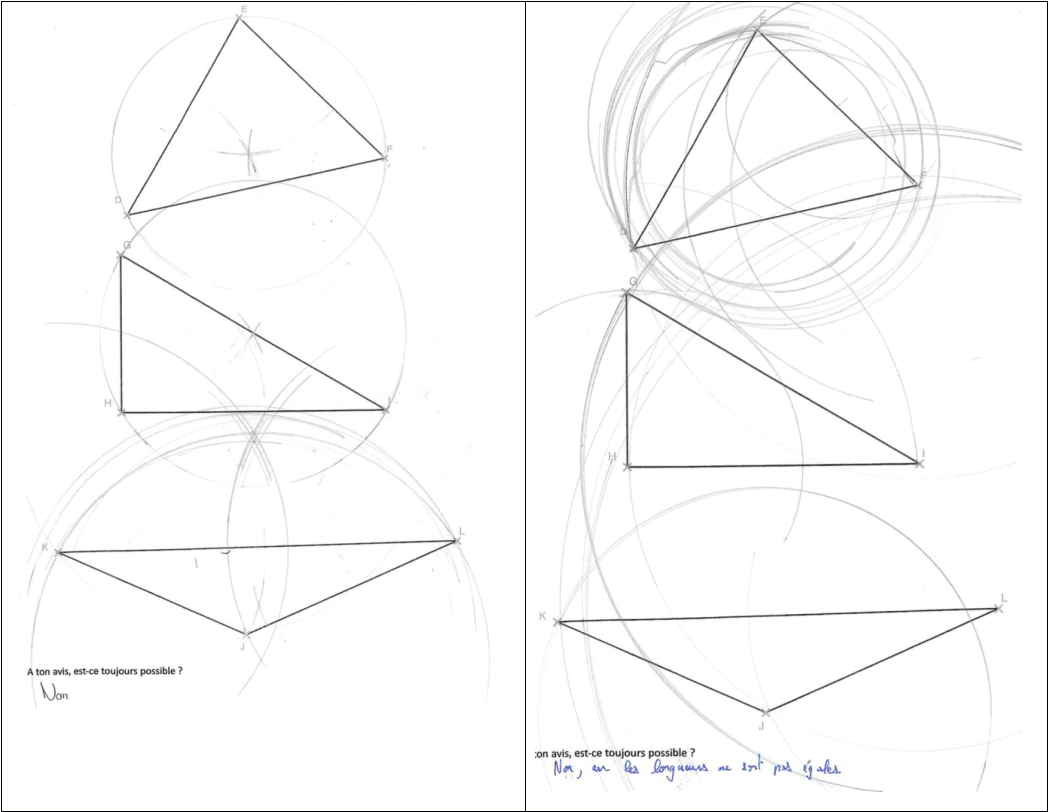
J’ai présenté cette activité sous la forme d’un défi. Les élèves avaient 10 minutes pour essayer de construire les trois cercles. Si un élève y arrivait, il devait immédiatement lever la main pour que je note le temps.

Dans les deux classes de 6ème, aucun élève n’a réussi à construire les trois cercles.
Avant de ramasser les feuilles pour les scanner, j’ai demandé aux élèves de répondre à la question : « A ton avis, est-ce toujours possible de construire un cercle passant par les trois sommets d’un triangle ? »

36 élèves sur 38 ont répondu « non » à cette question !
Les deux élèves qui ont répondu « oui » n’avaient pas réussi à construire les cercles.
 

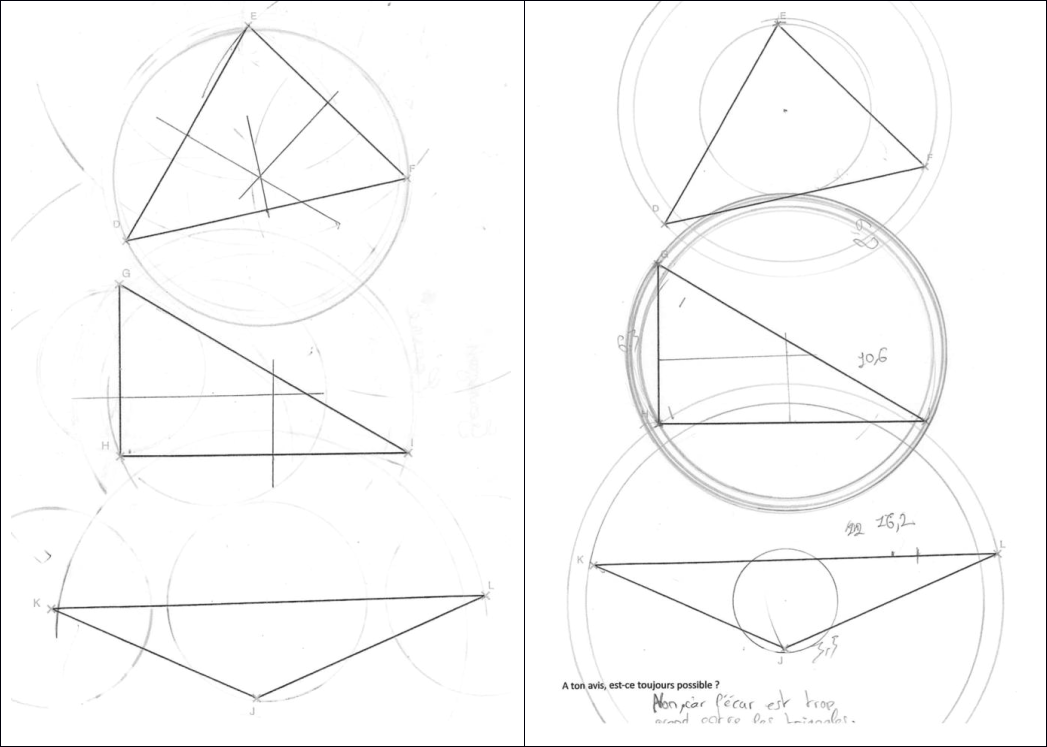
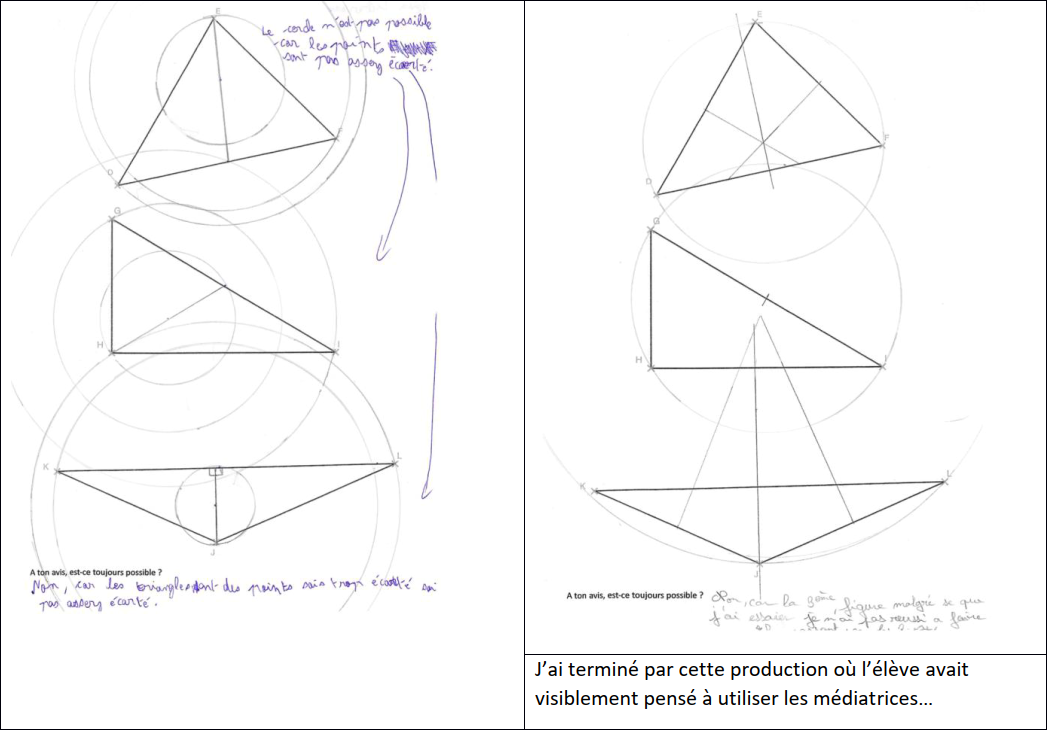
4. QUELQUES EXEMPLES D'ELEVES

5. BILAN ET CONCLUSION DE L’ACTIVITE.

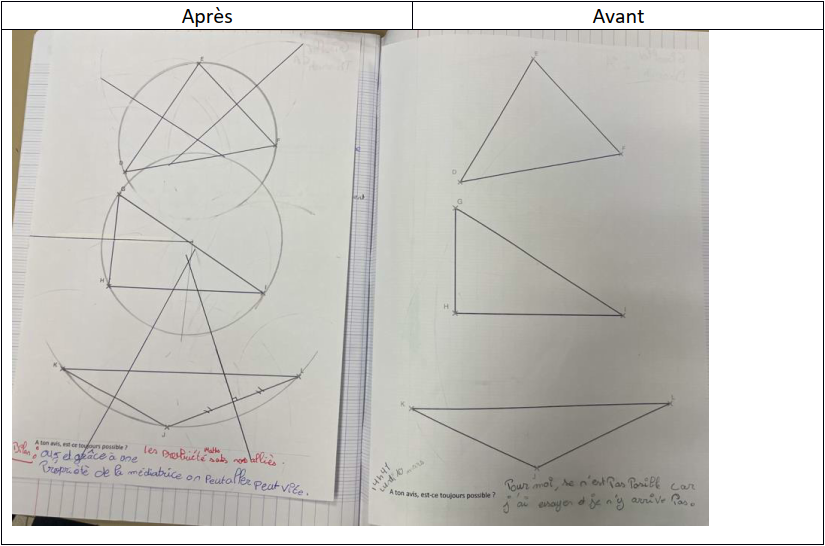
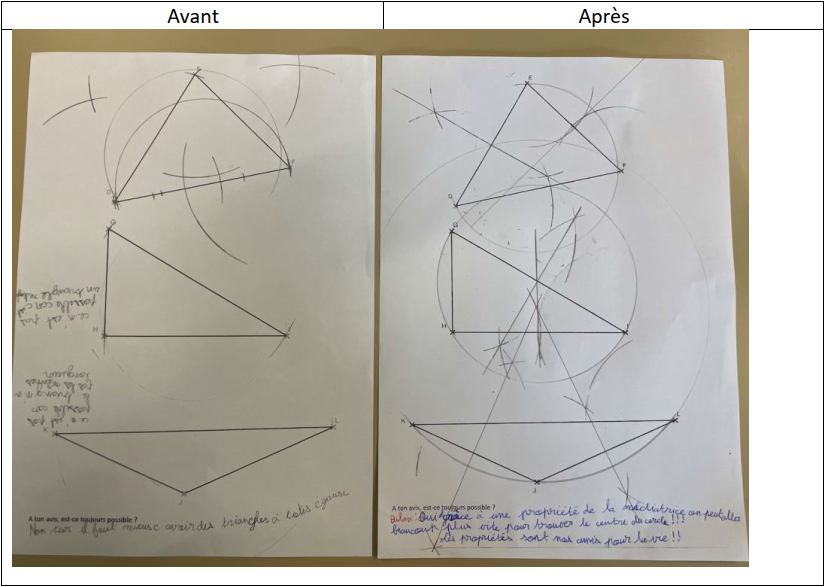
Lors de la séance suivante, j’ai projeté des productions pour illustrer différentes démarches puis je suis revenu sur les 36 « non » sur 38 en disant qu’ils se trompaient, qu’aucun élève n’avait réussi le défi en 10 min… alors que c’était possible en moins de trois minutes ! Et alors que les élèves étaient très étonnés, j’ai annoncé qu’il y avait une astuce et surtout qu’elle était dans le cahier de leçon… Cette fois, plusieurs élèves ont pensé à la médiatrice.
Grâce à une caméra/visualiseur, j’ai montré la manière de faire pour le premier triangle puis j’ai redistribué la feuille avec les trois triangles pour que les élèves puissent se rendre compte de la supériorité de cette méthode.
Voici deux photos (avant / après) pour illustrer l’apport de la propriété de la médiatrice :

Enfin, pour insister sur l’utilité et l’importance de connaître les propriétés mathématiques, nous sommes arrivés à une phrase que les élèves devaient compléter :
« Les propriétés mathématiques sont nos … » amies/ alliées/…
J’ai beaucoup aimé la réponse de cet élève et j’y fais référence lorsque nous rencontrons de nouvelles propriétés :