mathématiques

2. MISE EN PLACE EN CLASSE.

Il nous parait important de prendre l’habitude, dès le début de l’année, de montrer des travaux d’élèves pour travailler sur le fond et la forme de leurs productions, en utilisant des photos de leurs travaux.
Si au départ pour mettre en confiance il ne s’agit que des travaux des volontaires très rapidement, ce sont des travaux choisis qui sont projetés avec l’accord de leurs auteurs. Avec la pratique les élèves sont de moins en moins réticents.
Dans différentes situations et sur différentes questions, il est demandé aux élèves de critiquer les écrits proposés. Il est précisé que critiquer c’est donner les points positifs des documents ainsi que ceux qui leur posent problème.
Nous nous sommes attachés à mettre en exergue les remarques qui ont été faites par les élèves lors de la correction.
 

3. DEUX EXEMPLES DE PRODUCTIONS.

Exemple 1 - Sur la forme

Cet exemple intervient après plusieurs séances où des écrits d’élèves ont été projetés afin de construire ensemble les attendus d’une solution rédigée.
Il n’est au départ pas question de savoir si la réponse est juste ou fausse, mais de s’interroger sur la présentation proposée : est-elle accessible ? Est-elle compréhensible ?

Enoncé

Biscotte a construit un château de cartes à 3 étages comme sur l’image ci-contre:
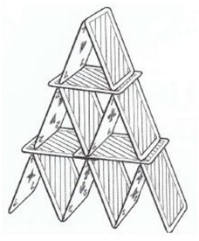
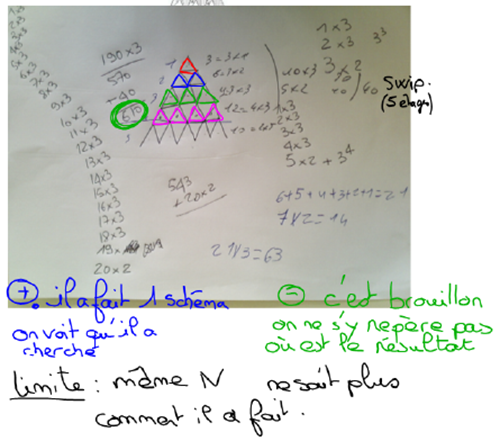
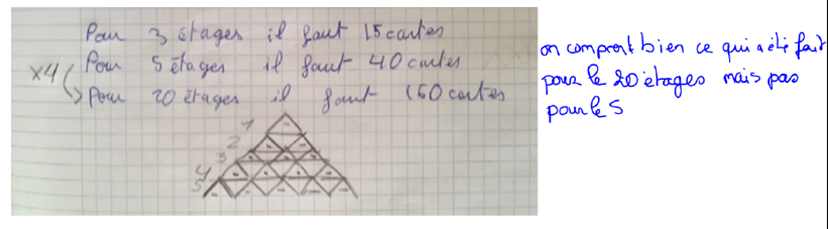
Swip a construit un château de 5 étages sur le même modèle. Combien a-t-elle utilisé de cartes ?
Flocon a construit un château de 20 étages sur le même modèle. Combien a-t-elle utilisé de cartes ?

Productions d’élèves et les critiques émises :






A la fin, les élèves s’accordent :

• sur l’utilité de faire un schéma et de laisser une trace claire du raisonnement sur celui-ci ;
• sur la nécessité de présenter correctement les calculs après avoir cherché.
   

Exemple 2 - Sur le fond

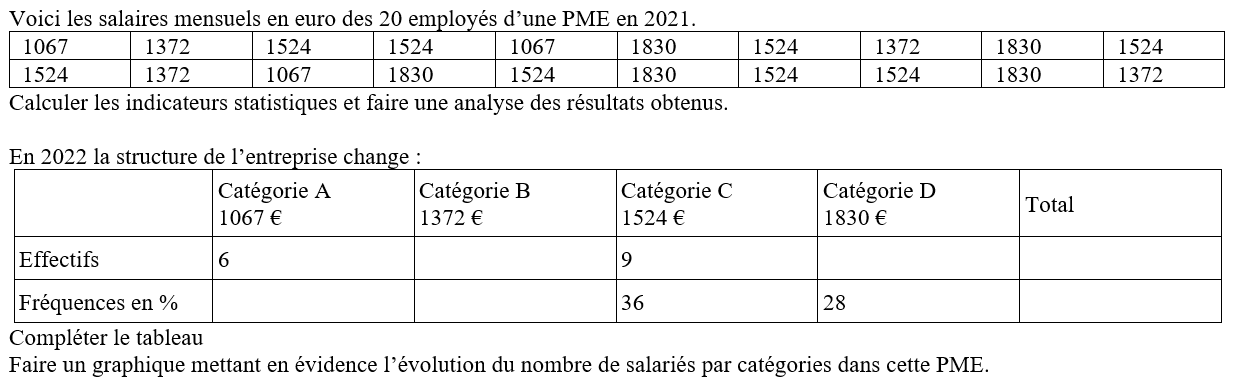
Enoncé

Compléter le tableau
Faire un graphique mettant en évidence l’évolution du nombre de salariés par catégories dans cette PME.

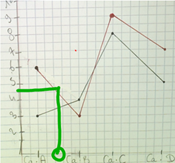
Productions
Six graphiques d’élèves sont projetés au tableau. Il est demandé de les critiquer.
Le travail se fait principalement à l’oral et seuls quelques commentaires sont notés au tableau.
Voici quelques critiques d’élèves et certaines remarques ou certains compléments que j’ai pu apporter.

Discret ou continue ?
 

Continue	Discret

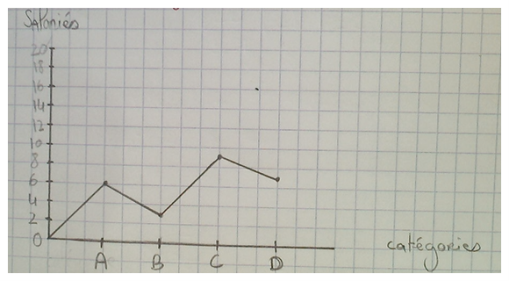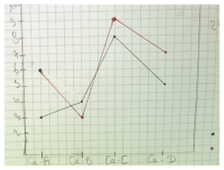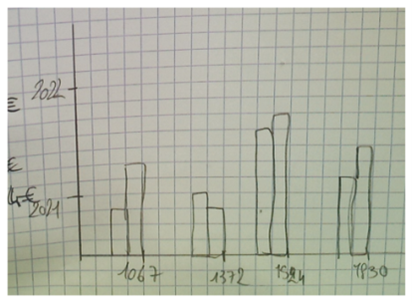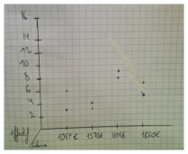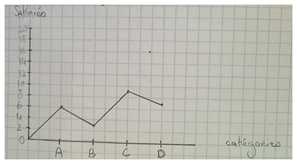
Elève 1 : « Il y a des graphiques avec des points reliés et d’autres où ils ont oublié de relier, du coup on voit moins bien »
Elève 2 : « oui, mais quand on trace jusqu’à l’axe des abscisses on voit bien aussi ? »

Compléments apportés :
J’ai mis en évidence qu’il s’agissait d’un caractère discret et qu’il n’était pas mathématiquement correct de tracer une ligne brisée.

Elève 3 : « dans ce cas il vaut mieux faire les barres pour mieux voir »
Quantitatif et qualitatif


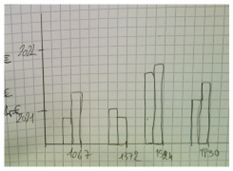
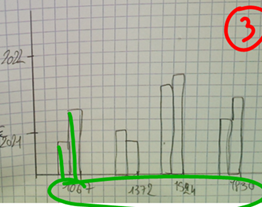
Elève 1 : « sur certains graphiques ils se sont trompés, ils n’ont pas mis de nombres sur l’axe des abscisses, ils ont mis des lettres ».

Elève 2 : « Ceux qui ont utilisé des nombres n’ont pas mis le bon écartement entre les nombres »

Il y a un vrai débat autour de cette notion d’échelle.
Doit-on respecter l’échelle dans cet exercice ?


Compléments apportés :
Des précisions sont apportées sur le caractère quantitatif ou qualitatif. Je nuance la différence entre ces 2 types de caractères en admettant (peut-être à tort) que dans cet exercice 1067 € peut être considéré comme qualitatif si on l’associe à la catégorie A, mais aussi comme un caractère quantitatif notamment quand on calcule la moyenne.

Un ou 2 graphiques ?


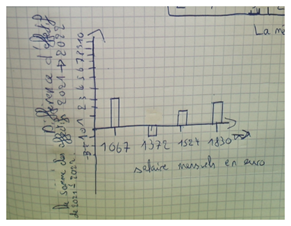
Elève 1 : « il s’est trompé, il a fait qu’une année ! »

Elève 2 : « en plus il a mis des salaires négatifs »

L’élève qui a fait ce graphique explique qu’il a travaillé en utilisant uniquement la variation entre les 2 années !

Les élèves sont en désaccord sur la pertinence de ce graphique, certains pensent que cela permet de mieux voir l’évolution et d’autres pensent que l’on voit moins bien. A-t-on besoin d’avoir une réponse tranchée ?
 

4. CONCLUSION.

Au fur et à mesure, les élèves comprennent et savent mettre en évidence ce qui est positif et ce qui est négatif dans la production proposée au tableau. Les analyses des élèves sont de plus en plus précises : on passe de « c’est bien » ou « c’est faux » ou « j’ai pas fait pareil » … à « c’est bien car … », « c’est faux car … » pour aller jusqu’à « Ce qui est bien c’est … par contre il aurait peut-être été mieux de … ». Les commentaires des élèves sont de plus en plus constructifs. Demander aux élèves de donner les remarques sous forme de questions peut permettre à l’auteur de l’écrit d’être dans l’échange et de moins se sentir jugé.

Ce type de pratique permet d’appréhender ce que signifie « critiquer » en mathématiques. On peut construire une correction commune, dans laquelle tous les éléments intéressants des productions peuvent être conservés ou améliorés et ceux qui posent problème sont corrigés. Cette manière de faire permet de réellement impliquer les élèves dans la correction, de valoriser les différentes méthodes et de déculpabiliser les élèves face à leurs erreurs.
Il s’agit au quotidien de petites gouttes d’esprit critique qui deviendront ruisseau, puis rivière et peut être un jour fleuve.