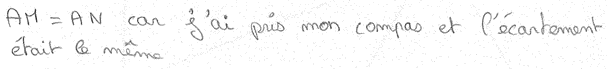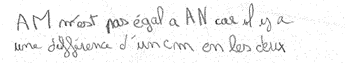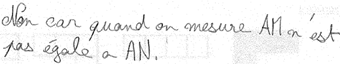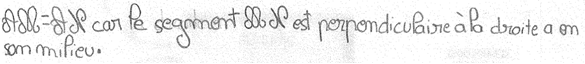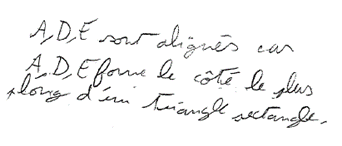mathématiques

espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > 2023-2025

... ou pas ?

mis à jour le 27/05/2025

Vous pensez que c'est vrai ? ... ou pas ?

mots clés : TraAM, Esprit critique, géométrie, démonstration, débat

Les objectifs

Un des objectifs de cette suite d'activités géométriques est d'aider les élèves à acquérir un état d'esprit, des pratiques et des connaissances favorisant le développement de leur esprit critique.

Écoute : Être attentif aux idées des autres et accepter le débat.
Curiosité : Avoir le désir d’apprendre et de comprendre.
Modestie : Reconnaître ses erreurs et savoir en tirer des leçons.
Lucidité : Distinguer ce que l'on sait avec certitude, ce que l'on suppose et ce que l'on ignore.

Un autre objectif, plus disciplinaire, est d'amener les élèves à percevoir les limites de la géométrie instrumentée afin de mieux comprendre les exigences de la géométrie déductive, qui repose sur des arguments fondés sur les définitions et les propriétés des figures.

Le protocole pour chaque activité

Une construction par semaine (le vendredi) sur trois semaines.

Voici les différentes étapes :

Présentation : le professeur décrit la figure et la dessine à main levée au tableau.
Construction – représenter : les élèves réalisent la figure eux-mêmes.
Questionnement : le professeur inscrit la question au tableau.
Réflexion – chercher : les élèves notent leurs idées et leurs observations.
Prise d'informations – communiquer : les élèves lisent ce qu'ils ont écrits.
Débat - raisonner : les élèves disent ce qu'ils pensent des arguments qu'ils ont entendus.
Conclusion ou pas.

Compte rendu d'expérience

Construction n°1

construction

Je remarque deux types d’argumentations, celles utilisant les mesures et celles utilisant des propriétés.

Argumentations utilisant les mesures
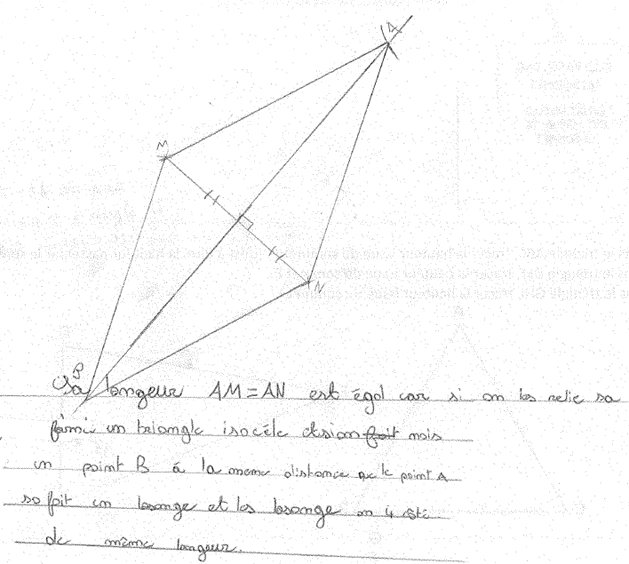
Élève A
productions d'élèves

Élève B

Élève C

Élève D

Je fais remarquer que, bien qu’ils aient suivi le même protocole de vérification, leurs conclusions sont différentes. Pour clarifier la situation, je demande alors à leurs voisins de vérifier les mesures et de confirmer ou d’infirmer les conclusions de leurs camarades.
Après vérification, les voisins des élèves C et D confirment les conclusions obtenues, tout en précisant que les longueurs sont « presque égales ».

D’autres élèves tentent des explications utilisant des propriétés ou d’autres figures
Élève E
productions d'élèves
Élève F

Élève G

Élève H

Élève I

Après la lecture de ces arguments, je demande à la classe s’il y en a une qui les a convaincus plus qu’une autre. Ceux des élèves F, G et H sont vite réfutés. Il y a plus de remarques pour ceux des élèves E et I.

Pour clore le débat, je demande à la classe de se positionner : les longueurs sont elles égales ou non ?
Une majorité d’élèves pensent qu’elles le sont.
Et là, je leur dis qu’on va passer à une autre activité … Des élèves me demandent alors qu’elle est la réponse.
Je leur réponds en souriant que je ne donnerai pas de réponse et on passe à l’autre activité.

Construction n°2

construction
Cette fois-ci, les arguments font tous appel à l’utilisation de la règle.

Les réflexions choisies
Élève A
productions d'élèves

Élève B

Élève C

La classe est plus partagée. Des élèves commencent à dire « on fait les mêmes vérifications et on arrive à des conclusions contraires » et me demandent : « est ce que cette fois, on aura une réponse ? »

Je leur explique qu’il existe deux sortes de géométries : la géométrie instrumentée et la géométrie déductive.
La géométrie instrumentée utilise la règle, le compas, l’équerre et le rapporteur pour vérifier, mais on arrive à une « presque » conclusion.
La géométrie déductive utilise des arguments qui se fondent sur les définitions et les propriétés des figures. Et je leur propose l’exemple de raisonnement suivant :

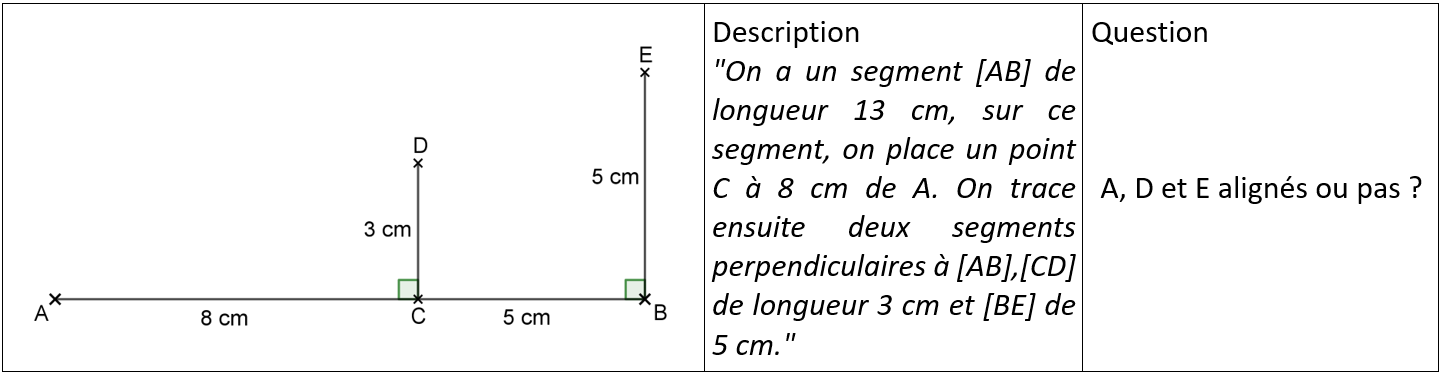
La démonstration proposée aux élèves
On suppose les points alignés.
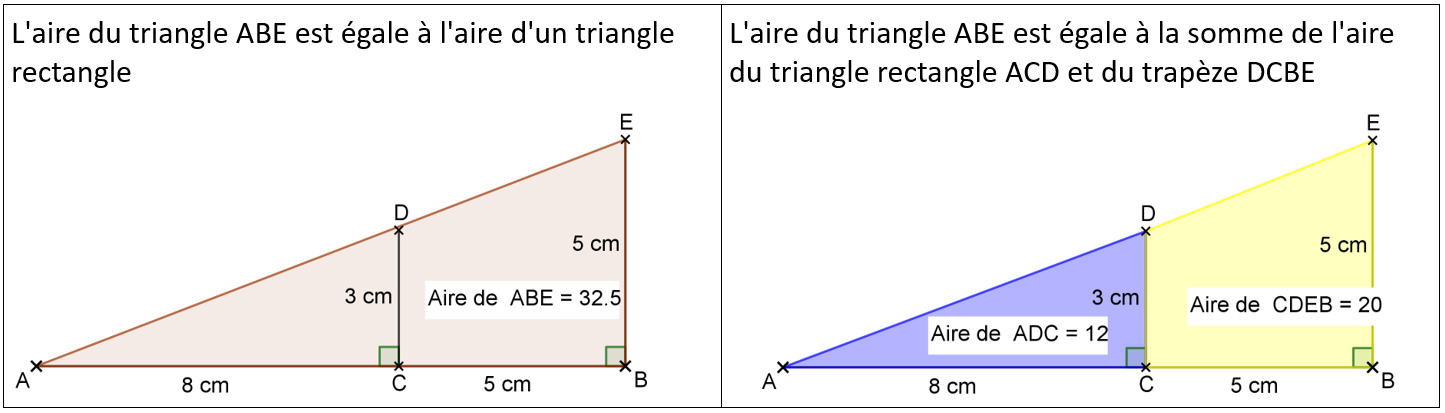
On va calculer l'aire du triangle ABE de deux manières.
correction
On arrive à la conclusion : 32,5=32
L’égalité est fausse. Donc le début de notre raisonnement est faux. Les points ne sont pas alignés.
La majorité est convaincue par le raisonnement.

Des élèves me demandent alors : pour la construction de la semaine dernière les longueurs sont égales ou pas ?
Par deux, je leur demande de chercher médiatrice dans un vieux livre de 6ème (Transmath édition 2005). Ils trouvent alors la définition et la propriété caractéristique de la médiatrice. Les longueurs sont bien égales.

Construction n°3

construction

On a :

Le OUI ou le NON
productions d'élèves

Le OUI et NON

Et la médiatrice ...

Les élèves sont convaincus par les derniers arguments.

En conclusion, je leur dis qu’on va continuer à faire deux géométries : une instrumentée et l’autre déductive.
Les figures que l’on va tracer, nous permettront de faire des observations que l’on appellera conjecture.

Par la suite la nécessité de démontrer est mieux comprise pas les élèves notamment lors de la découverte et la démonstration du point de concours des médiatrices d’un triangle, la semaine suivante.