espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > 2019-2021
la datation au carbone 14
mis à jour le 30/06/2020
mots clés : modélisation, simulation, exponentielle, TraAM
Niveaux : Première Générale Spécialité Mathématiques, Terminale STI2D Physique-Chimie et Mathématiques
Contexte :
En introduction du chapitre sur la fonction exponentielle, le but de cette activité est de faire émerger une nouvelle fonction et aussi mettre en place la notion d'équation différentielle. La fonction exponentielle n'est pas introduite par une formule ou une construction mais par une propriété mathématique.
L'exemple scientifique du carbone 14, connu au moins de nom par la plupart de élèves permet ici d'attirer leur curiosité (dans mon cas, une classe de terminale). L'activité nécessite l'acquisition de dés à 6 faces (10 dés par groupe au minimum).
On peut mettre l'accent sur la modélisation de la situation :
Durant la séance, une première approche de la loi des grands nombres peut être envisagé. Il est important d'avoir une grande quantité de dés lancés pour "lisser" le hasard et faire apparaitre l'évolution moyenne sous-jacente.
Contexte :
En introduction du chapitre sur la fonction exponentielle, le but de cette activité est de faire émerger une nouvelle fonction et aussi mettre en place la notion d'équation différentielle. La fonction exponentielle n'est pas introduite par une formule ou une construction mais par une propriété mathématique.
L'exemple scientifique du carbone 14, connu au moins de nom par la plupart de élèves permet ici d'attirer leur curiosité (dans mon cas, une classe de terminale). L'activité nécessite l'acquisition de dés à 6 faces (10 dés par groupe au minimum).
On peut mettre l'accent sur la modélisation de la situation :
- Un atome représenté par un dé
- Ne connaissant pas les mécanismes du changement d'état, on choisit un modèle probabiliste
- La proportion de changement est ici fixée à 1/6 de manière arbitraire. On pourra discuter en fin de séance du cas du carbone 14 (définir la valeur du coefficient grâce à des objets datés par une autre méthode : écrit, contexte, ...)
Durant la séance, une première approche de la loi des grands nombres peut être envisagé. Il est important d'avoir une grande quantité de dés lancés pour "lisser" le hasard et faire apparaitre l'évolution moyenne sous-jacente.
Activité : La datation au Carbone 14
Source : Wikipédia
La datation par le carbone 14, dite également datation par le radiocarbone ou datation par comptage du carbone 14 résiduel, est une méthode de datation radiométrique fondée sur la mesure de l'activité radiologique du carbone 14 (14C) contenu dans la matière organique dont on souhaite connaître l'âge absolu, c'est-à-dire le temps écoulé depuis la mort de l'organisme (animal ou végétal) qui le constitue.
Le domaine d'utilisation de cette méthode correspond à des âges absolus de quelques centaines d'années jusqu'à, et au plus, 50 000 ans. L'application de cette méthode à des événements anciens, tout particulièrement lorsque leur âge dépasse 6 000 ans (préhistoriques), a permis de les dater beaucoup plus précisément qu'auparavant. Elle a ainsi apporté un progrès significatif en archéologie et en paléoanthropologie.
En première approche, on peut considérer que tant qu'une plante ou un animal est vivant, son organisme échange du carbone avec son environnement si bien que le carbone qu'il contient aura la même proportion de 14C (carbone 14) que dans la biosphère.
La datation par le carbone 14 se fonde ainsi sur la présence dans tout organisme de radiocarbone en infime proportion (de l'ordre de 10-12 pour le rapport 14C/Ctotal). à partir de l'instant où un organisme meurt, la quantité de radiocarbone qu'il contient ainsi que son activité radiologique décroissent au cours du temps
Le domaine d'utilisation de cette méthode correspond à des âges absolus de quelques centaines d'années jusqu'à, et au plus, 50 000 ans. L'application de cette méthode à des événements anciens, tout particulièrement lorsque leur âge dépasse 6 000 ans (préhistoriques), a permis de les dater beaucoup plus précisément qu'auparavant. Elle a ainsi apporté un progrès significatif en archéologie et en paléoanthropologie.
En première approche, on peut considérer que tant qu'une plante ou un animal est vivant, son organisme échange du carbone avec son environnement si bien que le carbone qu'il contient aura la même proportion de 14C (carbone 14) que dans la biosphère.
La datation par le carbone 14 se fonde ainsi sur la présence dans tout organisme de radiocarbone en infime proportion (de l'ordre de 10-12 pour le rapport 14C/Ctotal). à partir de l'instant où un organisme meurt, la quantité de radiocarbone qu'il contient ainsi que son activité radiologique décroissent au cours du temps
Une Simulation avec des dés
Pour appréhender l'évolution de la quantité d'atome de Carbone 14, nous allons remplacer les atomes par des dés à 6 faces. A chaque étape, les dés marqués d'un " 1 " sont éliminées et ils représentent les atomes de Carbone 14 qui reviennent à l'état non radioactif de Carbone 12. Durant cette simulation, la probabilité de changement d'état est donc ici de 1/6.
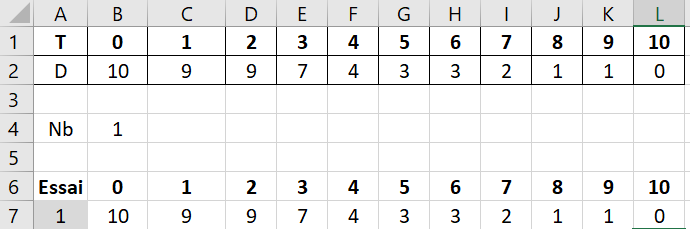
Activité de l'élève :
- Chaque élève reçoit un lot de 10 dès à 6 faces
- La règle de la simulation est la suivante :
- Lancer tous les dés disponibles
- Ecarter définitivement les dés affichants " 1 "
- Noter le nombre de dés restant dans le tableau ci-dessous
- Relancer ensuite les dés restants selon les mêmes règles
- Compléter le fichier Tableur du professeur pour rassembler les résultats de toutes la classe
Retour de mise en oeuvre : Avec des Terminales S (Lycée Touchard-Washington 2019-20)
| élève 1 | élève 2 |
 |  |
Dans un premier temps, chaque groupe effectue ses lancers et compare avec les voisins. L'ensemble des résultats est centralisé sur le poste professeur pour voir au fur et à mesure l'évolution de la courbe. On obtient le rendu suivant :
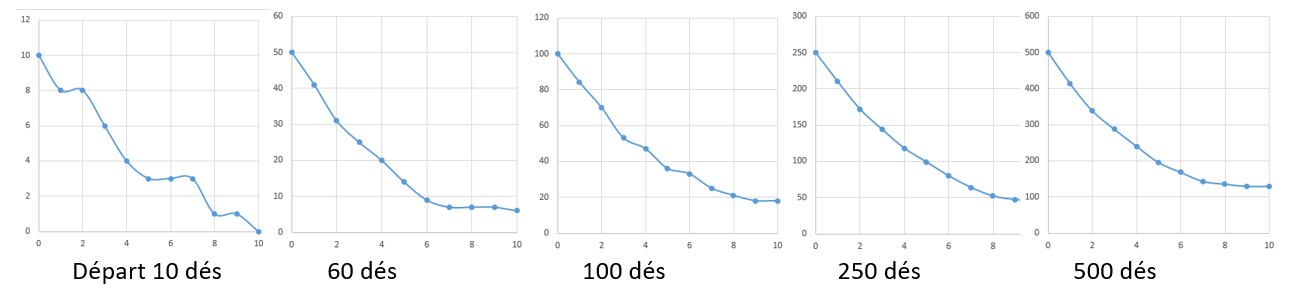
On observe le lissage de la courbe, c'est l'occasion de discuter avec les élèves de l'effet du hasard sur cette expérience. La première intuition des élèves est de faire appel aux suites et on pourra faire le lien plus tard avec la fonction exponentielle.

En commun, nous revenons sur le problème initial et en particulier sur la notion continue du temps. La courbe finale correspond-t-elle aux fonctions usuelles connues
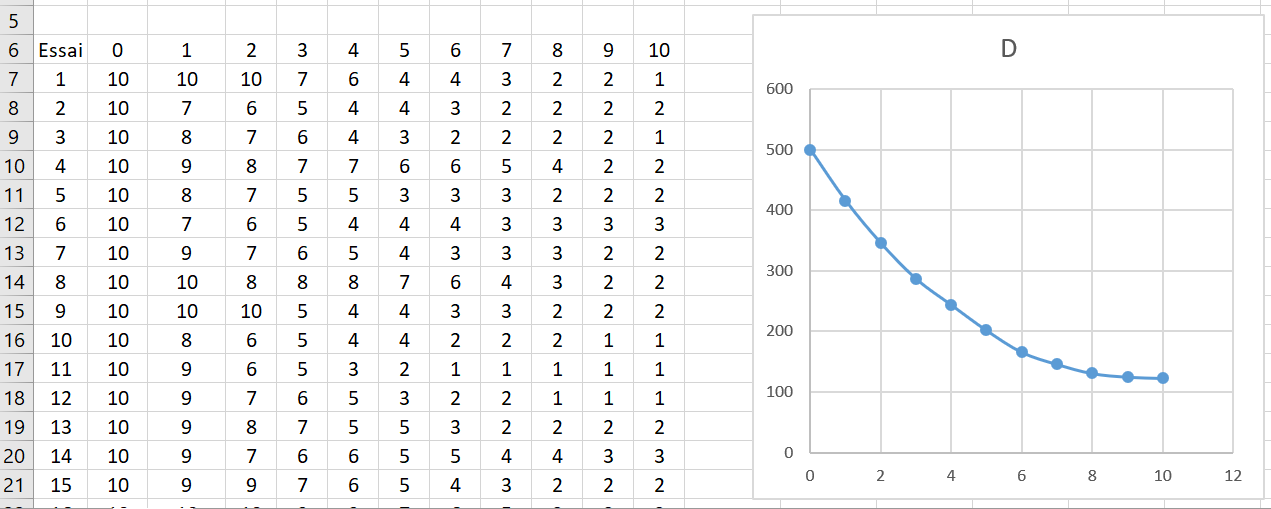
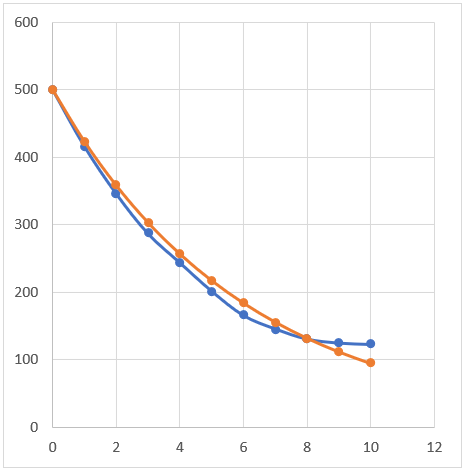
Mise en commun :
On va faire surgir les observations suivantes :
- La courbe est décroissante
- Elle ne correspond pas aux fonctions usuelles (-x, -x^2, …, 1/x)
- A chaque instant, 1/6 des dés peuvent disparaitre, on peut donc le traduire par ce fait ainsi : La fonction f recherchée devra vérifier :
.
Pour finir on peut voir qu'aucune fonction ne correspond (soit par les variations, soit par l'absence de valeur interdite). C'est donc le moment d'introduire l'équation différentielle en partant de l'idée des suites et en réduisant le pas de temps. A chaque instant 1/6 des dés disparaissent se traduit par
Pour simplifier la situation, on impose un coefficient plus simple que 1/6 avec la promesse de revenir dessus en fin de chapitre :

Hervé Diet, enseignant au lycée Touchard-Washington (Le Mans - 72)
information(s) pédagogique(s)
niveau : tous niveaux
type pédagogique :
public visé : non précisé
contexte d'usage :
référence aux programmes :
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA