espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > 2019-2021
le four solaire (une propriété de la parabole)
mis à jour le 09/06/2020
Lorsqu'on désire en faire plus avec des élèves de terminale qui se destinent à des études scientifiques.
mots clés : modélisation, parabole
Durée
5h réparties sur 5 semaines
Le contexte
L’activité qui suit a été proposée lors de l’atelier « Activité Interdisciplinaire » du lycée Aristide Briand de Saint-Nazaire. Cet atelier regroupe des élèves volontaires de terminale S qui se destinent à faire des études scientifiques exigeantes (classes préparatoires, licence de mathématiques, ...). Les séances ont lieu une fois par semaine. Les activités proposées font des ponts avec les autres domaines des sciences (SVT, sciences physiques, ...).
L’énoncé du problème
Dans un premier temps, une courte vidéo sur le four solaire de Font-Romeu est montrée aux élèves. Lors du débriefing les élèves conjecture la propriété suivante de la parabole.
« les rayons réfléchis issus de la rencontre entre une parabole et des rayons incidents parallèles à l’axe de symétrie de cette parabole convergent tous vers un point»
 | 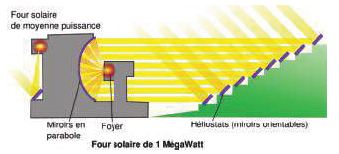 |
| D’après le film, que vous pourrez retrouver à l’adresse ci-dessous, un miroir parabolique est capable de concentrer les rayons du soleil en un point. https://www.youtube.com/watch?v=AzHAoGCSXM |  |
Déroulé de la séquence
Visionnage de la vidéo : 5 minutes
Discussion avec la classe et rédaction de la conjecture :10 minutes
Dessin sur papier : 15 minutes
Une feuille de papier est distribuée aux élèves sur laquelle se trouve la parabole d’équation y=x^2. Les élèves dessinent plusieurs rayons parallèles à l’axe de la parabole puis les rayons réfléchis correspondants plus ou moins précisément. Ils constatent qu’effectivement ces rayons réfléchis semblent converger vers une zone (un point pour les élèves les plus soigneux). Ce premier travail est l’occasion de discuter avec la classe du modèle choisi pour la réflexion du rayon incident sur la parabole. Un point est fait sur la réflexion d’un rayon sur une surface plane en prenant l’exemple de la boule de billard.
Aucun élève ne s’est lancé dans des calculs pour trouver les équations des rayons réfléchis. Ils ont tous fait des dessins approximatifs avec plus ou moins de succès !
Dessin sur Geogebra : 25 minutesAucun élève ne s’est lancé dans des calculs pour trouver les équations des rayons réfléchis. Ils ont tous fait des dessins approximatifs avec plus ou moins de succès !
Les élèves ont ensuite fait le même travail en utilisant le logiciel Geogebra. La mauvaise maîtrise par les élèves des différents outils de Geogebra et le manque de temps n’ont pas permis d’obtenir des fichiers très satisfaisants. L’animation proposée en annexe de ce document est une correction de ce travail. Elle a permis de poursuivre l’activité avec la classe car elle a servi de support visuel.
Démonstration : 4 h (réparties sur 4 semaines)Les autres séances ont été consacrées à la démonstration du résultat.
Dans un premier temps, les différentes étapes de cette démonstration ont été définies par les élèves. Pour cela, ils ont judicieusement suivi le cheminement d’un rayon quelconque.
Dans un deuxième temps, ils ont démontré ces différentes étapes en travaillant en autonomie (seul ou à plusieurs).
Un temps important aura été laissé aux élèves pour leurs recherches. Les démonstrations n’ont pas été faites à leur place mais régulièrement des synthèses étaient proposées par le professeur ainsi que des rappels des différents résultats de seconde ou première S nécessaires.
Dans un premier temps, les différentes étapes de cette démonstration ont été définies par les élèves. Pour cela, ils ont judicieusement suivi le cheminement d’un rayon quelconque.
Dans un deuxième temps, ils ont démontré ces différentes étapes en travaillant en autonomie (seul ou à plusieurs).
Un temps important aura été laissé aux élèves pour leurs recherches. Les démonstrations n’ont pas été faites à leur place mais régulièrement des synthèses étaient proposées par le professeur ainsi que des rappels des différents résultats de seconde ou première S nécessaires.
Synthèse de la démonstration faite par les élèves
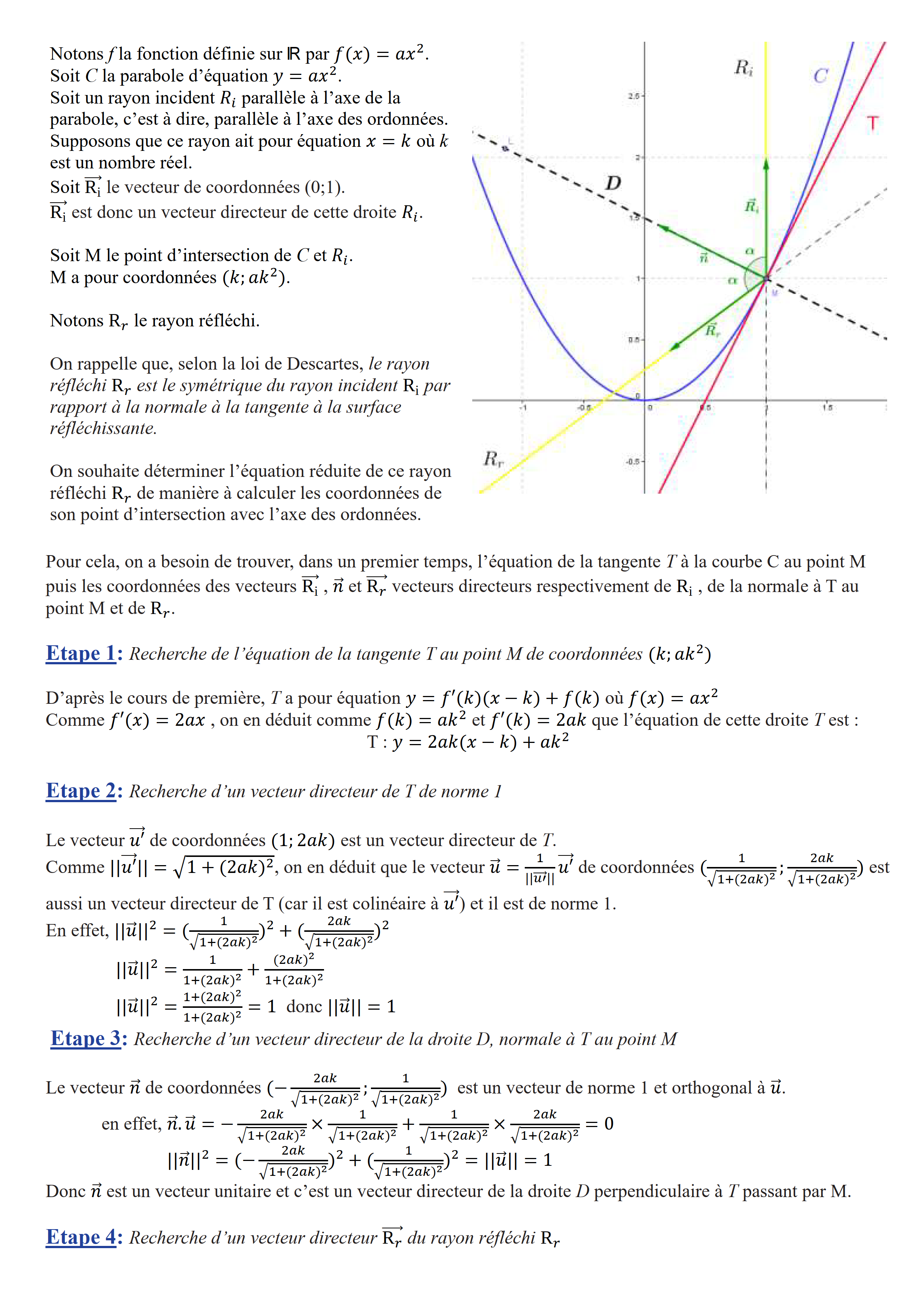
Objectif : Dans ce qui suit, on souhaite démontrer que les rayons réfléchis issus de la rencontre entre une parabole et des rayons incidents parallèles à l’axe de symétrie de cette parabole convergent tous vers un point.
 |  |
Yann Bertrand, enseignant au lycée Aristide Briand - Saint Nazaire (44)
information(s) pédagogique(s)
niveau : tous niveaux, Terminale S
type pédagogique :
public visé : non précisé
contexte d'usage :
référence aux programmes :
documents complémentaires
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA


