espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > 2019-2021
le projet tyrolienne
mis à jour le 30/06/2020
mots clés : modélisation, géométrie dans l'espace, équations paramétriques
Niveau : Terminale Générale Spécialité Mathématiques
Contexte :
Cette activité se place dans le cadre d'un temps de recherche. Le but est de présenter un cadre simple et compréhensible aux élèves et de leur laisser le choix des outils mathématiques et/ou informatiques nécessaires pour répondre à la problématique.
La présentation peut se faire sur place en se déplaçant dans le cours de l'établissement pour renforcer l'aspect réaliste de l'exercice.
L'activité peut se placer en début de chapitre pour faire apparaitre les notions ou à distance de la fin du chapitre pour remobiliser les connaissances acquises.
Ici, la modélisation se caractérise par le fait de simplifier la réalité pour pouvoir l'appréhender. Il sera alors pertinent d'insister sur la notion de retour vers le réel pour pouvoir valider les simplifications envisagées et le modèle choisi.
Contenu de la ressource :
- Un déroulement proposé.
- L'énoncé correspondant au Lycée Touchard-Washington du Mans (72).
- Une proposition de résolution.
Déroulé :
La fiche explicative est distribuée en premier pour laisser le temps à chaque élève de se l'approprier et de poser les questions nécessaires. Une fois ce temps passé, les élèves ont un temps de réflexion en petit groupe (2 ou 3 élèves) pour mettre en place une démarche, un plan d'attaque. Un temps en commun est prévu pour que chacun expose son plan d'action et ainsi aider les groupes peu inspirés. Ensuite les élèves sont renvoyés à leur feuille pour un temps de calculs et de mise en forme du projet. Il y aura, quelques séances plus tard, une présentation par chaque groupe de leurs conclusions.
La deuxième question (l'angle de descente) est accessible avec la notion de produit scalaire dans l'espace.
Le projet Tyrolienne
Pour faciliter les déplacements dans l'établissement, je vous propose de déposer un projet auprès du Conseil de la Vie Lycéenne pour installer des tyroliennes et traverser plus rapidement la cour :
- La voie 1 (verte), entre la salle des professeurs (1er étage du bâtiment F) et le rez-de-chaussée du bâtiment C
- La voie 2 (rouge), entre le 2ème étage du bâtiment C et le 1er étage du bâtiment A
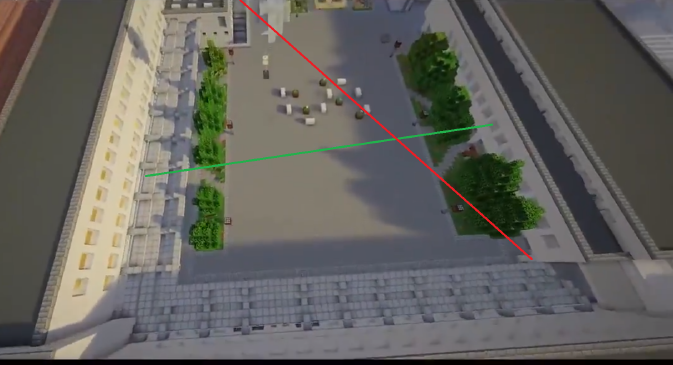
Reproduction sur MineCraft du Lycée par Mathis Le Métayer
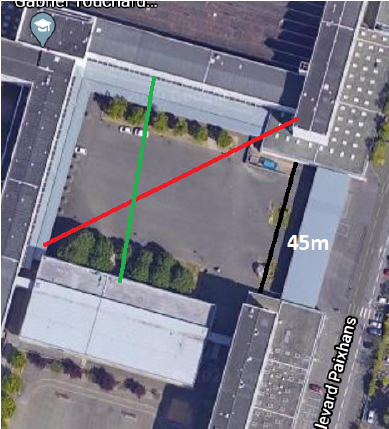 Source GoogleMaps | Pour que la « sécurité » soit assurée, il nous faut être sûr que :
Alors qu'en pensez-vous ? |
Retour de mise en œuvre : avec des Terminales S (Lycée Touchard-Washington 2019-20)
 Les premières propositions collent à la photo proposer, une vue de dessus qui donne un modélisation « plate » de la situation. Les élèves se rendent compte qu'ainsi ils peuvent pointer le point de croisement mais pas mesure la hauteur entre les deux câbles à ce moment. On a perdu une dimension | 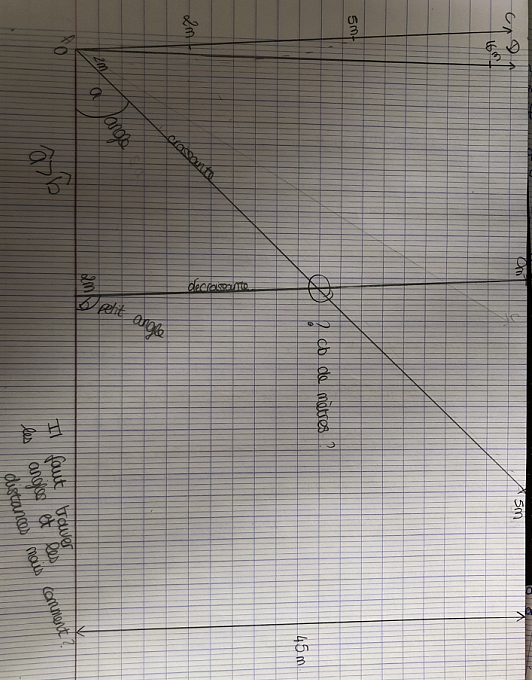 |
D'autre élèves proposent une vue en coupe qui permet d'avoir accès à la hauteur. La coupe choisie est naturelle par rapport aux axes de la cours, mais devrait plutôt se faire le long des voies des tyroliennes.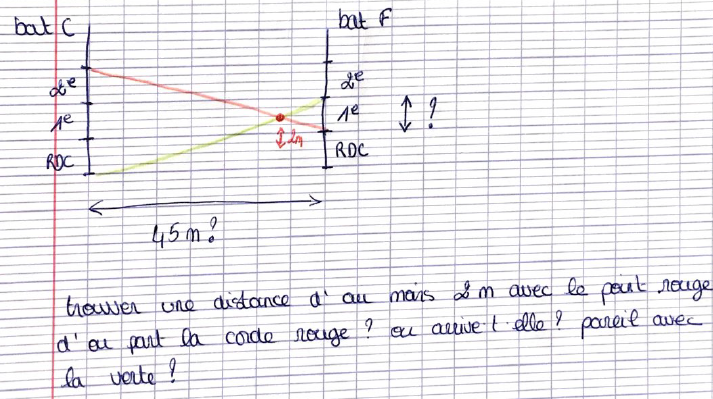 | 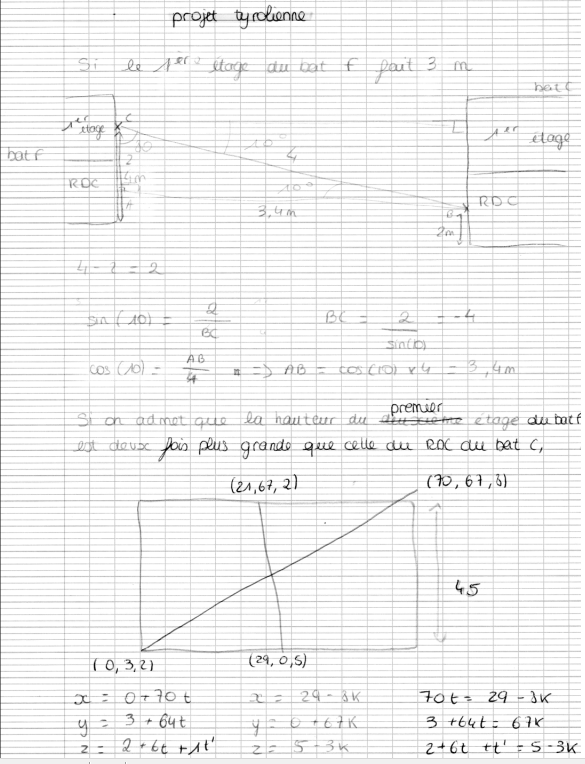 |
| Enfin d'autres élèves proposent une vision en trois dimensions qui rassemblent les trois axes. | 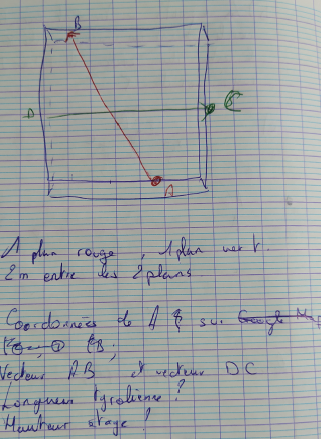 |
Réflexion collective en classe virtuelle :
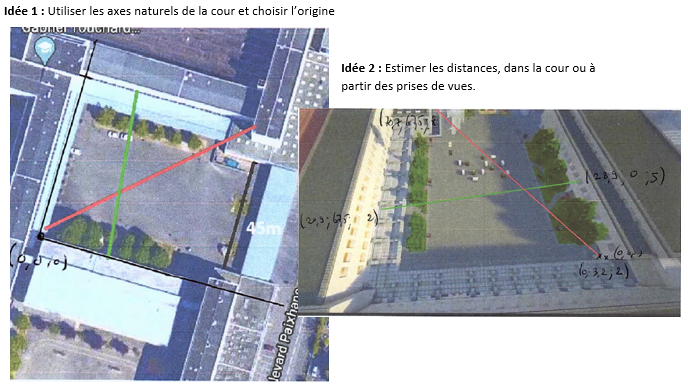
Une fois la modélisation choisie, les élèves sont repartis à leur feuille et leur ordinateur pour répondre aux questions posées.
A partir des coordonnées, on peut déterminer une représentation paramétrique de chaque tyrolienne. Pour la voie Verte :
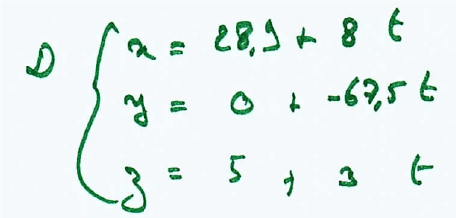
Pour la voie Rouge, on imagine un mur vertical au-dessus et donc on rajoute la partie bleue à la représentation

L'intersection de la voie Verte et du mur imaginaire, nous amène à la résolution d'un système. Les élèves peuvent le faire à la main, à la calculatrice ou avec les méthodes expertes (matrices)
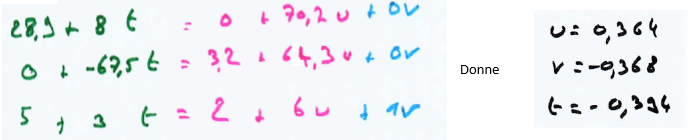
Une fois les paramètres trouvés, on récupère les deux points des voies, l'un au-dessus de l'autre pour voir leur distance

Le croisement est donc trop proche entre les deux voies.
Si la notion de produit scalaire est déjà vue, on peut traiter le problème de l'angle descente. Il faut rappeler que le produit scalaire entre deux vecteurs se calcule à partir des coordonnées ou de l'angle et des distances.
Pour la voie verte, on regarde donc le produit scalaire entre le vecteur directeur (8;-67,5; 3) et l'horizontale (8;-67,5; 0) :
Les normes sont :
Le produit scalaire des deux vecteurs vaut alors
On a ainsi un angle de descente dont le cosinus vaut :
On peut reproduire les mêmes calculs pour la voie Rouge, et on obtient environ 3,61° environ.
La pente rouge est donc aussi correcte.
Conclusion : On peut poser une des voies mais pas les deux. Enfin si le chef d'établissement est d'accord ! ! !
Hervé Diet, enseignant au lycée Touchard-Washington (Le Mans - 72)
information(s) pédagogique(s)
niveau : tous niveaux
type pédagogique :
public visé : non précisé
contexte d'usage :
référence aux programmes :
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA

